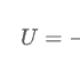• Süsteemid m lineaarvõrrandid koos n teadmata.
  Lineaarvõrrandite süsteemi lahendamine Kas selline numbrite komplekt ( x 1, x 2, ..., x n), kui see on süsteemi igasse võrrandisse asendatud, saadakse õige võrdsus.
  kus a ij, i = 1, ..., m; j = 1,…, n- süsteemi koefitsiendid;
  b i, i = 1, ..., m- tasuta liikmed;
  x j, j = 1, ..., n- teadmata.
  Ülaltoodud süsteemi saab kirjutada maatriksvormis: A X = B,
  
  
  
  
  kus ( A|B) Kas süsteemi peamine maatriks;
  A- laiendatud süsteemimaatriks;
  X- tundmatute veerg;
  B- tasuta liikmete veerg.
  Kui maatriks B ei ole nullmaatriks ∅, siis nimetatakse seda lineaarvõrrandite süsteemi ebahomogeenseks.
  Kui maatriks B= ∅, siis nimetatakse seda lineaarvõrrandite süsteemi homogeenseks. Homogeensel süsteemil on alati null (tühine) lahendus: x 1 = x 2 =…, x n = 0.
  Lineaarvõrrandite ühine süsteem Kas lineaarsete võrrandite süsteem, millel on lahendus.
  Lineaarsete võrrandite ebajärjekindel süsteem On lineaarsete võrrandite süsteem, millel pole lahendust.
  Kindel lineaarvõrrandite süsteem On lineaarsete võrrandite süsteem, millel on ainulaadne lahendus.
  Määratlemata lineaarvõrrandite süsteem Kas lineaarsete võrrandite süsteem, millel on lõpmatu lahendite komplekt.
• N tundmatu lineaarvõrrandi süsteemid
  Kui tundmatute arv on võrdne võrrandite arvuga, on maatriks ruut. Maatriksi determinanti nimetatakse lineaarsete võrrandite süsteemi peamiseks determinantiks ja seda tähistatakse sümboliga Δ.
  Crameri meetod süsteemide lahendamiseks n lineaarvõrrandid n teadmata.
  Crameri reegel.
  Kui peamine määraja lineaarvõrrandite süsteem ei ole võrdne nulliga, siis on süsteem järjepidev ja määratletud ning ainus lahendus arvutatakse Crameri valemite abil:
  kus Δ i - determinantid, mis on saadud süsteemi peamisest determinantist Δ asendades i veerg tasuta liikmeveeru kohta. ...
• N tundmatu lineaarvõrrandi süsteemid
  Kronecker - Capelli teoreem.
  
  
  Et antud lineaarvõrrandisüsteem oleks järjepidev, on vajalik ja piisav, et süsteemi maatriksi auaste oleks võrdne süsteemi laiendatud maatriksi auastmega, helistas (Α) = helistas (Α | B).
  Kui helises (Α) ≠ helises (Α | B), siis pole süsteemil kindlasti lahendusi.
  Kui helistas (Α) = helistas (Α | B), siis on võimalikud kaks juhtumit:
  1) helises (Α) = n(tundmatute arvuni) - lahendus on ainulaadne ja selle saab Crameri valemite abil;
  2) helises (?)< n - lahendusi on lõpmatult palju.
• Gaussi meetod lineaarvõrrandisüsteemide lahendamiseks
  
  
  Koostame laiendatud maatriksi ( A|B) antud koefitsientide süsteemist tundmatul ja paremal küljel.
  Gaussi meetod või tundmatute kõrvaldamise meetod seisneb laiendatud maatriksi ( A|B) elementaarsete teisenduste abil üle selle ridade diagonaalkujule (ülemisele kolmnurksele kujule). Tulles tagasi võrrandisüsteemi juurde, määratakse kõik tundmatud.
  TO elementaarsed muutused ridade kohal on järgmine:
  1) kahe rea vahetamine;
  2) stringi korrutamine muu arvuga kui 0;
  3) lisades stringile teise stringi, mis on korrutatud suvalise numbriga;
  4) nullnööri väljaviskamine.
  Laiendatud maatriks, vähendatud diagonaalkujule, vastab lineaarne süsteem, mis on samaväärne antud lahendusega, mille lahendamine pole keeruline. ...
• Homogeensete lineaarvõrrandite süsteem.
  Homogeenne süsteem näeb välja selline:
  
  see vastab maatriksvõrrandile A X = 0.
  1) Homogeenne süsteem on alati ühilduv, kuna r (A) = r (A | B), alati on nulllahendus (0, 0,…, 0).
  2) Selleks, et homogeenne süsteem on nulliväline lahendus, see on vajalik ja piisav r = r (A)< n , mis on võrdne Δ = 0.
  3) Kui r< n , siis meelega Δ = 0, siis tekivad vabad tundmatud c 1, c 2, ..., c n-r, süsteemil on mittetriviaalsed lahendused ja neid on lõpmatult palju.
  4) Üldlahendus X kl r< n saab maatriksi kujul kirjutada järgmiselt:
  X = c 1 X 1 + c 2 X 2 +… + c n-r X n-r,
  kus on lahendused X 1, X 2, ..., X n-r moodustavad põhilise otsuste süsteemi.
  5) Lahenduste põhisüsteemi saab homogeense süsteemi üldlahendusest:
  
  ,
  kui parameetrite väärtusi eeldatakse järjestikku (1, 0,…, 0), (0, 1,…, 0),…, (0, 0,…, 1).
  Üldlahenduse lagunemine lahenduste põhisüsteemi osas Kas üldlahenduse kirje põhisüsteemi kuuluvate lahenduste lineaarse kombinatsiooni kujul.
  Teoreem... Et lineaarsete homogeensete võrrandite süsteemil oleks nullist erinev lahendus, on vajalik ja piisav, et Δ ≠ 0.
  Niisiis, kui determinant Δ ≠ 0, on süsteemil ainulaadne lahendus.
  Kui Δ ≠ 0, siis on lineaarsete homogeensete võrrandite süsteemil lõpmatu hulk lahendusi.
  Teoreem... Selleks, et homogeensel süsteemil oleks nullist erinev lahendus, on see vajalik ja piisav r (A)< n .
  Tõestus:
  1) r rohkem ei saa olla n(maatriksi auaste ei ületa veergude või ridade arvu);
  2) r< n aastast kui r = n, siis on süsteemi peamine determinant Δ ≠ 0 ja Crameri valemite järgi on ainulaadne triviaalne lahendus x 1 = x 2 =… = x n = 0, mis on tingimusega vastuolus. Tähendab, r (A)< n .
  Tagajärg... Selleks, et süsteem oleks homogeenne n lineaarvõrrandid n unknowns on nulliväline lahendus, on vajalik ja piisav, et Δ = 0.

KOOS n tundmatu on vormisüsteem:

kus a ij ja b i (i = 1, ..., m; b = 1, ..., n) on mõned teadaolevad numbrid ja x 1, ..., x n - tundmatud numbrid... Koefitsientide määramisel a ij indeks i määrab võrrandi arvu ja teine j- tundmatute arv, kellel on see koefitsient.

Homogeenne süsteem - kui kõik süsteemi vabad liikmed on võrdsed nulliga ( b 1 = b 2 =… = b m = 0), olukord on vastupidine heterogeenne süsteem.

Ruudukujuline süsteem - kui number m võrrandid on võrdsed arvuga n teadmata.

Süsteemi lahendus- agregaat n numbrid c 1, c 2, ..., c n, selline, et kõik asendatakse c i selle asemel x i süsteemiks muudab kõik selle võrrandid identiteete.

Koostöösüsteem - kui süsteemil on vähemalt üks lahendus ja ebajärjekindel süsteem kui süsteemil pole lahendusi.

Seda tüüpi ühendussüsteemil (nagu eespool kirjeldatud, olgu see (1)) võib olla üks või mitu lahendust.

Lahendused c 1 (1), c 2 (1), ..., c n (1) ja c 1 (2), c 2 (2), ..., c n (2) tüüpi (1) liigendsüsteem erinevaid, kui isegi 1 võrdsus ebaõnnestub:

c 1 (1) = c 1 (2), c 2 (1) = c 2 (2), ..., c n (1) = c n (2).

Ühine süsteem (1) on teatud kui tal on ainult üks lahendus; kui süsteemis on vähemalt 2 erinevaid lahendusi, temast saab alamääratletud... Kui võrrandeid on rohkem kui tundmatuid, on süsteem seda uuesti määratletud.

Tundmatute koefitsiendid kirjutatakse maatriksina:

Seda nimetatakse süsteemi maatriks.

Arvud võrrandite paremal küljel b 1, ..., b m on vabad liikmed.

Täitematerjal n numbrid c 1, ..., c n on lahendus sellele süsteemile, kui kõik süsteemi võrrandid muutuvad pärast numbrite asendamist võrdseks c 1, ..., c n vastavate tundmatute asemel x 1, ..., x n.

Lineaarsete võrrandite süsteemi lahendamisel võib tekkida 3 võimalust:

1. Süsteemil on ainult üks lahendus.

2. Süsteemil on lõputult palju lahendusi. Näiteks,. Selle süsteemi lahenduseks on kõik numbripaarid, mis erinevad märgi poolest.

3. Süsteemil pole lahendusi. Näiteks, kui lahendus oleks olemas, siis x 1 + x 2 oleks võrdne 0 ja 1 korraga.

Lineaarvõrrandisüsteemide lahendamise meetodid.

Otsesed meetodid anna algoritm täpse lahenduse leidmiseks SLAU(lineaarsete algebraliste võrrandite süsteemid). Ja kui täpsus oleks absoluutne, leiaksid nad selle üles. Tõeline elektroarvuti töötab muidugi veaga, seega on lahendus ligikaudne.

Lineaarvõrrandite süsteemid. Loeng 6.

Lineaarvõrrandite süsteemid.

Põhimõisted.

Vaate süsteem

helistas süsteem - lineaarvõrrandid tundmatutega.

Numbreid ,, kutsutakse süsteemi koefitsiendid.

Numbreid kutsutakse vabad süsteemi liikmed, – süsteemi muutujad... Maatriks

helistas süsteemi peamine maatriks ja maatriks

– maatriksi laiendatud süsteem... Maatriksid - veerud

Ja vastavalt vabade liikmete ja süsteemi tundmatute maatriksid... Seejärel saab maatriksvormis vormis võrrandisüsteemi kirjutada. Süsteemi lahendus nimetatakse muutujate väärtusteks, kui need asendatakse, muutuvad kõik süsteemi võrrandid tõelisteks numbrilisteks võrdsusteks. Süsteemi mis tahes lahendust saab esitada maatriksi - veeru kujul. Siis kehtib maatriksi võrdsus.

Võrrandisüsteemi nimetatakse ühine kui sellel on vähemalt üks lahendus ja ebajärjekindel kui sellel pole lahendust.

Lineaarvõrrandite süsteemi lahendamine tähendab selle ühilduvuse väljaselgitamist ja ühilduvuse korral selle üldlahenduse leidmist.

Süsteemi nimetatakse homogeenne kui kõik selle vabad liikmed on võrdsed nulliga. Homogeenne süsteem on alati ühilduv, kuna sellel on lahendus

Kroneckeri - Copelli teoreem.

Vastus küsimusele lineaarsete süsteemide lahenduste olemasolu ja nende ainulaadsuse kohta võimaldab meil saada järgmise tulemuse, mille saab sõnastada järgmiste väidetena tundmatutega lineaarvõrrandite süsteemi kohta

(1)

Teoreem 2... Lineaarvõrrandite süsteem (1) on järjepidev ainult siis ja ainult siis, kui põhimaatriksi auaste on võrdne laiendatud (.

Teoreem 3... Kui lineaarvõrrandite ühissüsteemi põhimaatriksi auaste on võrdne tundmatute arvuga, siis on süsteemil ainulaadne lahendus.

Teoreem 4... Kui liigesüsteemi põhimaatriksi auaste vähem numbrit tundmatuid, siis on süsteemil lõpmatu hulk lahendusi.

Süsteemilahenduse reeglid.

3. Leidke peamiste muutujate väljendus vabade kujul ja hankige süsteemi üldlahendus.

4. Andes vabadele muutujatele suvalisi väärtusi, saadakse kõik peamiste muutujate väärtused.

Lineaarvõrrandisüsteemide lahendamise meetodid.

Pöördmaatriksi meetod.

pealegi on süsteemil ainulaadne lahendus. Kirjutame süsteemi maatriksi kujul

kus , , .

Korrutame maatriksi vasakpoolse maatriksvõrrandi mõlemad küljed maatriksiga

Sellest ajast saame, kust saame võrdsuse tundmatute leidmiseks

Näide 27. Lahendage pöördmaatriksi meetodit kasutades lineaarvõrrandite süsteem

Lahendus. Tähistame süsteemi põhimaatriksiga

.

Laseme, siis leiame lahenduse valemi abil.

Arvutame.

Sellest ajast alates on süsteemil ainulaadne lahendus. Leidke kõik algebralised täiendid

, ,

, ,

, ,

, ,

Seega

.

Kontrollime

.

Pöördmaatriks leiti õigesti. Siit leiame valemi abil muutujate maatriksi.

.

Maatriksite väärtusi võrreldes saame vastuse :.

Crameri meetod.

Olgu antud tundmatutega lineaarvõrrandite süsteem

pealegi on süsteemil ainulaadne lahendus. Kirjutame süsteemi lahendi üles maatriksi kujul või

Me tähistame

. . . . . . . . . . . . . . ,

Seega saame valemid tundmatute väärtuste leidmiseks, mida nimetatakse Crameri valemid.

Näide 28. Lahendage järgmine lineaarvõrrandite süsteem Crameri meetodil .

Lahendus. Leiame süsteemi põhimaatriksi determinandi

.

Sellest ajast alates on süsteemil üks lahendus.

Leiame Crameri valemite ülejäänud määrajad

,

,

.

Crameri valemite abil leiame muutujate väärtused

Gaussi meetod.

Meetod seisneb muutujate järjestikuses kõrvaldamises.

Olgu antud tundmatutega lineaarvõrrandite süsteem.

Gaussi lahendusprotsess koosneb kahest etapist:

Esimeses etapis vähendatakse süsteemi laiendatud maatriksit, kasutades elementaarseid teisendusi astmeliseks

,

kus, millele süsteem vastab

Pärast seda muutujad loetakse vabaks ja kantakse igas võrrandis paremale küljele.

Teises etapis väljendatakse muutuja viimasest võrrandist, saadud väärtus asendatakse võrrandiga. Sellest võrrandist

muutuja on väljendatud. See protsess jätkub kuni esimese võrrandini. Tulemuseks on peamiste muutujate väljendus vabade muutujate osas .

Näide 29. Lahendage järgmine süsteem Gaussi meetodil

Lahendus. Kirjutame süsteemi laiendatud maatriksi välja ja vähendame selle astmeliseks

.

Sest rohkem kui tundmatute arv, siis on süsteem järjepidev ja sellel on lõpmatu hulk lahendusi. Kirjutame astmelise maatriksi süsteemi

Selle süsteemi kolmest esimesest veerust koosneva laiendatud maatriksi determinant ei ole võrdne nulliga, seega peetakse seda põhiliseks. Muutujad

Need on põhilised ja muutuja on tasuta. Me kanname selle kõikides võrrandites vasakule küljele

Viimasest võrrandist, mida me väljendame

Asendades selle väärtuse eelviimases teises võrrandis, saame

kus ... Asendades muutujate väärtused esimesse võrrandisse, leiame ... Vastuse kirjutame järgmisel kujul

Teie privaatsus on meile oluline. Sel põhjusel oleme välja töötanud privaatsuspoliitika, mis kirjeldab, kuidas me teie teavet kasutame ja salvestame. Palun lugege meie privaatsuspoliitikat ja andke meile teada, kui teil on küsimusi.

Isikuandmete kogumine ja kasutamine

Isikuandmed viitavad andmetele, mida saab kasutada konkreetse isiku tuvastamiseks või temaga ühenduse võtmiseks.

Kui te meiega ühendust võtate, võidakse teil igal ajal paluda esitada oma isiklikud andmed.

Allpool on mõned näited isikuandmete tüüpidest, mida me võime koguda ja kuidas me võime seda teavet kasutada.

Milliseid isikuandmeid me kogume:

• Kui jätate saidile päringu, võime koguda mitmesugust teavet, sealhulgas teie nime, telefoninumbrit, e -posti aadressi jne.

Kuidas me teie isikuandmeid kasutame:

• Kogutud isikuandmed võimaldavad meil teiega ühendust võtta ja teatada ainulaadsetest pakkumistest, tutvustustest ja muudest sündmustest ning eelseisvatest sündmustest.
• Aeg -ajalt võime kasutada teie isikuandmeid oluliste märguannete ja sõnumite saatmiseks.
• Võime kasutada isikuandmeid ka sisemistel eesmärkidel, näiteks auditite tegemiseks, andmete analüüsimiseks ja erinevateks uuringuteks, et parandada meie pakutavaid teenuseid ja anda teile soovitusi meie teenuste kohta.
• Kui osalete auhinnaloosis, konkursil või sarnasel reklaamüritusel, võime kasutada teie edastatud teavet selliste programmide haldamiseks.

Teabe avalikustamine kolmandatele isikutele

Me ei avalda teilt saadud teavet kolmandatele osapooltele.

Erandid:

• Kui on vaja - vastavalt seadusele, kohtumäärusele, kohtumenetluses ja / või Vene Föderatsiooni territooriumil asuvate valitsusasutuste avalike päringute või taotluste alusel - avaldada teie isikuandmeid. Samuti võime teie kohta teavet avaldada, kui leiame, et selline avalikustamine on vajalik või asjakohane turvalisuse, õiguskaitse või muude sotsiaalselt oluliste põhjuste tõttu.
• Ümberkorraldamise, ühinemise või müügi korral võime edastada kogutud isikuandmed asjakohasele kolmandale isikule - õigusjärglasele.

Isikuandmete kaitse

Võtame ettevaatusabinõusid - sealhulgas administratiivseid, tehnilisi ja füüsilisi -, et kaitsta teie isikuandmeid kadumise, varguse ja väärkohtlemise eest, samuti volitamata juurdepääsu, avalikustamise, muutmise ja hävitamise eest.

Austa oma privaatsust ettevõtte tasandil

Teie isikuandmete turvalisuse tagamiseks tutvustame oma töötajatele konfidentsiaalsuse ja turvalisuse reegleid ning jälgime rangelt konfidentsiaalsusmeetmete rakendamist.