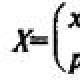Импульс тела

Импульсом тела называется величина, равная произведению массы тела на его скорость.

Следует помнить, что речь идет о теле, которое можно представить как материальную точку. Импульс тела ($р$) называют также количеством движения. Понятие количества движения было введено в физику Рене Декартом (1596—1650). Термин «импульс» появился позже (impulsus в переводе с латинского означает «толчок»). Импульс является векторной величиной (как и скорость) и выражается формулой:

$p↖{→}=mυ↖{→}$

Направление вектора импульса всегда совпадает с направлением скорости.

За единицу импульса в СИ принимают импульс тела массой $1$ кг, движущегося со скоростью $1$ м/с, следовательно, единицей импульса является $1$ кг $·$ м/с.

Если на тело (материальную точку) действует постоянная сила в течение промежутка времени $∆t$, то постоянным будет и ускорение:

$a↖{→}={{υ_2}↖{→}-{υ_1}↖{→}}/{∆t}$

где, ${υ_1}↖{→}$ и ${υ_2}↖{→}$ — начальная и конечная скорости тела. Подставив это значение в выражение второго закона Ньютона, получим:

${m({υ_2}↖{→}-{υ_1}↖{→})}/{∆t}=F↖{→}$

Раскрыв скобки и воспользовавшись выражением для импульса тела, имеем:

${p_2}↖{→}-{p_1}↖{→}=F↖{→}∆t$

Здесь ${p_2}↖{→}-{p_1}↖{→}=∆p↖{→}$ — изменение импульса за время $∆t$. Тогда предыдущее уравнение примет вид:

$∆p↖{→}=F↖{→}∆t$

Выражение $∆p↖{→}=F↖{→}∆t$ представляет собой математическую запись второго закона Ньютона.

Произведение силы на время ее действия называют импульсом силы . Поэтому изменение импульса точки равно изменению импульса силы, действующей на нее.

Выражение $∆p↖{→}=F↖{→}∆t$ называется уравнением движения тела . Следует заметить, что одно и то же действие — изменение импульса точки — может быть получено малой силой за большой промежуток времени и большой силой за малый промежуток времени.

Импульс системы тел. Закон изменения импульса

Импульсом (количеством движения) механической системы называется вектор, равный сумме импульсов всех материальных точек этой системы:

${p_{сист}}↖{→}={p_1}↖{→}+{p_2}↖{→}+...$

Законы изменения и сохранения импульса являются следствием второго и третьего законов Ньютона.

Рассмотрим систему, состоящую из двух тел. Силы ($F_{12}$ и $F_{21}$ на рисунке, с которыми тела системы взаимодействуют между собой, называются внутренними.

Пусть кроме внутренних сил на систему действуют внешние силы ${F_1}↖{→}$ и ${F_2}↖{→}$. Для каждого тела можно записать уравнение $∆p↖{→}=F↖{→}∆t$. Сложив левые и правые части этих уравнений, получим:

${∆p_1}↖{→}+{∆p_2}↖{→}=({F_{12}}↖{→}+{F_{21}}↖{→}+{F_1}↖{→}+{F_2}↖{→})∆t$

Согласно третьему закону Ньютона ${F_{12}}↖{→}=-{F_{21}}↖{→}$.

Следовательно,

${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$

В левой части стоит геометрическая сумма изменений импульсов всех тел системы, равная изменению импульса самой системы — ${∆p_{сист}}↖{→}$.С учетом этого равенство ${∆p_1}↖{→}+{∆p_2}↖{→}=({F_1}↖{→}+{F_2}↖{→})∆t$ можно записать:

${∆p_{сист}}↖{→}=F↖{→}∆t$

где $F↖{→}$ — сумма всех внешних сил, действующих на тело. Полученный результат означает, что импульс системы могут изменить только внешние силы, причем изменение импульса системы направлено так же, как суммарная внешняя сила. В этом суть закона изменения импульса механической системы.

Внутренние силы изменить суммарный импульс системы не могут. Они лишь меняют импульсы отдельных тел системы.

Закон сохранения импульса

Из уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ вытекает закон сохранения импульса. Если на систему не действуют никакие внешние силы, то правая часть уравнения ${∆p_{сист}}↖{→}=F↖{→}∆t$ обращается в ноль, что означает неизменность суммарного импульса системы:

${∆p_{сист}}↖{→}=m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=const$

Система, на которую не действуют никакие внешние силы или равнодействующая внешних сил равна нулю, называется замкнутой.

Закон сохранения импульса гласит:

Суммарный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел системы между собой.

Полученный результат справедлив для системы, содержащей произвольное число тел. Если сумма внешних сил не равна нулю, но сумма их проекций на какое-то направление равна нулю, то проекция импульса системы на это направление не меняется. Так, например, система тел на поверхности Земли не может считаться замкнутой из-за силы тяжести, действующей на все тела, однако сумма проекций импульсов на горизонтальное направление может оставаться неизменной (при отсутствии трения), т. к. в этом направлении сила тяжести не действует.

Реактивное движение

Рассмотрим примеры, подтверждающие справедливость закона сохранения импульса.

Возьмем детский резиновый шарик, надуем его и отпустим. Мы увидим, что когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Движение шарика является примером реактивного движения. Объясняется оно законом сохранения импульса: суммарный импульс системы «шарик плюс воздух в нем» до истечения воздуха равен нулю; он должен остаться равным нулю и во время движения; поэтому шарик движется в сторону, противоположную направлению истечения струи, и с такой скоростью, что его импульс по модулю равен импульсу воздушной струи.

Реактивным движением называют движение тела, возникающее при отделении от него с какой- либо скоростью некоторой его части. Вследствие закона сохранения импульса направление движения тела при этом противоположно направлению движения отделившейся части.

На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат. Масса ракеты складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной, или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.

Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Согласно закону сохранения импульса, импульс $m_{p}υ_p$, приобретаемый ракетой, должен быть равен импульсу $m_{газ}·υ_{газ}$ выброшенных газов:

$m_{p}υ_p=m_{газ}·υ_{газ}$

Отсюда следует, что скорость ракеты

$υ_p=({m_{газ}}/{m_p})·υ_{газ}$

Из этой формулы видно, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.

Формула $υ_p=({m_{газ}}/{m_p})·υ_{газ}$ является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты была получена в 1897 г. К. Э. Циолковским и носит его имя.

Работа силы

Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.

Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:

$A=F|∆r↖{→}|cosα$

где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.

Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.

Работа — величина скалярная. Если $α 0$, а если $90°

При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.

Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.

Работа силы тяжести

Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.

Выразим $∆x$ через $H$ и $α$:

$∆x={H}/{sinα}$

Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° - α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:

$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$

Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.

Отсюда следует, что:

1. работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
2. при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).

Работа сил реакции , равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.

Работа силы трения

Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:

$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$

Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то

$A_{тр}=μmgHctgα$

Работа силы упругости

Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.

Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:

$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$

Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:

$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$

Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.

Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.

Мощность силы

Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.

Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).

Мощность определяется формулой:

где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.

Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:

$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$

Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.

Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.

Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.

В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.

Кинетическая энергия. Закон изменения кинетической энергии

Если тело или несколько взаимодействующих между собой тел (система тел) могут совершать работу, то говорят, что они обладают энергией.

Слово «энергия» (от греч. energia — действие, деятельность) нередко употребляется в быту. Так, например, людей, которые могут быстро выполнять работу, называют энергичными, обладающими большой энергией.

Энергия, которой обладает тело вследствие движения, называется кинетической энергией.

Как и в случае определения энергии вообще, о кинетической энергии можно сказать, что кинетическая энергия — это способность движущегося тела совершать работу.

Найдем кинетическую энергию тела массой $m$, движущегося со скоростью $υ$. Поскольку кинетическая энергия — это энергия, обусловленная движением, нулевым состоянием для нее является то состояние, в котором тело покоится. Найдя работу, необходимую для сообщения телу данной скорости, мы найдем его кинетическую энергию.

Для этого подсчитаем работу на участке перемещения $∆r↖{→}$ при совпадении направлений векторов силы $F↖{→}$ и перемещения $∆r↖{→}$. В этом случае работа равна

где $∆x=∆r$

Для движения точки с ускорением $α=const$ выражение для перемещения имеет вид:

$∆x=υ_1t+{at^2}/{2},$

где $υ_1$ — начальная скорость.

Подставив в уравнение $A=F·∆x$ выражение для $∆x$ из $∆x=υ_1t+{at^2}/{2}$ и воспользовавшись вторым законом Ньютона $F=ma$, получим:

$A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$

Выразив ускорение через начальную $υ_1$ и конечную $υ_2$ скорости $a={υ_2-υ_1}/{t}$ и подставив в $A=ma(υ_1t+{at^2}/{2})={mat}/{2}(2υ_1+at)$ имеем:

$A={m(υ_2-υ_1)}/{2}·(2υ_1+υ_2-υ_1)$

$A={mυ_2^2}/{2}-{mυ_1^2}/{2}$

Приравняв теперь начальную скорость к нулю: $υ_1=0$, получим выражение для кинетической энергии:

$E_K={mυ}/{2}={p^2}/{2m}$

Таким образом, движущееся тело обладает кинетической энергией. Эта энергия равна работе, которую необходимо совершить, чтобы увеличить скорость тела от нуля до значения $υ$.

Из $E_K={mυ}/{2}={p^2}/{2m}$ следует, что работа силы по перемещению тела из одного положения в другое равна изменению кинетической энергии:

$A=E_{K_2}-E_{K_1}=∆E_K$

Равенство $A=E_{K_2}-E_{K_1}=∆E_K$ выражает теорему об изменении кинетической энергии.

Изменение кинетической энергии тела (материальной точки) за некоторый промежуток времени равно работе, совершенной за это время силой, действующей на тело.

Потенциальная энергия

Потенциальной энергией называется энергия, определяемая взаимным расположением взаимодействующих тел или частей одного и того же тела.

Поскольку энергия определяется как способность тела совершать работу, то потенциальную энергию, естественно, определяют как работу силы, зависящую только от взаимного расположения тел. Таковой является работа силы тяжести $A=mgh_1-mgh_2=mgH$ и работа силы упругости:

$A={kx_0^2}/{2}-{kx^2}/{2}$

Потенциальной энергией тела, взаимодействующего с Землей, называют величину, равную произведению массы $m$ этого тела на ускорение свободного падения $g$ и на высоту $h$ тела над поверхностью Земли:

Потенциальной энергией упруго деформированного тела называют величину, равную половине произведения коэффициента упругости (жесткости) $k$ тела на квадрат деформации $∆l$:

$E_p={1}/{2}k∆l^2$

Работа консервативных сил (тяжести и упругости) с учетом $E_p=mgh$ и $E_p={1}/{2}k∆l^2$ выражается следующим образом:

$A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$

Эта формула позволяет дать общее определение потенциальной энергии.

Потенциальной энергией системы называется зависящая от положения тел величина, изменение которой при переходе системы из начального состояния в конечное равно работе внутренних консервативных сил системы, взятой с противоположным знаком.

Знак «минус» в правой части уравнения $A=E_{p_1}-E_{p_2}=-(E_{p_2}-E_{p_1})=-∆E_p$ означает, что при совершении работы внутренними силами (например, падение тела на землю под действием силы тяжести в системе «камень — Земля») энергия системы убывает. Работа и изменение потенциальной энергии в системе всегда имеют противоположные знаки.

Поскольку работа определяет лишь изменение потенциальной энергии, то физический смысл в механике имеет только изменение энергии. Поэтому выбор нулевого уровня энергии произволен и определяется исключительно соображениями удобства, например, простотой записи соответствующих уравнений.

Закон изменения и сохранения механической энергии

Полной механической энергией системы называется сумма ее кинетической и потенциальной энергий:

Она определяется положением тел (потенциальная энергия) и их скоростью (кинетическая энергия).

Согласно теореме о кинетической энергии,

$E_k-E_{k_1}=A_p+A_{пр},$

где $А_р$ — работа потенциальных сил, $А_{пр}$ — работа непотенциальных сил.

В свою очередь, работа потенциальных сил равна разности потенциальной энергии тела в начальном $Е_{р_1}$ и конечном $Е_р$ состояниях. Учитывая это, получим выражение для закона изменения механической энергии:

$(E_k+E_p)-(E_{k_1}+E_{p_1})=A_{пр}$

где левая часть равенства — изменение полной механической энергии, а правая — работа непотенциальных сил.

Итак, закон изменения механической энергии гласит:

Изменение механической энергии системы равно работе всех непотенциальных сил.

Механическая система, в которой действуют только потенциальные силы, называется консервативной.

В консервативной системе $А_{пр} = 0$. Отсюда следует закон сохранения механической энергии:

В замкнутой консервативной системе полная механическая энергия сохраняется (не изменяется со временем):

$E_k+E_p=E_{k_1}+E_{p_1}$

Закон сохранения механической энергии выводится из законов механики Ньютона, которые применимы для системы материальных точек (или макрочастиц).

Однако закон сохранения механической энергии справедлив и для системы микрочастиц, где сами законы Ньютона уже не действуют.

Закон сохранения механической энергии является следствием однородности времени.

Однородность времени состоит в том, что при одинаковых начальных условиях протекание физических процессов не зависит от того, в какой момент времени эти условия созданы.

Закон сохранения полной механической энергии означает, что при изменении кинетической энергии в консервативной системе должна меняться и ее потенциальная энергия, так что их сумма остается постоянной. Это означает возможность превращения одного вида энергии в другой.

В соответствии с различными формами движения материи рассматривают различные виды энергии: механическую, внутреннюю (равную сумме кинетической энергии хаотического движения молекул относительно центра масс тела и потенциальной энергии взаимодействия молекул друг с другом), электромагнитную, химическую (которая складывается из кинетической энергии движения электронов и электрической энергии их взаимодействия друг с другом и с атомными ядрами), ядерную и пр. Из сказанного видно, что деление энергии на разные виды достаточно условно.

Явления природы обычно сопровождаются превращением одного вида энергии в другой. Так, например, трение частей различных механизмов приводит к превращению механической энергии в тепло, т. е. во внутреннюю энергию. В тепловых двигателях, наоборот, происходит превращение внутренней энергии в механическую; в гальванических элементах химическая энергия превращается в электрическую и т. д.

В настоящее время понятие энергии является одним из основных понятий физики. Это понятие неразрывно связано с представлением о превращении одной формы движения в другую.

Вот как в современной физике формулируется понятие энергии:

Энергия — общая количественная мера движения и взаимодействия всех видов материи. Энергия не возникает из ничего и не исчезает, она может только переходить из одной формы в другую. Понятие энергии связывает воедино все явления природы.

Простые механизмы. КПД механизмов

Простыми механизмами называются приспособления, изменяющие величину или направление приложенных к телу сил.

Они применяются для перемещения или подъема больших грузов с помощью небольших усилий. К ним относятся рычаг и его разновидности — блоки (подвижный и неподвижный), ворот, наклонная плоскость и ее разновидности — клин, винт и др.

Рычаг. Правило рычага

Рычаг представляет собой твердое тело, способное вращаться вокруг неподвижной опоры.

Правило рычага гласит:

Рычаг находится в равновесии, если приложенные к нему силы обратно пропорциональны их плечам:

${F_2}/{F_1}={l_1}/{l_2}$

Из формулы ${F_2}/{F_1}={l_1}/{l_2}$, применив к ней свойство пропорции (произведение крайних членов пропорции равно произведению ее средних членов), можно получить такую формулу:

Но $F_1l_1=M_1$ — момент силы, стремящейся повернуть рычаг по часовой стрелке, а $F_2l_2=M_2$ — момент силы, стремящейся повернуть рычаг против часовой стрелки. Таким образом, $M_1=M_2$, что и требовалось доказать.

Рычаг начал применяться людьми в глубокой древности. С его помощью удавалось поднимать тяжелые каменные плиты при постройке пирамид в Древнем Египте. Без рычага это было бы невозможно. Ведь, например, для возведения пирамиды Хеопса, имеющей высоту $147$ м, было использовано более двух миллионов каменных глыб, самая меньшая из которых имела массу $2.5$ тонн!

В наше время рычаги находят широкое применение как на производстве (например, подъемные краны), так и в быту (ножницы, кусачки, весы).

Неподвижный блок

Действие неподвижного блока аналогично действию рычага с равными плечами: $l_1=l_2=r$. Приложенная сила $F_1$ равна нагрузке $F_2$, и условие равновесия имеет вид:

Неподвижный блок применяют, когда нужно изменить направление силы, не меняя ее величину.

Подвижный блок

Подвижный блок действует аналогично рычагу, плечи которого составляют: $l_2={l_1}/{2}=r$. При этом условие равновесия имеет вид:

где $F_1$ — приложенная сила, $F_2$ — нагрузка. Применение подвижного блока дает выигрыш в силе в два раза.

Полиспаст (система блоков)

Обычный полиспаст состоит из $n$ подвижных и $n$ неподвижных блоков. Его применив дает выигрыш в силе в $2n$ раз:

$F_1={F_2}/{2n}$

Степенной полиспаст состоит из п подвижных и одного неподвижного блока. Применение степенного полиспаста дает выигрыш в силе в $2^n$ раз:

$F_1={F_2}/{2^n}$

Винт

Винт представляет собой наклонную плоскость, навитую на ось.

Условие равновесия сил, действующих на винт, имеет вид:

$F_1={F_2h}/{2πr}=F_2tgα, F_1={F_2h}/{2πR}$

где $F_1$ — внешняя сила, приложенная к винту и действующая на расстоянии $R$ от его оси; $F_2$ — сила, действующая в направлении оси винта; $h$ — шаг винта; $r$ — средний радиус резьбы; $α$ — угол наклона резьбы. $R$ — длина рычага (гаечного ключа), вращающего винт с силой $F_1$.

Коэффициент полезного действия

Коэффициент полезного действия (КПД) — отношение полезной работы ко всей затраченной работе.

Коэффициент полезного действия часто выражают в процентах и обозначают греческой буквой $η$ («эта»):

$η={A_п}/{A_3}·100%$

где $А_п$ — полезная работа, $А_3$ — вся затраченная работа.

Полезная работа всегда составляет лишь часть полной работы, которую затрачивает человек, используя тот или иной механизм.

Часть совершенной работы тратится на преодоление сил трения. Поскольку $А_3 > А_п$, КПД всегда меньше $1$ (или $< 100%$).

Поскольку каждую из работ в этом равенстве можно выразить в виде произведения соответствующей силы на пройденный путь, то его можно переписать так: $F_1s_1≈F_2s_2$.

Отсюда следует, что, выигрывая с помощью механизма в силе, мы во столько же раз проигрываем в пути, и наоборот . Этот закон называют золотым правилом механики.

Золотое правило механики является приближенным законом, так как в нем не учитывается работа по преодолению трения и силы тяжести частей используемых приспособлений. Тем не менее оно бывает очень полезным при анализе работы любого простого механизма.

Так, например, благодаря этому правилу сразу можно сказать, что рабочему, изображенному на рисунке, при двукратном выигрыше в силе подъема груза на $10$ см придется опустить противоположный конец рычага на $20$ см.

Столкновение тел. Упругий и неупругий удары

Законы сохранения импульса и механической энергии применяются для решения задачи о движении тел после столкновения: по известным импульсам и энергиям до столкновения определяются значения этих величин после столкновения. Рассмотрим случаи упругого и неупругого ударов.

Абсолютно неупругим называется удар, после которого тела образуют единое тело, движущееся с определенной скоростью. Задача о скорости последнего решается с помощью закона сохранения импульса системы тел с массами $m_1$ и $m_2$ (если речь идет о двух телах) до и после удара:

$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=(m_1+m_2)υ↖{→}$

Очевидно, что кинетическая энергия тел при неупругом ударе не сохраняется (например, при ${υ_1}↖{→}=-{υ_2}↖{→}$ и $m_1=m_2$ она становится равной нулю после удара).

Абсолютно упругим называется удар, при котором сохраняется не только сумма импульсов, но и сумма кинетических энергий ударяющихся тел.

Для абсолютно упругого удара справедливы уравнения

$m_1{υ_1}↖{→}+m_2{υ_2}↖{→}=m_1{υ"_1}↖{→}+m_2{υ"_2}↖{→};$

${m_{1}υ_1^2}/{2}+{m_{2}υ_2^2}/{2}={m_1(υ"_1)^2}/{2}+{m_2(υ"_2)^2}/{2}$

где $m_1, m_2$ — массы шаров, $υ_1, υ_2$ —скорости шаров до удара, $υ"_1, υ"_2$ —скорости шаров после удара.

3.2. Импульс

3.2.2. Изменение импульса тела

Для применения законов изменения и сохранения импульса необходимо уметь рассчитывать изменение импульса.

Изменение импульса Δ P → тела определяется формулой

Δ P → = P → 2 − P → 1 ,

где P → 1 = m v → 1 - начальный импульс тела; P → 2 = m v → 2 - его конечный импульс; m - масса тела; v → 1 - начальная скорость тела; v → 2 - его конечная скорость.

Для вычисления изменения импульса тела целесообразно применять следующий алгоритм :

1) выбрать систему координат и найти проекции начального P → 1 и конечного P → 2 импульсов тела на координатные оси:

P 1 x , P 2 x ;

P 1 y , P 2 y ;

∆P x = P 2 x − P 1 x ;

∆P y = P 2 y − P 1 y ;

3) вычислить модуль вектора изменения импульса Δ P → как

Δ P = Δ P x 2 + Δ P y 2 .

Пример 4. Тело падает под углом 30° к вертикали на горизонтальную плоскость. Определить модуль изменения импульса тела за время удара, если к моменту соприкосновения с плоскостью модуль импульса тела равен 15 кг · м/с. Удар тела о плоскость считать абсолютно упругим.

Решение. Тело, падающее на горизонтальную поверхность под некоторым углом α к вертикали и соударяющееся с данной поверхностью абсолютно упруго,

• во-первых, сохраняет неизменным модуль своей скорости, а значит, и величину импульса:

P 1 = P 2 = P ;

• во-вторых, отражается от поверхности под тем же углом, под каким падает на нее:

α 1 = α 2 = α,

где P 1 = mv 1 - модуль импульса тела до удара; P 2 = mv 2 - модуль импульса тела после удара; m - масса тела; v 1 - величина скорости тела до удара; v 2 - величина скорости тела после удара; α 1 - угол падения; α 2 - угол отражения.

Указанные импульсы тела, углы и система координат показаны на рисунке.

Для расчета модуля изменения импульса тела воспользуемся алгоритмом :

1) запишем проекции импульсов до удара и после удара тела о поверхность на координатные оси:

P 1 x = mv  sin α, P 2 x = mv  sin α;

P 1 y = −mv  cos α, P 2 y = mv  cos α;

2) найдем проекции изменения импульса на координатные оси по фор­мулам

Δ P x = P 2 x − P 1 x = m v sin α − m v sin α = 0 ;

Δ P y = P 2 y − P 1 y = m v cos α − (− m v cos α) = 2 m v cos α ;

Δ P = (Δ P x) 2 + (Δ P y) 2 = (Δ P y) 2 = | Δ P y | = 2 m v cos α .

Величина P = mv задана в условии задачи; следовательно, вычисление модуля изменения импульса произведем по формуле

Δ P = 2 P cos 30 ° = 2 ⋅ 15 ⋅ 0,5 3 ≈ 26 кг ⋅ м/с.

Пример 5. Камень массой 50 г брошен под углом 45° к горизонту со скоростью 20 м/с. Найти модуль изменения импульса камня за время полета. Сопротивлением воздуха пренебречь.

Решение. Если сопротивление воздуха отсутствует, то тело движется по симметричной параболе; при этом

• во-первых, вектор скорости в точке падения тела составляет с горизонтом угол β, равный углу α (α - угол между вектором скорости тела в точке бросания и горизонтом):

• во-вторых, модули скоростей в точке бросания v 0 и в точке падения тела v также одинаковы:

v 0 = v ,

где v 0 - величина скорости тела в точке бросания; v - величина скорости тела в точке падения; α - угол, который составляет вектор скорости с горизонтом в точке бросания тела; β - угол, который составляет с горизонтом вектор скорости в точке падения тела.

Векторы скорости тела (векторы импульса) и углы показаны на рисунке.

Для расчета модуля изменения импульса тела во время полета воспользуемся алгоритмом :

1) запишем проекции импульсов для точки бросания и для точки падения на координатные оси:

P 1 x = mv 0  cos α, P 2 x = mv 0  cos α;

P 1 y = mv 0  sin α, P 2 y = −mv 0  sin α;

2) найдем проекции изменения импульса на координатные оси по формулам

Δ P x = P 2 x − P 1 x = m v 0 cos α − m v 0 cos α = 0 ;

Δ P y = P 2 y − P 1 y = − m v 0 sin α − m v 0 sin α = − 2 m v 0 sin α ;

3) вычислим модуль изменения импульса как

Δ P = (Δ P x) 2 + (Δ P y) 2 = (Δ P y) 2 = | Δ P y | = 2 m v 0 sin α ,

где m - масса тела; v 0 - модуль начальной скорости тела.

Следовательно, вычисление модуля изменения импульса произведем по формуле

Δ P = 2 m v 0 sin 45 ° = 2 ⋅ 50 ⋅ 10 − 3 ⋅ 20 ⋅ 0,5 2 ≈ 1,4 кг ⋅ м/с.

Законы Ньютона позволяют решать различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано, например, с нахождением ускорения движущегося тела, если известны все действующие на это тело силы. А затем по ускорению определяют и другие величины (мгновенную скорость, перемещение и др.).

Но часто бывает очень сложно определить действующие на тело силы. Поэтому для решения многих задач используют ещё одну важнейшую физическую величину - импульс тела.

• Импульсом тела р называется векторная физическая величина, равная произведению массы тела на его скорость

Импульс - векторная величина. Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

За единицу импульса в СИ принимают импульс тела массой 1 кг, движущегося со скоростью 1 м/с. Значит, единицей импульса тела в СИ является 1 кг м/с.

При расчётах пользуются уравнением для проекций векторов: р х = mv x .

В зависимости от направления вектора скорости по отношению к выбранной оси X проекция вектора импульса может быть как положительной, так и отрицательной.

Слово «импульс» (impulsus) в переводе с латинского означает «толчок». В некоторых книгах вместо термина «импульс» используется термин «количество движения».

Эта величина была введена в науку примерно в тот же период времени, когда Ньютоном были открыты законы, названные впоследствии его именем (т. е. в конце XVII в.).

При взаимодействии тел их импульсы могут изменяться. В этом можно убедиться на простом опыте.

Два шарика одинаковой массы подвешивают на нитяных петлях к укреплённой на кольце штатива деревянной линейке, как показано на рисунке 44, а.

Рис. 44. Демонстрация закона сохранения импульса

Шарик 2 отклоняют от вертикали на угол а (рис. 44, б) и отпускают. Вернувшись в прежнее положение, он ударяет по шарику 1 и останавливается. При этом шарик 1 приходит в движение и отклоняется на тот же угол а (рис. 44, в).

В данном случае очевидно, что в результате взаимодействия шаров импульс каждого из них изменился: на сколько уменьшился импульс шара 2, на столько же увеличился импульс шара 1.

Если два или несколько тел взаимодействуют только между собой (т. е. не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.

Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом. Но

• векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел

В этом заключается закон сохранения импульса.

Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю. Покажем это, воспользовавшись для вывода закона сохранения импульса вторым и третьим законами Ньютона. Для простоты рассмотрим систему, состоящую только из двух тел - шаров массами m 1 и m 2 , которые движутся прямолинейно навстречу друг другу со скоростями v 1 и v 2 (рис. 45).

Рис. 45. Система из двух тел - шаров, движущихся прямолинейно навстречу друг другу

Силы тяжести, действующие на каждый из шаров, уравновешиваются силами упругости поверхности, по которой они катятся. Значит, действие этих сил можно не учитывать. Силы сопротивления движению в данном случае малы, поэтому их влияние мы тоже не будем учитывать. Таким образом, можно считать, что шары взаимодействуют только друг с другом.

Из рисунка 45 видно, что через некоторое время шары столкнутся. Во время столкновения, длящегося в течение очень короткого промежутка времени t, возникнут силы взаимодействия F 1 и F 2 , приложенные соответственно к первому и второму шару. В результате действия сил скорости шаров изменятся. Обозначим скорости шаров после соударения буквами v 1 и v 2 .

В соответствии с третьим законом Ньютона силы взаимодействия шаров равны по модулю и направлены в противоположные стороны:

По второму закону Ньютона каждую из этих сил можно заменить произведением массы и ускорения, полученного каждым из шаров при взаимодействии:

m 1 а 1 = -m 2 а 2 .

Ускорения, как вы знаете, определяются из равенств:

Заменив в уравнении для сил ускорения соответствующими выражениями, получим:

В результате сокращения обеих частей равенства на t получим:

m1(v" 1 - v 1) = -m 2 (v" 2 - v 2).

Сгруппируем члены этого уравнения следующим образом:

m 1 v 1 " + m 2 v 2 " = m 1 v 1 = m 2 v 2 . (1)

Учитывая, что mv = p, запишем уравнение (1) в таком виде:

P" 1 + Р" 2 = P 1 + Р 2 .(2)

Левые части уравнений (1) и (2) представляют собой суммарный импульс шаров после их взаимодействия, а правые - суммарный импульс до взаимодействия.

Значит, несмотря на то, что импульс каждого из шаров при взаимодействии изменился, векторная сумма их импульсов после взаимодействия осталась такой же, как и до взаимодействия.

Уравнения (1) и (2) являются математической записью закона сохранения импульса.

Поскольку в данном курсе рассматриваются только взаимодействия тел, движущихся вдоль одной прямой, то для записи закона сохранения импульса в скалярной форме достаточно одного уравнения, в которое входят проекции векторных величин на ось X:

m 1 v" 1x + m 2 v" 2х = m 1 v 1x + m 2 v 2x .

Вопросы

1. Что называют импульсом тела?
2. Что можно сказать о направлениях векторов импульса и скорости движущегося тела?
3. Расскажите о ходе опыта, изображённого на рисунке 44. О чём он свидетельствует?
4. Что означает утверждение о том, что несколько тел образуют замкнутую систему?
5. Сформулируйте закон сохранения импульса.
6. Для замкнутой системы, состоящей из двух тел, запишите закон сохранения импульса в виде уравнения, в которое входили бы массы и скорости этих тел. Поясните, что означает каждый символ в этом уравнении.

Упражнение 20

1. Две игрушечные заводные машины, массой по 0,2 кг каждая, движутся прямолинейно навстречу друг другу. Скорость каждой машины относительно земли равна 0,1 м/с. Равны ли векторы импульсов машин; модули векторов импульсов? Определите проекцию импульса каждой из машин на ось X, параллельную их траектории.
2. На сколько изменится (по модулю) импульс автомобиля массой 1 т при изменении его скорости от 54 до 72 км/ч?
3. Человек сидит в лодке, покоящейся на поверхности озера. В какой-то момент он встаёт и идёт с кормы на нос. Что произойдёт при этом с лодкой? Объясните явление на основе закона сохранения импульса.
4. Железнодорожный вагон массой 35 т подъезжает к стоящему на том же пути неподвижному вагону массой 28 т и автоматически сцепляется с ним. После сцепки вагоны движутся прямолинейно со скоростью 0,5 м/с. Какова была скорость вагона массой 35 т перед сцепкой?

Часто в физике говорят об импульсе тела, подразумевая при этом количество движения. На самом же деле это понятие тесно связано с совершенно другой величиной - с силой. Импульс силы - что это, как он вводится в физику, и каков его смысл: все эти вопросы подробно освещены в статье.

Количество движения

Импульс тела и импульс силы - это две взаимосвязанных величины, более того, они практически означают одно и то же. Сначала разберем понятие количества движения.

Количество движения как физическая величина впервые появилось в научных трудах ученых нового времени, в частности в XVII веке. Здесь важно отметить две фигуры: это Галилео Галилей, знаменитый итальянец, который обсуждаемую величину так и называл impeto (импульс), и Исаак Ньютон, великий англичанин, который помимо величины motus (движения) также использовал понятие vis motrix (движущая сила).

Итак, названные ученые под количеством движения понимали произведение массы объекта на скорость его линейного перемещения в пространстве. Это определение на языке математики записывается так:

Обратим внимание, что речь идет о величине векторной (p¯), направленной в сторону движения тела, которая пропорциональна модулю скорости, а роль коэффициента пропорциональности играет масса тела.

Связь импульса силы и изменения величины p¯

Как было сказано выше, помимо количества движения Ньютон ввел еще понятие движущей силы. Эту величину он определил так:

Это всем знакомый закон появления ускорения a¯ у тела в результате воздействия на него некоторой внешней силы F¯. Эта важная формула позволяет вывести закон импульса силы. Заметим, что a¯ - это производная по времени скорости (быстрота изменения v¯), что означает следующее:

F¯ = m*dv¯/dt или F¯*dt = m*dv¯ =>

F¯*dt = dp¯, где dp¯ = m*dv¯

Первая формула во второй строке - это импульс силы, то есть величина, равная произведению силы на промежуток времени, в течение которого она действует на тело. Она измеряется в ньютонах на секунду.

Анализ формулы

Выражение для импульса силы в предыдущем пункте также раскрывает физический смысл этой величины: она показывает, на сколько изменяется количество движения за промежуток времени dt. Заметим, что это изменение (dp¯) совершенно не зависит от общего значения количества движения тела. Импульс силы - это причина изменения количества движения, которая может приводить как к увеличению последнего (когда угол между силой F¯ и скоростью v¯ меньше 90 o), так и к его уменьшению (угол между F¯ и v¯ больше 90 o).

Из анализа формулы следует важный вывод: единицы измерения импульса силы совпадают с таковыми для p¯ (ньютон в секунду и килограмм на метр в секунду), более того, первая величина равна изменению второй, поэтому вместо импульса силы часто используют фразу "импульс тела", хотя более правильно говорить "изменение количества движения".

Силы, зависящие и не зависящие от времени

Выше закон импульса силы был представлен в дифференциальной форме. Чтобы посчитать значение этой величины, необходимо провести интегрирование по времени действия. Тогда получаем формулу:

∫ t1 t2 F¯(t)*dt = Δp¯

Здесь сила F¯(t) действует на тело в течение времени Δt = t2-t1, что приводит к изменению количества движения на Δp¯. Как видно, импульс силы - это величина, определяемая силой, зависящей от времени.

Теперь рассмотрим более простую ситуацию, которая реализуется в ряде экспериментальных случаев: будем считать, что сила от времени не зависит, тогда можно легко взять интеграл и получить простую формулу:

F¯*∫ t1 t2 dt = Δp¯ => F¯*(t2-t1) = Δp¯

При решении реальных задач на изменение количества движения, несмотря на то, что сила в общем случае зависит от времени действия, ее полагают постоянной и вычисляют некоторую эффективную среднюю величину F¯.

Примеры проявления на практике импульса силы

Какую роль играет эта величина, проще всего понять на конкретных примерах из практики. Перед тем как их привести, выпишем еще раз соответствующую формулу:

Заметим, если Δp¯ - величина постоянная, тогда модуль импульса силы - это тоже константа, поэтому чем больше Δt, тем меньше F¯, и наоборот.

Теперь приведем конкретные примеры импульса силы в действии:

• Человек, который прыгает с любой высоты на землю, старается при приземлении согнуть ноги в коленях, тем самым он увеличивает время Δt воздействия поверхности земли (сила реакции опоры F¯), тем самым уменьшая ее силу.
• Боксер, отклоняя голову от удара, продлевает время контакта Δt перчатки соперника с его лицом, уменьшая ударную силу.
• Современные автомобили стараются конструировать таким образом, чтобы в случае их столкновения их корпус как можно сильнее деформировался (деформация - это процесс, развивающийся во времени, что приводит к значительному снижению силы столкновения и, как следствие, снижению рисков повреждения пассажиров).

Понятие о моменте силы и его импульсе

И импульс этого момента - это другие величины, отличные от рассмотренной выше, поскольку они касаются уже не линейного, а вращательного движения. Итак, момент силы M¯ определяется как векторное произведение плеча (расстояния от оси вращения до точки воздействия силы) на саму силу, то есть справедлива формула:

Момент силы отражает способность последней выполнить кручение системы вокруг оси. Например, если взяться за гаечный ключ подальше от гайки (большой рычаг d¯), то можно создать большой момент M¯, что позволит открутить гайку.

По аналогии с линейным случаем импульс M¯ можно получить, умножив его на промежуток времени, в течение которого он воздействует на вращающуюся систему, то есть:

Величина ΔL¯ носит название изменения углового момента, или момента импульса. Последнее уравнение имеет важное значение для рассмотрения систем с осью вращения, ведь оно показывает, что момент импульса системы будет сохраняться, если отсутствуют внешние силы, создающие момент M¯, что математически записывается так:

Если M¯= 0, тогда L¯ = const

Таким образом, оба уравнения импульсов (для линейного и кругового движения) оказываются аналогичными в плане их физического смысла и математических следствий.

Задача на столкновение птицы и самолета

Эта проблема не является чем-то фантастическим. Такие столкновения действительно происходят довольно часто. Так, по некоторым данным в 1972 году на территории воздушного пространства Израиля (зона наиболее плотной миграции птиц) было зарегистрировано около 2,5 тысяч столкновений птиц с боевыми и транспортными самолетами, а также с вертолетами.

Задача заключается в следующем: необходимо приблизительно рассчитать, какая сила удара приходится на птицу, если на пути ее движения встречается самолет, летящий со скоростью v=800 км/ч.

Перед тем как приступать к решению, примем, что длина птицы в полете составляет l = 0,5 метра, а ее масса равна m = 4 кг (это может быть, например, селезень или гусь).

Пренебрежем скоростью движения птицы (она мала в сравнении с таковой для самолета), а также будем считать массу самолета намного большей, чем птицы. Эти приближения позволяют говорить, что изменение количества движения птицы равно:

Для вычисления силы удара F необходимо знать продолжительность этого инцидента, она приблизительно равна:

Комбинируя эти две формулы, получаем искомое выражение:

F = Δp/Δt = m*v 2 /l.

Подставив в него цифры из условия задачи, получаем F = 395062 Н.

Более наглядно будет перевести эту цифру в эквивалентную массу, используя формулу для веса тела. Тогда получим: F = 395062/9,81 ≈ 40 тонн! Иными словами птица воспринимает столкновение с самолетом так, будто на нее свалилось 40 тонн груза.

Любые задачи на движущиеся тела в классической механике требуют знания концепции импульса. В данной статье рассматривается эта концепция, дается ответ на вопрос, куда направлен вектор импульса тела, а также приводится пример решения задачи.

Количество движения

Чтобы выяснить, куда направлен вектор импульса тела, следует, в первую очередь, понять его физический смысл. Впервые термин был объяснен Исааком Ньютоном, однако важно отметить, что итальянский ученый Галилео Галилей в своих работах уже использовал похожее понятие. Для характеристики движущегося объекта он ввел величину, которая называлась стремление, натиск или собственно импульс (impeto на итальянском). Заслуга же Исаака Ньютона заключается в том, что он смог связать эту характеристику с действующими на тело силами.

Итак, изначально и более правильно то, что большинство понимают под импульсом тела, называть количеством движения. Действительно, математическая формула для рассматриваемой величины пишется в виде:

Здесь m - масса тела, v¯ - его скорость. Как видно из формулы, ни о каком импульсе речь не идет, имеется лишь скорость тела и его масса, то есть количество движения.

Важно отметить, что эта формула не следует из математических доказательств или выражений. Ее возникновение в физике имеет исключительно интуитивный, бытовой характер. Так, любой человек хорошо представляет, что если муха и грузовик будут двигаться с одинаковой скоростью, то грузовик остановить гораздо тяжелее, поскольку он обладает намного большим количеством движения, чем насекомое.

Откуда возникло понятие вектор импульса тела, рассмотрено далее.

Импульс силы - причина изменения количества движения

Интуитивно введенную характеристику Ньютон смог связать со вторым законом, носящим его фамилию.

Импульс силы - это известная физическая величина, которая равна произведению приложенной внешней силы к некоторому телу на время ее действия. Воспользовавшись известным законом Ньютона и полагая, что сила от времени не зависит, можно прийти к выражению:

F¯ * Δt = m * a¯ * Δt.

Здесь Δt - время действия силы F, a - это линейное ускорение, сообщаемое силой F телу массой m. Как известно, умножение ускорения тела на промежуток времени, который оно действует, дает приращение скорости. Этот факт позволяет переписать формулу выше в несколько ином виде:

F¯ * Δt = m * Δv¯, где Δv¯= a¯ * Δt.

Правая часть равенства представляет собой изменение количества движения (см. выражение в предыдущем пункте). Тогда получится:

F¯ * Δt = Δp¯, где Δp¯ = m * Δv¯.

Таким образом, пользуясь законом Ньютона и понятием об импульсе силы, можно прийти к важному выводу: воздействие внешней силы на объект в течение некоторого времени приводит к изменению его количества движения.

Теперь становится понятным, почему количество движения принято называть импульсом, ведь его изменение совпадает с импульсом силы (слово "сила", как правило, опускают).

Векторная величина p¯

Над некоторыми величинами (F¯, v¯, a¯, p¯) стоит черта. Это означает, что речь идет о векторной характеристике. То есть количество движения так же, как и скорость, сила и ускорение, помимо абсолютной величины (модуля), описывается еще направлением.

Так как каждый вектор можно разложить на отдельные компоненты, то, пользуясь декартовой прямоугольной системой координат, можно записать следующие равенства:

1) p¯ = m * v¯;

2) p x = m * v x ; p y = m * v y ; p z = m * v z ;

3) |p¯| = √(p x 2 + p y 2 + p z 2).

Здесь 1-е выражение - это векторная форма представления количества движения, 2-й набор формул позволяет рассчитать каждую из компонентов импульса p¯, зная соответствующие компоненты скорости (индексы x, y, z говорят о проекции вектора на соответствующую ось координат). Наконец, 3-я формула позволяет вычислить длину вектора импульса (абсолютное значение величины) через его компоненты.

Куда направлен вектор импульса тела?

Рассмотрев понятие количества движения p¯ и его основные свойства, можно легко ответить на поставленный вопрос. Вектор импульса тела направлен так же, как и вектор линейной скорости. Действительно, из математики известно, что умножение вектора a¯ на число k приводит к образованию нового вектора b¯, обладающего следующими свойствами:

• его длина равна произведению числа на модуль исходного вектора, то есть |b¯| = k * |a¯|;
• он направлен так же, как исходный вектор, если k > 0, в противном случае он будет направлен противоположно a¯.

В данном случае роль вектора a¯ играет скорость v¯, импульс p¯ - это новый вектор b¯, а число k - это масса тела m. Поскольку последняя всегда является положительной (m>0), то, отвечая на вопрос: чему сонаправлен вектор импульса тела p¯, следует сказать, что он сонаправлен скорости v¯.

Вектор изменения количества движения

Интересно рассмотреть еще один похожий вопрос: куда направлен вектор изменения импульса тела, то есть Δp¯. Для ответа на него стоит использовать полученную выше формулу:

F¯ * Δt = m * Δv¯ = Δp¯.

Исходя из рассуждений в предыдущем пункте, можно сказать, что направление изменения количества движения Δp¯ совпадает с направлением вектора силы F¯ (Δt > 0) или с направлением вектора изменения скорости Δv¯ (m > 0).

Здесь важно не путать, что речь идет именно об изменении величин. В общем случае векторы p¯ и Δp¯ не совпадают, поскольку они никак не связаны друг с другом. Например, если сила F¯ будет действовать против скорости v¯ перемещения объекта, тогда p¯ и Δp¯ будут направлены в противоположные стороны.

Где важно учитывать векторный характер количества движения?

Рассмотренные выше вопросы: куда направлен вектор импульса тела и вектор его изменения, обусловлены не простым любопытством. Дело в том, что закон сохранения импульса p¯ выполняется для каждой его компоненты. То есть в наиболее полной форме он записывается так:

p x = m * v x ; p y = m * v y ; p z = m * v z .

Каждая компонента вектора p¯ сохраняет свое значение в системе взаимодействующих объектов, на которые не действуют внешние силы (Δp¯ = 0).

Как пользоваться этим законом и векторными представлениями величины p¯, чтобы решать задачи на взаимодействие (соударение) тел?

Задача с двумя шарами

На рисунке ниже изображены два шара разной массы, которые летят под разными углами к горизонтальной линии. Пусть массы шаров равны m 1 = 1 кг, m 2 = 0,5 кг, их скорости v 1 = 2 м/с, v 2 = 3 м/с. Необходимо определить направление импульса после удара шаров, полагая последний абсолютно неупругим.

Начиная решать задачу, следует записать закон неизменности количества движения в векторной форме, то есть:

p 1 ¯ + p 2 ¯ = const.

Поскольку каждая компонента импульса должна сохраняться, то нужно переписать это выражение, учитывая также, что после столкновения два шара начнут двигаться, как единый объект (абсолютно неупругий удар):

m 1 * v 1x + m 2 * v 2x = (m 1 + m 2) * u x ;

M 1 * v 1y + m 2 * v 2y = (m 1 + m 2) * u y .

Знак минус для проекции импульса первого тела на ось y появился вследствие ее направленности против выбранного вектора оси ординат (см. рис.).

Теперь нужно выразить неизвестные компоненты скорости u, а затем подставить известные значения в выражения (соответствующие проекции скоростей определяются умножением модулей векторов v 1 ¯ и v 2 ¯ на тригонометрические функции):

u x = (m 1 * v 1x + m 2 * v 2x) / (m 1 + m 2), v 1x = v 1 * cos(45 o); v 2x = v 2 * cos(30 o);

u x = (1 * 2 * 0,7071 + 0,5 * 3 * 0,866) / (1 + 0,5) = 1,8088 м/с;

u y = (-m 1 * v 1y + m 2 * v 2y) / (m 1 + m 2), v 1y = v 1 * sin(45 o); v 2y = v 2 * sin(30 o);

u y = (-1 * 2 * 0,7071 + 0,5 * 3 * 0,5) / (1 + 0,5) = -0,4428 м/с.

Это две компоненты скорости тела после удара и "слипания" шаров. Поскольку направление скорости совпадает с вектором импульса p¯, то ответить на вопрос задачи можно, если определить u¯. Угол его относительно горизонтальной оси будет равен арктангенсу отношения компонент u y и u x:

α = arctg(-0,4428 / 1,8088) = -13,756 o .

Знак минус указывает, что импульс (скорость) после удара будет направлен вниз от оси x.