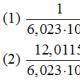"Eşek köprüsü" Pisagor teoreminin kanıtı, Orta Çağ öğrencilerinin çevrelerinde çok zor kabul edildi ve bazen Pons Asinorum "eşek köprüsü" veya elefuga - "yoksulların uçuşu" olarak adlandırıldı, çünkü bazı "fakir" öğrenciler, ciddi matematik eğitimi almamış, geometriden kaçmış. Teoremleri anlamadan ezberleyen ve bu nedenle "eşek" olarak adlandırılan zayıf öğrenciler, onlar için aşılmaz bir köprü görevi gören Pisagor teoremini aşamadılar.

Verilen: ABC, C = 90 °, B = 60 °, AB = 12 cm AC = 10 cm Bul: SABC Sözlü olarak çöz CA B Verilen: ABC, C = 90 °, AB = 18 cm, BC = 9 cm Bul: B , А Cevap: А = 30º, B = 60º Cevap: 30 cm²

C² = a 2 + b 2 a b c C A B c = a 2 + b cba Dik açılı bir üçgende a ve b bacaklardır, c hipotenüstür. Masayı doldurun. b = c²-a² a = c²-b² b 2 = c²-a² a 2 = c²-b²

Çözüm 3. ACD dikdörtgen, D = 45 ° DAC = 45 ° ACD - ikizkenar CD = AC = 4 SADC = 8. Yani tüm şeklin alanı S ABCB = SABC + SADC = Verilen: AB = 2 3, BC = 2, B = 90 ACD = 90 BAC = 3 0, D = 45 Bul: S ABCB. Problem 30º D С B A Tüm şeklin alanı S ABCB = SABC + SADC 2. ABC dikdörtgen, SABC = 2 3; BAC = 30 ° AC = 2BC = 4.

497 Paralelkenarın köşegenlerinden biri yüksekliğidir. Paralelkenar çevresi 50 cm ve bitişik kenarlar arasındaki fark 1 cm ise bu köşegeni bulun AD CB Verilen: ABCD - paralelkenar, BD AD, P ABCD = 50 cm, AB-AD = 1 cm Bulun: BD. Çözüm. AD = x cm, sonra AB = (x + 1) görelim. P ABCD = 2 (AB + AD), sonra 50 = 2 (x + 1 + x) 25 = 2x + 1 x = 12, sonra AD = 12 cm, AB = 13 cm 1. AD = 12 cm AB = 13 2. Pisagor teoremini kullanarak BD'yi bulun: AB² = BD² + AD² BD = 5 (cm) 12 cm 13 cm

BC 6 cm Bul: BC, CD, AD. "title =" (! LANG: Problem Dikdörtgen bir yamuğun alanı 120 cm² ve ​​yüksekliği 8 cm'dir. Tabanlarından biri diğerinden 6 cm büyükse yamuğun tüm kenarlarını bulun. D BC AN Verilen : ABCD - yamuk, AB AD , S ABCD = 120 cm², AB = 8 cm, AD> BC 6 cm Bul: BC, CD, AD." class="link_thumb"> 16 !} Problem Dikdörtgen bir yamuğun alanı 120 cm² ve ​​yüksekliği 8 cm'dir.Tabanlarından biri diğerinden 6 cm daha büyükse yamuğun tüm kenarlarını bulun. D BC A N Verilen: ABCD - yamuk, AB AD, S ABCD = 120 cm², AB = 8 cm, AD> BC 6 cm Bul: BC, CD, AD. Çözüm. BC = x cm, sonra AD = (x + 6) cm olsun. S ABCD = 8 (x + 6 + x) = 120, 4 (2x + 6) = 120 2x + 6 = 30 x = 12, yani BC 12 cm, AD = 18 cm AB = 8 cm, BC = 12 cm, AD = 18 cm Ek yapı: CH AD, o zaman ABCH bir dikdörtgendir. CH = AB = 8 cm, AH = BC = 12 cm, sonra HD = AD-AH = 6 cm 12 cm 18 cm 6 cm CD'yi Pisagor teoremine göre bulun: CD² = CH² + HD² CD = 8² + 6² CD = 10 ( cm) Cevap: AB = 8 cm, BC = 12 cm, CD = 10 cm, AD = 18 cm. BC 6 cm Bul: BC, CD, AD. "> BC 6 cm. Bul: BC, CD, AD. Çözüm. BC = x cm olsun, sonra AD = (x + 6) cm Çünkü S ABCD = · 8 · (x + 6 + x) = 120, 4 (2x + 6) = 120 2x + 6 = 30x = 12, yani BC 12 cm, AD = 18 cm 1.2 AB = 8 cm, BC = 12 cm, AD = 18 cm Ek yapı: CH AD, sonra ABCH dikdörtgen CH = AB = 8 cm, AH = BC = 12 cm, sonra HD = AD-AH = 6 cm 12 cm 18 cm 6 cm CD'yi Pisagor teoremine göre bulun: CD² = CH² + HD² CD = 8² + 6²СD = 10 ( cm) Cevap: AB = 8 cm, BC = 12 cm, СD = 10 cm, AD = 18 cm. "> BC 6 cm. Bul: BC, CD, AD. "title =" (! LANG: Problem Dikdörtgen bir yamuğun alanı 120 cm² ve ​​yüksekliği 8 cm'dir. Tabanlarından biri diğerinden 6 cm büyükse yamuğun tüm kenarlarını bulun. D BC AN Verilen : ABCD - yamuk, AB AD , S ABCD = 120 cm², AB = 8 cm, AD> BC 6 cm Bul: BC, CD, AD."> title="Problem Dikdörtgen bir yamuğun alanı 120 cm² ve ​​yüksekliği 8 cm'dir.Tabanlarından biri diğerinden 6 cm daha büyükse yamuğun tüm kenarlarını bulun. D BC A N Verilen: ABCD - yamuk, AB AD, S ABCD = 120 cm², AB = 8 cm, AD> BC 6 cm Bul: BC, CD, AD."> !} AB C M N Verilen: ABC, BC = 7,5 cm, AC = 3,2 cm, AM BC, BN AC, AM = 2,4 cm Bul: BN Çözüm: SABC = ½AM · SV = ½ · 2,4 · 7,5 = 9 cm² S ABC = ½BN · AC BN = 2 · S ABC: AC = 2 · 9: 3.2 = 5.625 cm Cevap: 5.625 cm Üçgenin iki kenarı 7.5 cm ve 4 cm Büyük kenarın yüksekliği 2.4 cm'dir. verilen kenarlardan daha küçüktür. 470

Meydan sağ üçgen 168 cm²'ye eşittir. Uzunluklarının oranı 7:12 ise bacaklarını bulun. А С В Verilen: ABC, С = 90º, AC: ВС = 7: 12, S ABC = 168 cm² Bul: АС, BC. Çözüm: SABC = ½АС · ВС 168 = ½7х · 12х 168 = 42х² х = 2 АС = 14 cm, ВС = 24 cm Cevap: 14 cm ve 24 cm 472

Alan özellikleri 10. Eşit çokgenlerin alanları eşittir. D B A C N ABC = NFD F

Alanların özellikleri 20. Bir çokgen birkaç çokgenden oluşuyorsa, alanı bu çokgenlerin alanlarının toplamına eşittir. C B D A F

Alanların özellikleri 30. Bir karenin alanı, kenarının karesine eşittir. 3 cm S = 9 cm 2 Alanların özelliklerini kullanarak şekillerin alanlarını bulunuz

Alan ölçü birimleri 1 m 2 = 100 dm 2 1 dm 2 = 100 cm 2

Alan ölçü birimleri 1 km 2 1 ha 1 a 1 m 2 1 dm 2 1 cm 2 1 mm 2: 100: 100

Bir dikdörtgenin alanı b S S = ab aa KENAR İLE KARE a 2 a + b = S + a 2 + b 2 a 2 +2 ab + b 2 = 2 S + a 2 + b 2 S (a + b) 2 S 2 ab = 2 SS = ab b 2 b: 2

Kenarları 5, 5 m ve 6 m olan dikdörtgen şeklindeki odanın zemini dikdörtgen parke ile kaplanmalıdır. Her bir parke tahtasının uzunluğu 30 cm ve genişliği 5 cm'dir.Zemini kaplamak için kaç tane tahta gerekir? 6 m 5.5 m 5 cm 30 cm

Dikdörtgenin kenarlarına kurulan karelerin alanları 64 cm 2 ve 121 cm 2'dir. Dikdörtgenin alanını bulunuz. 121 cm 2 S-? 64 cm2

ABCD ve ARMC dikdörtgenlerinin her birinin kenarları 6 cm ve 10 cm'dir.Bu dikdörtgenlerden en az birine ait olan tüm noktalardan oluşan bir şeklin alanını bulun. A 10 cm P B 6 cm 10 cm D K C 6 cm M

ABCD dikdörtgeni, AC - köşegen. ABC üçgeninin alanını bulun. A a D ABC = ADC b SABC = B C

ABCD bir dikdörtgendir. Bul: SABF. B CE = DE, C F E A D SABCD = Q

AB = BC = 3, AF = 5, Bul: SABCDEF. B EF = 2.C 3 D E 3 A 2 5 F

S = 102 C K, M, T ve E noktaları sırasıyla E ABCD karesinin AD, AB, BC ve DC taraflarında KD = 7, AK = 3, AM = 5, BT = 8 olacak şekilde 5 bulunur, CE = 5. KMTE dörtgeninin alanını bulun. D T B 2 8 M 5 7 K 3 A

ABCD beşgeninin alanı 48 cm2'dir. ABCD karesinin alanını ve çevresini bulun. C B O A 1) 48: 3 * 4 = 64 (cm 2) SABSD 2) AB = 8 (cm), PABSD = 8 * 4 = 32 (cm) D

ABCD ve MDKP eşit karelerdir. AB = 8 cm ASKM dörtgeninin alanını bulun. B C 64 cm 2 8 cm 32 cm 2 D A 32 cm 2 M K 32 cm 2 R

ABCD ve DCMK karelerdir. AB = 6 cm OCPD dörtgeninin alanını bulun. CH 6 cm A O M P D K

ABCD - dikdörtgen; M, K, P, T - kenarlarının ortası, AB = 6 cm, AD = 12 cm MKRT dörtgeninin alanını bulun. B K 6 cm M A C P T 12 cm D

ABCD - dikdörtgen; M, K, P, T - kenarlarının ortası, AB = 16 cm, BC = 10 cm.AMKSRT altıgen alanını bulun. C P 10 cm K B D T M 16 cm A

Görev Kaynağı: Karar 2746.-13. OGE 2017 Matematik, I.V. Yaşçenko. 36 seçenek.

Görev 11. Eşkenar dörtgenin kenarı 12'dir ve eşkenar dörtgenin köşegenlerinin kesişme noktasından ona olan uzaklık 1'dir. Bu eşkenar dörtgenin alanını bulun.

Çözüm.

Bir eşkenar dörtgenin alanı, bir paralelkenarın alanı ile aynı şekilde hesaplanabilir, yani eşkenar dörtgenin h yüksekliğinin, çizildiği a kenarının uzunluğu ile çarpımı olarak:

Şekilde kırmızı çizgi siyah çizgi ile birlikte eşkenar dörtgenin (siyah ve kırmızı çizgilerin uzunlukları eşit olduğundan) eşit olan h yüksekliğini göstermektedir. Kenar uzunluğu a = 12 de problem ifadesine göre. Eşkenar dörtgen alanını alıyoruz:

Cevap: 24.

Görev 12. 1x1 kareli kağıda bir eşkenar dörtgen tasvir edilmiştir. Büyük köşegeninin uzunluğunu bulun.

Çözüm.

Şekilde mavi çizgiler eşkenar dörtgenin köşegenlerini göstermektedir. Büyük köşegenin 12 hücre olduğu görülebilir.

Cevap: 12.

Görev 13. Aşağıdaki ifadelerden hangileri doğrudur?

1) Köşegenleri birbirine dik olan bir dikdörtgen var.

2) Tüm karelerin alanları eşittir.

3) Üçgenin açılarından biri her zaman 60 dereceyi geçmez.

Yanıt olarak, seçtiğiniz ifadelerin numaralarını boşluk, virgül veya diğer ek karakterler olmadan yazın.

Çözüm.

1) Doğru. Bu, kareye dönüşen bir dikdörtgendir.

VIII sınıf: Konu 3. Şekillerin kareleri. Pisagor teoremi.

1. Alan kavramı. Eşit boyutlu rakamlar.

Uzunluk bir çizginin sayısal bir özelliğiyse, alan kapalı bir şeklin sayısal bir özelliğidir. Alan kavramına aşina olmamıza rağmen, Gündelik Yaşam, bu kavrama kesin bir tanım vermek kolay değildir. Kapalı bir şeklin alanının aşağıdakilerle negatif olmayan herhangi bir miktar olarak adlandırılabileceği ortaya çıktı. şekillerin alanlarını ölçmenin özellikleri:

Eşit parçalar eşit alanlara sahiptir. Bu kapalı şekil birkaç kapalı şekle bölünürse, şeklin alanı, onu oluşturan şekillerin alanlarının toplamına eşittir (Şekil 1'deki şekil, n rakamlar; bu durumda, şeklin alanı, nerede Si- Meydan ben-inci rakam).

Prensip olarak, formüle edilmiş özelliklere sahip bir dizi miktar bulmak ve bu nedenle şeklin alanını karakterize etmek mümkün olacaktır. Ancak en tanıdık ve kullanışlı olanı, bir karenin alanını, kenarının karesi olarak karakterize eden değerdir. Bu "düzenleme", şekillerin alanlarını ölçmenin üçüncü özelliği olarak adlandıralım:

Bir karenin alanı, kenarının karesine eşittir (Şekil 2).

Bu tanım ile şekillerin alanı ölçülmektedir. kare birimler (santimetre 2, km 2, Ha=100m 2).

şekiller eşit alanlara sahip denir eşit .

Yorum Yap: Eşit rakamlar eşit alanlara sahiptir, yani eşit rakamlar eşit alanlar. Ancak eşit büyüklükteki rakamlar her zaman eşit olmaktan uzaktır (örneğin, şekil 3, eşit dik açılı üçgenlerden oluşan bir kare ve ikizkenar üçgeni gösterir (bu arada, rakamlar arandı eşit ); kare ve üçgenin boyut olarak eşit olduğu, ancak örtüşmedikleri için eşit olmadığı açıktır).

Daha sonra, şekillerin alanlarını ölçmenin formüle edilmiş özelliklerine dayanarak, tüm temel çokgen türlerinin (bir dikdörtgenin alanını bulmak için iyi bilinen formül dahil) alanlarını hesaplamak için formüller türetiyoruz.

2. Dikdörtgenin alanı. Paralelkenar alanı.

Bir dikdörtgenin alanını hesaplamak için formül: Dikdörtgenin alanı, bitişik iki kenarının ürününe eşittir (Şekil 4).

Verilen:

ABCD- dikdörtgen;

AD=a, AB=B.

İspat et: SABCD=a× B.

Kanıt:

1. Kenarı uzatın AB segment başına BP=a ve yan AD- segment başına DVD=B... Paralelkenar yapalım APRV(Şekil 4). l'den beri A= 90 °, APRV- dikdörtgen. nerede AP=a+B=AV, Þ APRV- kenarlı kare ( a+B).

2. Belirtmek M.ÖÇ karavan=T, CDÇ halkla ilişkiler=Q... Sonra BCQP- yan kare a, CDVT- yan kare B, CQRT- kenarları olan dikdörtgen a ve B.

Bir paralelkenarın alanını hesaplamak için formül: Paralelkenarın alanı, yüksekliğinin ve tabanının ürününe eşittir (Şekil 5).

Yorum Yap: Paralelkenarın tabanına genellikle yüksekliğin çizildiği taraf denir; paralelkenarın her iki tarafının da taban görevi görebileceği açıktır.

Verilen:

ABCD- p / g;

BH^AD, HÎ AD.

İspat et: SABCD=AD× BH.

Kanıt:

1. Üsse gidelim AD yükseklik CF(Şekil 5).

2. M.Öïê HF, BHïê CF, Þ BCFH- tanım gereği p / g. NS H= 90 °, Þ BCFH- dikdörtgen.

3. BCFH- p / g, Þ özelliğine göre p / g BH=CF, ÞD BAH= D CDF hipotenüs ve bacak boyunca ( AB=CD sv-woo p / g'de, BH=CF).

4. SABCD=SABCF+S NS CDF=SABCF+S NS BAH=SBCFH=BH× M.Ö=BH× AD. #

3. Bir üçgenin alanı.

Bir üçgenin alanını hesaplamak için formül: Bir üçgenin alanı, yüksekliğinin ve tabanının çarpımının yarısına eşittir (Şekil 6).

Yorum Yap: Bu durumda üçgenin tabanı, yüksekliğin çizildiği taraftır. Bir üçgenin üç kenarından herhangi biri, onun tabanı olarak hizmet edebilir.

Verilen:

BD^AC, NSÎ AC.

İspat et: .

Kanıt:

1. D'yi bitirelim ABC p / y'ye kadar ABKCüstten geçerek B Düz BKïê AC, ve üstten C- Düz CKïê AB(Şekil 6).

2. NS ABC= D KKHüç tarafta ( M.Ö- Genel, AB=KK ve AC=KB sv-vu p / g'de), Þ https://pandia.ru/text/78/214/images/image014_34.gif "width =" 107 "height =" 36 ">).

Sonuç 2: p / y D'yi düşünürsek ABC yükseklik ile AH hipotenüse çizilmiş M.Ö, sonra . Böylece, p / y'de D-ke hipotenüse çizilen yükseklik, bacaklarının çarpımının hipotenüse oranına eşittir ... Bu oran genellikle problem çözerken kullanılır.

4. Bir üçgenin alanını bulma formülünden elde edilen sonuçlar: eşit yüksekliklere veya tabanlara sahip üçgen alanlarının oranı; şekillerde eşit alan üçgenleri; dışbükey bir dörtgenin köşegenlerinin oluşturduğu üçgen alanlarının özelliği.

Bir üçgenin alanını hesaplama formülünden temel olarak iki sonuç çıkar:

1. Yükseklikleri eşit olan üçgenlerin alanlarının oranı tabanlarının oranına eşittir (Şekil 8'de ).

2. Tabanları eşit olan üçgenlerin alanlarının oranı yüksekliklerinin oranına eşittir (Şekil 9'da ).

Yorum Yap: Problemleri çözerken, toplam yüksekliğe sahip üçgenlere çok sık rastlanır. Ayrıca, bir kural olarak, tabanları bir düz çizgi üzerinde uzanır ve tabanların karşısındaki üst kısım yaygındır (örneğin, Şekil 10'da). S 1:S 2:S 3=a:B:C). Bu tür üçgenlerin toplam yüksekliğini görmeyi öğrenmelisiniz.

Ayrıca bir üçgenin alanını hesaplama formülünden faydalı gerçekler bulmanızı sağlayan şekillerde eşit alan üçgenleri:

1. Rasgele bir üçgenin medyanı onu iki eşit üçgene böler (Şekil 11, D'de ABM ve D ACM boy uzunluğu AH- genel ve temel BM ve SANTİMETRE medyanın tanımına göre eşit; bunu nereden takip ediyor D ABM ve D ACM eşit alanlar).

2. Paralelkenarın köşegenleri onu dört eşit üçgene böler (Şekil 12'de AOüçgenin medyanı mı ABD köşegenlerin özelliği ile n / r, Þ önceki sv-va üçgenleri sayesinde ABO ve ADO eşit alanlar; t. için. BÖüçgenin medyanı mı ABC, üçgenler ABO ve BCO eşit alanlar; t. için. COüçgenin medyanı mı BCD, üçgenler BCO ve DCO eşit alanlar; Böylece, S NS ADO=S NS ABO=S NS BCO=S NS DCO).

3. Yamuğun köşegenleri onu dört üçgene böler; yanlara bitişik iki tanesi eşittir (Şekil 13).

Verilen:

ABCD- yamuk;

M.Öïê AD; ACÇ BD=Ö.

İspat et: S NS ABO=S NS DCO.

Kanıt:

1. Yükseklikleri koruyalım erkek arkadaş ve CH(Şekil 13). sonra D ABD ve D AKD temel AD- genel ve yükseklikler erkek arkadaş ve CH eşittir; NS S NS ABD=S NS AKD.

2. S NS ABO=S NS ABD ‑ S NS AOD=S NS AKD ‑ S NS AOD=S NS DCO. #

Bir dışbükey dörtgenin köşegenlerini çizerseniz (Şekil 14), alanları hatırlaması çok kolay bir oranla birbirine bağlanan dört üçgen oluşur. Bu oranın türetilmesi yalnızca bir üçgenin alanını hesaplama formülüne dayanmaktadır; ancak literatürde nadirdir. Sorunların çözümünde faydalı olmakla birlikte, aşağıda formüle edilecek ve kanıtlanacak olan ilişki yakın ilgiyi hak ediyor:

Dışbükey bir dörtgenin köşegenlerinin oluşturduğu üçgen alanlarının özelliği: Dışbükey bir dörtgenin köşegenleri ise ABCD noktada kesişmek Ö, ardından (Şekil 14).

ABCD- dışbükey dörtgen;

https://pandia.ru/text/78/214/images/image025_28.gif "width =" 149 "height =" 20 ">.

Kanıt:

1. erkek arkadaş- toplam yükseklik D AOB ve D BOC; Þ S NS AOB:S NS BOC=AO:CO.

2. DH- toplam yükseklik D AOD ve D MORİNA; Þ S NS AOD:S NS MORİNA=AO:CO.

5. Açıları eşit olan üçgenlerin alanlarının oranı.

Açıları eşit olan üçgenlerin alanlarının oranı ile ilgili teorem: Açıları eşit olan üçgenlerin alanları, bu açıları çevreleyen kenarların çarpımı olarak adlandırılır (Şekil 15).

verilen:

NS ABC, NS A 1B 1C 1;

Ð BAC=Ð B 1A 1C 1.

İspat et:

.

Kanıt:

1. Işını bir kenara koyun AB Bölüm AB 2=A 1B 1 ve kiriş üzerinde AC- Bölüm AC 2=A 1C 1 (Şekil 15). sonra D AB 2C 2 = D A 1B 1C Her iki tarafta 1 ve aralarındaki köşe ( AB 2=A 1B 1 ve AC 2=A 1C 1 inşaat ve l B 2AC 2 = P B 1A 1C 1 koşula göre). Anlamına geliyor, .

2. Noktaları birleştirin C ve B 2.

3. CH- toplam yükseklik D AB 2C ve D ABC, Þ https://pandia.ru/text/78/214/images/image033_22.gif "width =" 81 "height =" 43 src = ">.

6. Bir üçgenin bisektörünün özelliği.

Eşit açılara sahip üçgenlerin alanlarının oranı ve eşit yükseklikteki üçgenlerin alanlarının oranı üzerine teoremleri kullanarak, basitçe, şekillerin alanlarıyla doğrudan ilişkisi olmayan problemlerin çözümünde son derece yararlı olan bir gerçeği kanıtlıyoruz:

Üçgen bisektör özelliği: Bir üçgenin açıortay çizildiği tarafı bitişik taraflarla orantılı parçalara böler.

Verilen:

https://pandia.ru/text/78/214/images/image036_22.gif "width =" 61 "height =" 37 ">.

Kanıt:

1..gif "genişlik =" 72 yükseklik = 40 "yükseklik =" 40 ">.

3. 1. ve 2. noktalardan şunu elde ederiz: , Þ https://pandia.ru/text/78/214/images/image041_19.gif "width =" 61 "height =" 37 ">. #

Yorum Yap: Uç terimler veya orta terimler doğru orantıda yer değiştirilebildiğinden, bir üçgenin açıortay özelliğini aşağıdaki biçimde hatırlamak daha uygundur (Şekil 16):

7. Yamuğun alanı.

Bir yamuğun alanını hesaplamak için formül: Yamuğun alanı, tabanların yarısı ile yüksekliğinin çarpımına eşittir.

Verilen:

ABCD- yamuk;

M.Öïê AD;

BH- boy uzunluğu.

https://pandia.ru/text/78/214/images/image044_21.gif "width =" 127 "height =" 36 ">.

Kanıt:

1. Bir köşegen çizin BD ve yükseklik DF(Şekil 17). bhdf- dikdörtgen, Þ BH = DF.

Sonuç: Eşit yükseklikteki yamuk alanlarının oranı, orta hatlarının oranına (veya tabanların toplamlarının oranına) eşittir.

8. Karşılıklı dik köşegenlere sahip bir dörtgen alanı.

Karşılıklı olarak dik köşegenleri olan bir dörtgenin alanını hesaplamak için formül: Köşegenleri birbirine dik olan bir dörtgenin alanı, köşegenlerinin çarpımının yarısına eşittir.

ABCD- bir dörtgen;

AC^BD.

https://pandia.ru/text/78/214/images/image049_20.gif "width =" 104 "height =" 36 ">.

Kanıt:

1. Belirtmek ACÇ BD=Ö... kadarıyla AC^BD, AO- yükseklik D ABD, a CO- yükseklik D MİA(Dışbükey ve dışbükey olmayan dörtgenler için sırasıyla Şekil 18a ve 18b).

2.
("+" veya "-" işaretleri, sırasıyla dışbükey ve dışbükey olmayan dörtgen durumlarına karşılık gelir). #

Pisagor teoremi, çok çeşitli problemlerin çözümünde son derece önemli bir rol oynar; bir dik üçgenin bilinmeyen tarafını bilinen iki tarafından bulmanızı sağlar. Pisagor teoreminin bilinen birçok ispatı vardır. İşte bir kare ve bir üçgenin alanlarını hesaplamak için formüllere dayanan en basitleri:

Pisagor teoremi: Dik açılı bir üçgende hipotenüsün karesi, bacakların karelerinin toplamına eşittir.

Verilen:

NS ABC- yok;

Ð A= 90 °.

İspat et:

M.Ö 2=AB 2+AC 2.

Kanıt:

1. Belirtmek AC=a, AB=B... Işın üzerinde bir kenara koyun AB Bölüm BP=a, ve ışın üzerinde AC- Bölüm Özgeçmiş=B(Şekil 19). Noktayı çizelim P Düz halkla ilişkilerïê AV, ve nokta aracılığıyla V- Düz sanal gerçeklikïê AP... Sonra APRV- tanımı gereği p / g. Ayrıca, l'den beri A= 90 °, APRV- dikdörtgen. Dan beri. AV=a+B=AP, APRV- yan kare a+B, ve SAPRV=(a+B) 2. Sonra, tarafı bölelim halkla ilişkiler puan Q segmentler için PQ=B ve QR=a ve yan karavan- puan T segmentler için RT=B ve televizyon=a.

2. D ABC= D PQB= D RTQ= D VCT iki ayak üzerinde, Þ Ð ACB=Ð PBQ=Ð RQT=Ð VTC, M.Ö=QB=TQ=BT ve https://pandia.ru/text/78/214/images/image055_17.gif "width =" 115 "height =" 36 ">.

3.T. M.Ö=QB=TQ=BT, CBQT- eşkenar dörtgen. Ayrıca, ben QBC= 180 ° - (Ð ABC+Ð PBQ) = 180 ° - (P ABC+Ð ACB)=Ð BAC= 90 °; NS CBQT- kare ve SCBQT=M.Ö 2.

4. . Yani, M.Ö 2=AB 2+AC 2. #

Ters Pisagor teoremi, dik açılı bir üçgenin işaretidir, yani üçe izin verir. bilinen taraflar dikdörtgen olup olmadığını kontrol etmek için üçgen.

Ters Pisagor teoremi: Bir üçgenin bir kenarının karesi, diğer iki kenarının karelerinin toplamına eşitse, bu üçgen dikdörtgendir ve büyük kenarı hipotenüstür.

Verilen:

M.Ö 2=AB 2+AC 2.

İspat et: NS ABC- yok;

Ð A= 90 °.

Kanıt:

1. Bir dik açı oluşturalım A 1 ve yanlarında segmentleri erteliyoruz A 1B 1=AB ve A 1C 1=AC(Şekil 20). Alınan p / y D'de A 1B 1C 1 Pisagor teoremi ile B 1C 12=A 1B 12+A 1C 12=AB 2+AC 2; ama koşula göre AB 2+AC 2=M.Ö 2; NS B 1C 12=M.Ö 2, Þ B 1C 1=M.Ö.

2. D ABC= D A 1B 1CÜç tarafta 1 ( A 1B 1=AB ve A 1C 1=AC inşaat tarafından, B 1C 1=M.Ö madde 1), Þ l A=Ð A 1 = 90 °, ÞD ABC- yok. #

Kenar uzunlukları doğal sayılarla ifade edilen dikdörtgen üçgenlere denir. Pisagor üçgenleri , ve karşılık gelen üçlüler doğal sayılar – Pisagor üçüzleri ... Pisagor üçlülerini hatırlamakta fayda var (bu sayıların büyük olanı diğer ikisinin karelerinin toplamına eşittir). İşte bazı Pisagor üçüzleri:

3, 4, 5;

5, 12, 13;

8, 15, 17;

7, 24, 25;

20, 21, 29;

12, 35, 37;

9, 40, 41.

Mısır'da dik açıları oluşturmak için kenarları 3, 4, 5 olan dik açılı bir üçgen kullanıldı ve bu nedenle üçgen arandı Mısırlı .

10. Heron formülü.

Heron'un formülü, bilinen üç tarafı ile keyfi bir üçgenin alanını bulmanızı sağlar ve birçok sorunun çözümünde vazgeçilmezdir.

Heron'un formülü: Kenarları olan bir üçgenin alanı a, B ve C aşağıdaki formülle hesaplanır:, üçgenin yarı çevresi nerede.

verilen:

M.Ö=a; AC=B; AB=C.). Sonra .

4. Yükseklik için elde edilen ifadeyi bir üçgenin alanını hesaplamak için formülde değiştirin:. #