Sections of the site
Editor's Choice:
- Gender of nouns in English
- Beautiful phrases in English with translation: about love, quotes from songs, useful expressions Beautiful quotes in English with translation
- What sounds do German animals make
- What sounds do German animals make
- How to understand what level of English
- How many words are there in German
- English Trainer Audio Trainer for English Learning
- We talk on the phone in English - useful words and phrases
- Best quotes in English
- Topic Car, road - English for a driver Russian-English phrasebook for drivers meeting foreigners
Advertising
| The last activity is the addition of powers with the same bases. Addition rules. All of the above formulas are read and executed in both directions from left to right and vice versa |
|
We remind you that this lesson understands power properties with natural indicators and zero. Rational degrees and their properties will be covered in the 8th grade lessons. A natural exponent has several important properties that make it easier to calculate in exponent examples. Property number 1
|
| 2 5 |
| 2 5 |
Important!
Please note that in property 2 we were talking only about dividing degrees with the same bases.
You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if you count (4 3 −4 2) = (64 − 16) = 48 , and 4 1 = 4
Be careful!
Property number 3
Exponentiation
Remember!
When raising a power to a power, the base of the power remains unchanged, and the exponents are multiplied.
(a n) m = a n · m, where "a" is any number, and "m", "n" are any natural numbers.

Properties 4
Degree of work
Remember!
When raising to the power of a product, each of the factors is raised to a power. The results are then multiplied.
(a · b) n = a n · b n, where "a", "b" are any rational numbers; "N" is any natural number.
- Example 1.
(6 a 2 b 3 s) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2 - Example 2.
(−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6
Important!
Note that property # 4, like other power properties, is applied in reverse order.
(a n b n) = (a b) nThat is, in order to multiply degrees with the same indicators, you can multiply the bases, and the exponent can be left unchanged.
- Example. Calculate.
2 4 5 4 = (2 5) 4 = 10 4 = 10,000 - Example. Calculate.
0.5 16 2 16 = (0.5 2) 16 = 1
In more complex examples, there may be cases when multiplication and division must be performed over degrees with different bases and different exponents. In this case, we advise you to proceed as follows.
For example, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
An example of raising to a decimal power.
4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4Properties 5
Degree of quotient (fraction)
Remember!
To raise a quotient to a power, you can raise a separate dividend and a divisor to this power, and divide the first result by the second.
(a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n is any natural number.
- Example. Present the expression in the form of private degrees.
(5: 3) 12 = 5 12: 3 12
We remind you that the quotient can be represented as a fraction. Therefore, we will dwell on the topic of raising a fraction to a power in more detail on the next page.
How do you multiply degrees? Which degrees can be multiplied and which cannot? How to multiply a number by a degree?
In algebra, the product of degrees can be found in two cases:
1) if the degrees have the same bases;
2) if the degrees have the same indicators.
When multiplying degrees with the same bases, the base must be left the same, and the indicators must be added:
When multiplying degrees with the same indicators, the total indicator can be taken out of the brackets:
Let's look at how to multiply degrees using specific examples.
The unit in the exponent is not written, but when the degrees are multiplied, they take into account:
When multiplying, the number of degrees can be any. It should be remembered that you do not need to write the multiplication sign before the letter:
In expressions, exponentiation is performed first.
If you need to multiply a number by a power, you must first perform the exponentiation, and only then the multiplication:
www.algebraclass.ru
Addition, subtraction, multiplication, and division of powers
Add and subtract powers
Obviously, numbers with powers can be added, like other quantities , by adding them one by one with their signs.
So, the sum of a 3 and b 2 is a 3 + b 2.
The sum of a 3 - b n and h 5 -d 4 is a 3 - b n + h 5 - d 4.
Odds the same degrees of the same variables can be added or subtracted.
So, the sum of 2a 2 and 3a 2 is 5a 2.
It is also obvious that if you take two squares a, or three squares a, or five squares a.
But the degrees different variables and varying degrees identical variables, must be added by their addition with their signs.
So, the sum of a 2 and a 3 is the sum of a 2 + a 3.
It is obvious that the square of a, and the cube of a, is not equal to twice the square of a, but twice the cube of a.
The sum of a 3 b n and 3a 5 b 6 is a 3 b n + 3a 5 b 6.
Subtraction degrees is carried out in the same way as addition, except that the signs of the subtracted must be changed accordingly.
Or:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 - 4h 2 b 6 = -h 2 b 6
5 (a - h) 6 - 2 (a - h) 6 = 3 (a - h) 6
Multiplication of degrees
Numbers with powers can be multiplied, like other quantities, by writing them one after the other, with or without a multiplication sign between them.
So, the result of multiplying a 3 by b 2 is a 3 b 2 or aaabb.
Or:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y
The result in the last example can be ordered by adding the same variables.
The expression will take the form: a 5 b 5 y 3.
By comparing several numbers (variables) with powers, we can see that if any two of them are multiplied, then the result is a number (variable) with a power equal to the sum degrees of terms.
So, a 2 .a 3 = aa.aaa = aaaaa = a 5.
Here 5 is the power of the result of multiplication, equal to 2 + 3, the sum of the powers of the terms.
So, a n .a m = a m + n.
For a n, a is taken as a factor as many times as the power of n is equal;
And a m, is taken as a factor as many times as the power of m is;
That's why, degrees with the same stems can be multiplied by adding the exponents.
So, a 2 .a 6 = a 2 + 6 = a 8. And x 3 .x 2 .x = x 3 + 2 + 1 = x 6.
Or:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n + 1
Multiply (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Answer: x 4 - y 4.
Multiply (x 3 + x - 5) ⋅ (2x 3 + x + 1).
This rule is also true for numbers whose exponents are - negative.
1. So, a -2 .a -3 = a -5. This can be written as (1 / aa). (1 / aaa) = 1 / aaaaa.
2.y -n .y -m = y -n-m.
3.a -n .a m = a m-n.
If a + b is multiplied by a - b, the result is a 2 - b 2: that is
The result of multiplying the sum or difference of two numbers is equal to the sum or difference of their squares.
If the sum and difference of two numbers raised to square, the result will be equal to the sum or difference of these numbers in fourth degree.
So, (a - y). (A + y) = a 2 - y 2.
(a 2 - y 2) ⋅ (a 2 + y 2) = a 4 - y 4.
(a 4 - y 4) ⋅ (a 4 + y 4) = a 8 - y 8.
Division of degrees
Power numbers can be divided, like other numbers, by subtracting from the divisor, or by placing them in fractional form.
So a 3 b 2 divided by b 2 equals a 3.
A 5 divided by a 3 looks like $ \ frac $. But this is equal to a 2. In a series of numbers
a +4, a +3, a +2, a +1, a 0, a -1, a -2, a -3, a -4.
any number can be divided by another, and the exponent will be equal to difference exponents of divisible numbers.
When dividing degrees with the same base, their indicators are subtracted..
So, y 3: y 2 = y 3-2 = y 1. That is, $ \ frac = y $.
And a n + 1: a = a n + 1-1 = a n. That is, $ \ frac = a ^ n $.
Or:
y 2m: y m = y m
8a n + m: 4a m = 2a n
12 (b + y) n: 3 (b + y) 3 = 4 (b + y) n-3
The rule is also true for numbers with negative the values of the degrees.
The result of dividing a -5 by a -3 is a -2.
Also, $ \ frac: \ frac = \ frac. \ Frac = \ frac = \ frac $.
h 2: h -1 = h 2 + 1 = h 3 or $ h ^ 2: \ frac = h ^ 2. \ frac = h ^ 3 $
It is necessary to master multiplication and division of powers very well, since such operations are very widely used in algebra.
Examples of solving examples with fractions containing numbers with powers
1. Decrease exponents in $ \ frac $ Answer: $ \ frac $.
2. Decrease exponents in $ \ frac $. Answer: $ \ frac $ or 2x.
3. Decrease the exponents a 2 / a 3 and a -3 / a -4 and bring them to the common denominator.
a 2 .a -4 is a -2 first numerator.
a 3 .a -3 is a 0 = 1, the second numerator.
a 3 .a -4 is a -1, the common numerator.
After simplification: a -2 / a -1 and 1 / a -1.
4. Decrease the exponents 2a 4 / 5a 3 and 2 / a 4 and bring them to the common denominator.
Answer: 2a 3 / 5a 7 and 5a 5 / 5a 7 or 2a 3 / 5a 2 and 5 / 5a 2.
5. Multiply (a 3 + b) / b 4 by (a - b) / 3.
6. Multiply (a 5 + 1) / x 2 by (b 2 - 1) / (x + a).
7. Multiply b 4 / a -2 by h -3 / x and a n / y -3.
8. Divide a 4 / y 3 by a 3 / y 2. Answer: a / y.
Degree properties
We remind you that this lesson understands power properties with natural indicators and zero. Rational degrees and their properties will be covered in the 8th grade lessons.
A natural exponent has several important properties that make it easier to calculate in exponent examples.
Property number 1
Product of degrees
When multiplying degrees with the same bases, the base remains unchanged, and the exponents are added.
a m · a n = a m + n, where "a" is any number, and "m", "n" are any natural numbers.
This property of degrees also affects the product of three or more degrees.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
(0.8) 3 (0.8) 12 = (0.8) 3 + 12 = (0.8) 15
Please note that in the specified property it was only about the multiplication of powers with the same bases.... It does not apply to their addition.
You cannot replace the amount (3 3 + 3 2) with 3 5. This is understandable if
count (3 3 + 3 2) = (27 + 9) = 36, and 3 5 = 243
Property number 2
Private degrees
When dividing degrees with the same bases, the base remains unchanged, and the exponent of the divisor is subtracted from the exponent of the dividend.
(2b) 5: (2b) 3 = (2b) 5 - 3 = (2b) 2
11 3 - 2 4 2 - 1 = 11 4 = 44
Example. Solve the equation. We use the property of private degrees.
3 8: t = 3 4
Answer: t = 3 4 = 81
Using properties # 1 and # 2, you can easily simplify expressions and perform calculations.
- Example. Simplify the expression.
4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 - 4m - 3 = 4 2m + 5
Example. Find the value of an expression using the properties of the degree.
2 11 − 5 = 2 6 = 64
Please note that in property 2 we were talking only about dividing degrees with the same bases.
You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if we calculate (4 3 −4 2) = (64 - 16) = 48, and 4 1 = 4
Property number 3
Exponentiation
When raising a power to a power, the base of the power remains unchanged, and the exponents are multiplied.
(a n) m = a n · m, where "a" is any number, and "m", "n" are any natural numbers.

Note that property # 4, like other power properties, is applied in reverse order.
(a n b n) = (a b) n
That is, in order to multiply degrees with the same indicators, you can multiply the bases, and the exponent can be left unchanged.
2 4 5 4 = (2 5) 4 = 10 4 = 10,000
0.5 16 2 16 = (0.5 2) 16 = 1
In more complex examples, there may be cases when multiplication and division must be performed over degrees with different bases and different exponents. In this case, we advise you to proceed as follows.
For example, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
An example of raising to a decimal power.
4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4
Properties 5
Degree of quotient (fraction)
To raise a quotient to a power, you can raise a separate dividend and a divisor to this power, and divide the first result by the second.
(a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n is any natural number.
(5: 3) 12 = 5 12: 3 12
We remind you that the quotient can be represented as a fraction. Therefore, we will dwell on the topic of raising a fraction to a power in more detail on the next page.
Degrees and roots
Operations with powers and roots. Degree with negative ,
zero and fractional indicator. About expressions that don't make sense.
Operations with degrees.
1. When multiplying degrees with the same base, their indicators are added:
a m · a n = a m + n.
2. When dividing degrees with the same base, their indicators deducted .
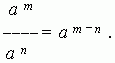
3. The degree of the product of two or more factors is equal to the product of the degrees of these factors.
4. The degree of the ratio (fraction) is equal to the ratio of the degrees of the dividend (numerator) and divisor (denominator):
(a / b) n = a n / b n.
5. When raising a degree to a degree, their indicators are multiplied:
All of the above formulas are read and executed in both directions from left to right and vice versa.
EXAMPLE (2 · 3 · 5/15) ² = 2 ² 3 ² 5 ² / 15 ² = 900/225 = 4 .
Root operations. In all the formulas below, the symbol means arithmetic root(the radical expression is positive).
1. The root of the product of several factors is equal to the product of the roots of these factors:
2. The root of the ratio is equal to the ratio of the roots of the dividend and the divisor:
![]()
3. When raising a root to a power, it is enough to raise to this power root number:

4. If we increase the degree of the root by m times and at the same time raise the radical number to the m-th power, then the value of the root will not change:
![]()
5. If we reduce the degree of the root by a factor of m and simultaneously extract the root of the m -th degree from the radical number, then the value of the root will not change:

Expansion of the concept of degree. So far, we have considered degrees only with a natural exponent; but actions with powers and roots can also lead to negative, zero and fractional indicators. All these degree indicators require additional definition.
Degree with negative exponent. The power of a number with a negative (integer) exponent is defined as a unit divided by the power of the same number with an exponent equal to the absolute value of a negative exponent:

Now the formula a m : a n = a m - n can be used not only for m greater than n, but also at m less than n .
EXAMPLE a 4: a 7 = a 4 — 7 = a — 3 .
If we want the formula a m : a n = a m — n was fair when m = n, we need a definition of the zero degree.
Zero grade. The power of any nonzero number with exponent zero is 1.
EXAMPLE 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.
Fractional exponent. In order to raise a real number a to the power of m / n, you need to extract the n-th root of the m-th power of this number a:
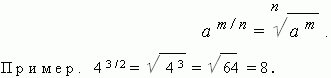
About expressions that don't make sense. There are several such expressions.
where a ≠ 0 , does not exist.
Indeed, assuming that x- some number, then in accordance with the definition of the division operation we have: a = 0· x, i.e. a= 0, which contradicts the condition: a ≠ 0
— any number.
Indeed, if we assume that this expression is equal to some number x, then, according to the definition of the division operation, we have: 0 = 0 x... But this equality holds for any number x, as required to prove.
0 0 — any number.
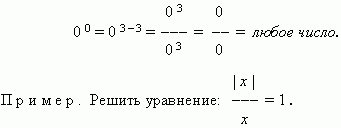
Solution. Consider three main cases:
1) x = 0 – this value does not satisfy the given equation
2) at x> 0 we get: x / x= 1, i.e. 1 = 1, whence it follows that
what x- any number; but taking into account that in
our case x> 0, the answer is x > 0 ;
Multiplication rules for powers with different radix
DEGREE WITH RATIONAL INDICATOR,
DEGREE FUNCTION IV
§ 69. Multiplication and division of degrees with the same bases
Theorem 1. To multiply degrees with the same bases, it is enough to add the exponents, and leave the base the same, that is
Proof. By definition of the degree
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
We have considered the product of two degrees. In fact, the proved property is true for any number of degrees with the same bases.
Theorem 2. To divide powers with the same bases, when the index of the dividend is greater than the index of the divisor, it is enough to subtract the index of the divisor from the index of the dividend, and leave the base the same, that is at m> n
(a =/= 0)
Proof. Recall that the quotient of dividing one number by another is a number that, when multiplied by a divisor, gives the dividend. Therefore, prove the formula where a = / = 0, this is the same as proving the formula
If m> n , then the number t - n will be natural; therefore, by Theorem 1
Theorem 2 is proved.
It should be noted that the formula
proved by us only under the assumption that m> n ... Therefore, it is not yet possible to draw from what has been proven, for example, the following conclusions:
![]()
In addition, we have not yet considered degrees with negative exponents, and we do not yet know what meaning can be given to the expression 3 - 2 .
Theorem 3. To raise a power to a power, it is enough to multiply the indicators, leaving the base of the power the same, that is
Proof. Using the definition of the degree and Theorem 1 of this section, we obtain:

Q.E.D.
For example, (2 3) 2 = 2 6 = 64;
![]()
518 (Orally.) Define NS from equations:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (U st n about.) To simplify:

520. Simplify:
521. These expressions should be presented in the form of degrees with the same bases:
1) 32 and 64; 3) 8 5 and 16 3; 5) 4 100 and 32 50;
2) -1000 and 100; 4) -27 and -243; 6) 81 75 8 200 and 3 600 4 150.
Lesson on the topic: "The rules of multiplication and division of degrees with the same and different indicators. Examples"
Additional materials
Dear users, do not forget to leave your comments, reviews, wishes. All materials have been checked by an antivirus program.
Teaching aids and simulators in the Integral online store for grade 7
Manual for the textbook Yu.N. Makarycheva Manual for the textbook A.G. Mordkovich
The purpose of the lesson: learn how to perform actions with powers of number.
To begin with, let's remember the concept of "degree of number". An expression like $ \ underbrace (a * a * \ ldots * a) _ (n) $ can be represented as $ a ^ n $.
The converse is also true: $ a ^ n = \ underbrace (a * a * \ ldots * a) _ (n) $.
This equality is called "notation of the degree as a product". It will help us determine how to multiply and divide degrees.
Remember:
a Is the base of the degree.
n- exponent.
If n = 1, therefore, the number a took once and accordingly: $ a ^ n = a $.
If n = 0, then $ a ^ 0 = 1 $.
Why this happens, we can figure out when we get acquainted with the rules of multiplication and division of powers.
Multiplication rules
a) If powers with the same base are multiplied.To $ a ^ n * a ^ m $, we write the powers as a product: $ \ underbrace (a * a * \ ldots * a) _ (n) * \ underbrace (a * a * \ ldots * a) _ (m ) $.
The figure shows that the number a have taken n + m times, then $ a ^ n * a ^ m = a ^ (n + m) $.
Example.
$2^3 * 2^2 = 2^5 = 32$.
This property is convenient to use to simplify the work when raising a number to a large power.
Example.
$2^7= 2^3 * 2^4 = 8 * 16 = 128$.
b) If the degrees are multiplied with different bases, but the same exponent.
To $ a ^ n * b ^ n $, write the degrees as a product: $ \ underbrace (a * a * \ ldots * a) _ (n) * \ underbrace (b * b * \ ldots * b) _ (m ) $.
If we swap the factors and count the resulting pairs, we get: $ \ underbrace ((a * b) * (a * b) * \ ldots * (a * b)) _ (n) $.
Hence, $ a ^ n * b ^ n = (a * b) ^ n $.
Example.
$3^2 * 2^2 = (3 * 2)^2 = 6^2= 36$.
Division rules
a) The base of the degree is the same, the indicators are different.Consider dividing an exponent with a larger exponent by dividing a exponent with a smaller exponent.
So, it is necessary $ \ frac (a ^ n) (a ^ m) $, where n> m.
Let's write the powers as a fraction:
$ \ frac (\ underbrace (a * a * \ ldots * a) _ (n)) (\ underbrace (a * a * \ ldots * a) _ (m)) $.
For convenience, we will write the division as a simple fraction.Now let's cancel the fraction.

It turns out: $ \ underbrace (a * a * \ ldots * a) _ (n-m) = a ^ (n-m) $.
Means, $ \ frac (a ^ n) (a ^ m) = a ^ (n-m) $.
This property will help explain the situation with raising a number to a zero power. Let us assume that n = m, then $ a ^ 0 = a ^ (n-n) = \ frac (a ^ n) (a ^ n) = 1 $.
Examples.
$ \ frac (3 ^ 3) (3 ^ 2) = 3 ^ (3-2) = 3 ^ 1 = 3 $.
$ \ frac (2 ^ 2) (2 ^ 2) = 2 ^ (2-2) = 2 ^ 0 = 1 $.
b) The bases of the degree are different, the indicators are the same.
Let's say you need $ \ frac (a ^ n) (b ^ n) $. Let's write the powers of numbers as a fraction:
$ \ frac (\ underbrace (a * a * \ ldots * a) _ (n)) (\ underbrace (b * b * \ ldots * b) _ (n)) $.
For convenience, let's imagine.
Using the property of fractions, we split the large fraction into the product of small ones, we get.
$ \ underbrace (\ frac (a) (b) * \ frac (a) (b) * \ ldots * \ frac (a) (b)) _ (n) $.
Accordingly: $ \ frac (a ^ n) (b ^ n) = (\ frac (a) (b)) ^ n $.
Example.
$ \ frac (4 ^ 3) (2 ^ 3) = (\ frac (4) (2)) ^ 3 = 2 ^ 3 = 8 $.
One of the main characteristics in algebra, and indeed in all mathematics, is the degree. Of course, in the 21st century, all calculations can be carried out on an online calculator, but it is better for the development of brains to learn how to do it yourself.
In this article, we will consider the most important questions regarding this definition. Namely, we will understand what it is in general and what its main functions are, what properties there are in mathematics.
Let's look at examples of how the calculation looks like, what are the basic formulas. Let's analyze the main types of quantities and how they differ from other functions.
Let's understand how to solve various problems using this value. Let's show with examples how to raise to zero power, irrational, negative, etc.
Online exponentiation calculator
What is the degree of a number
What is meant by the expression "raise a number to a power"?
The power n of the number a is the product of factors of the value a n times in a row.

Mathematically, it looks like this:
a n = a * a * a *… a n.
For example:
- 2 3 = 2 in the third step. = 2 * 2 * 2 = 8;
- 4 2 = 4 in step. two = 4 * 4 = 16;
- 5 4 = 5 in step. four = 5 * 5 * 5 * 5 = 625;
- 10 5 = 10 in 5 steps. = 10 * 10 * 10 * 10 * 10 = 100000;
- 10 4 = 10 in 4 steps. = 10 * 10 * 10 * 10 = 10000.
Below will be a table of squares and cubes from 1 to 10.
Grade table from 1 to 10
Below will be given the results of raising natural numbers to positive powers - "from 1 to 100".
| Ch-lo | 2nd article | 3rd article |
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 279 |
| 10 | 100 | 1000 |
Power properties
What is characteristic of such a mathematical function? Let's consider the basic properties.
Scientists have established the following signs characteristic of all degrees:
- a n * a m = (a) (n + m);
- a n: a m = (a) (n-m);
- (a b) m = (a) (b * m).
Let's check with examples:
2 3 * 2 2 = 8 * 4 = 32.On the other hand 2 5 = 2 * 2 * 2 * 2 * 2 = 32.
Similarly: 2 3: 2 2 = 8/4 = 2. Otherwise 2 3-2 = 2 1 = 2.
(2 3) 2 = 8 2 = 64. And if it is different? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.
As you can see, the rules work.

But what about with addition and subtraction? It's simple. First, the exponentiation is performed, and only then the addition and subtraction.
Let's see some examples:
- 3 3 + 2 4 = 27 + 16 = 43;
- 5 2 - 3 2 = 25 - 9 = 16. Please note: the rule will not work if you subtract first: (5 - 3) 2 = 2 2 = 4.
But in this case, you must first calculate the addition, since there are actions in parentheses: (5 + 3) 3 = 8 3 = 512.
How to produce calculations in more complex cases? The order is the same:
- if there are brackets - you need to start with them;
- then exponentiation;
- then perform the actions of multiplication, division;
- after addition, subtraction.
There are specific properties that are not characteristic of all degrees:
- The n-th root of the number a to the m power will be written as: a m / n.
- When raising a fraction to a power: both the numerator and its denominator are subject to this procedure.
- When raising the product of different numbers to a power, the expression will correspond to the product of these numbers to a given power. That is: (a * b) n = a n * b n.
- When raising a number to a negative step., You need to divide 1 by a number in the same st-no, but with a "+" sign.
- If the denominator of the fraction is in a negative power, then this expression will be equal to the product of the numerator and the denominator in the positive power.
- Any number in degree 0 = 1, and in step. 1 = to yourself.
These rules are important in individual cases, we will consider them in more detail below.
Degree with negative exponent
What to do when the degree is minus, i.e. when the exponent is negative?

Based on properties 4 and 5(see point above), it turns out:
A (- n) = 1 / A n, 5 (-2) = 1/5 2 = 1/25.
And vice versa:
1 / A (- n) = A n, 1/2 (-3) = 2 3 = 8.
And if a fraction?
(A / B) (- n) = (B / A) n, (3/5) (-2) = (5/3) 2 = 25/9.
Degree with natural exponent
It is understood as a degree with indicators equal to whole numbers.
Things to remember:
A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1 ... etc.
A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3 ... etc.
In addition, if (-a) 2 n +2, n = 0, 1, 2 ... then the result will be with a "+" sign. If a negative number is raised to an odd power, then vice versa.
General properties, and all the specific features described above, are also characteristic of them.
Fractional degree
This view can be written by the scheme: A m / n. It reads as: n-th root of the number A to the m power.

You can do whatever you want with a fractional exponent: reduce it, decompose it into parts, raise it to a different degree, etc.
Irrational grade
Let α be an irrational number and A ˃ 0.
To understand the essence of a degree with such an indicator, consider different possible cases:
- A = 1. The result will be equal to 1. Since there is an axiom - 1 in all degrees is equal to one;
А r 1 ˂ А α ˂ А r 2, r 1 ˂ r 2 - rational numbers;
- 0˂А˂1.
In this case, on the contrary: А r 2 ˂ А α ˂ А r 1 under the same conditions as in the second paragraph.
For example, the exponent is π. It is rational.
r 1 - in this case is equal to 3;
r 2 - will be equal to 4.
Then, for A = 1, 1 π = 1.
A = 2, then 2 3 ˂ 2 π ˂ 2 4, 8 ˂ 2 π ˂ 16.
А = 1/2, then (½) 4 ˂ (½) π ˂ (½) 3, 1/16 ˂ (½) π ˂ 1/8.
These degrees are characterized by all the mathematical operations and specific properties described above.
Conclusion
To summarize - what are these values for, what is the advantage of such functions? Of course, first of all, they simplify the life of mathematicians and programmers when solving examples, since they allow you to minimize calculations, shorten algorithms, organize data, and much more.
Where else can this knowledge be useful? In any working specialty: medicine, pharmacology, dentistry, construction, engineering, engineering, design, etc.
If you need to raise a specific number to a power, you can use. And now we will dwell in more detail on properties of degrees.
Exponential numbers open up great possibilities, they allow us to transform multiplication into addition, and adding is much easier than multiplying.
For example, we need to multiply 16 by 64. The product of the multiplication of these two numbers is 1024. But 16 is 4x4, and 64 is 4x4x4. That is, 16 by 64 = 4x4x4x4x4, which is also 1024.
The number 16 can also be represented as 2x2x2x2, and 64 as 2x2x2x2x2x2, and if we multiply, we again get 1024.
Now let's use the rule. 16 = 4 2, or 2 4, 64 = 4 3, or 2 6, at the same time 1024 = 6 4 = 4 5, or 2 10.
Therefore, our problem can be written differently: 4 2 x4 3 = 4 5 or 2 4 x2 6 = 2 10, and each time we get 1024.
We can solve a number of similar examples and see that multiplying numbers with powers reduces to addition of exponents, or exponential, of course, provided that the bases of the factors are equal.
Thus, without multiplying, we can immediately say that 2 4 x2 2 x2 14 = 2 20.
This rule is also true when dividing numbers with powers, but in this case, e the exponent of the divisor is subtracted from the exponent of the dividend... Thus, 2 5: 2 3 = 2 2, which in ordinary numbers is 32: 8 = 4, that is, 2 2. Let's summarize:
a m х a n = a m + n, a m: a n = a m-n, where m and n are integers.
At first glance, it may seem what is multiplication and division of numbers with powers not very convenient, because first you need to represent the number in exponential form. It is not difficult to represent the numbers 8 and 16 in this form, that is, 2 3 and 2 4, but how to do this with the numbers 7 and 17? Or what to do when the number can be represented in exponential form, but the bases of the exponential expressions of numbers are very different. For example, 8 × 9 is 2 3 × 3 2, in which case we cannot sum the exponents. Neither 2 5 nor 3 5 is the answer, nor does the answer lie in the interval between these two numbers.
Then is it worth bothering with this method at all? Definitely worth it. It offers tremendous benefits, especially for complex and time consuming computations.
Popular:
New
- SIT30 Body Building Systems Principles - The Real Story of Your Transformation
- Sit30 application - ideal body system - "The best application for me" Training program for body types: what, why and why
- Ideal body workshop SIT30 global healing system for the whole body - a real story of your transformation
- Goal Setting Course "Don't Delay!
- In what areas is goal setting applied?
- Goal setting - technology and process
- Innovative school of coaching Dovlatov training
- Real review about the school of drawing by veronika kalacheva school of painting by veronika kalacheva
- Balancing Feedback
- Greetings in Japanese: different options How to speak Japanese






