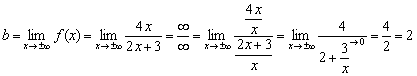Fonksiyon Çizimi AsimptotlarıAsimptotun hayaleti, nihayet ayrı bir makalede somutlaşmak ve şaşkın okuyucuları memnun etmek için siteyi uzun süredir dolaşıyor. fonksiyonun tam keşfi... Grafiğin asimptotlarını bulmak, olaylar hesaplama etrafında döndüğünden, okul kursunda yalnızca genel bir sırayla ele alınan belirtilen görevin birkaç bölümünden biridir. fonksiyonların sınırları, ama yine de yüksek matematiğe aittirler. Matematiksel analiz konusunda yetersiz bilgili ziyaretçiler, bence ipucu açık ;-) ... dur-dur, nereye gidiyorsun? limitler- bu kolay! Asimptot örnekleri ile ilgili ilk derste hemen karşılaşıldı. temel fonksiyonların grafikleri, ve şimdi konu ayrıntılı olarak değerlendiriliyor.
Peki asimptot nedir?
Düşünmek değişken nokta, işlevin programına göre "sürüyor". asimptot Düz, ne için sınırsız yakın Bir fonksiyonun grafiği, değişken noktasını sonsuza taşırken yaklaşır.
Not
: gösterimde bir formülasyona ihtiyacınız varsa tanım anlamlıdır matematiksel analiz lütfen öğreticiye bakın.
Düzlemde asimptotlar doğal konumlarına göre sınıflandırılır:
1) Dikey asimtotlar"alfa"nın gerçek bir sayı olduğu formun bir denklemi ile verilen . Popüler temsilci, y ekseninin kendisini tanımlar,
hafif bir mide bulantısı ile abartmayı hatırlıyoruz.
2) eğik asimptotlar geleneksel olarak kaydedilmiş doğrunun denklemi bir eğim ile. Bazen özel bir durum ayrı bir grup olarak seçilir - yatay asimptotlar... Örneğin, asimptotlu aynı hiperbol.
Hızlıca gidiyoruz, kısa bir otomatik silah patlaması ile konuya girelim:
Bir fonksiyon grafiğinin kaç asimptotu olabilir?
Hiçbiri, bir, iki, üç, ... veya sonsuz sayıda. Örnekler için uzağa gitmeyeceğiz, unutmayın temel fonksiyonlar... Parabol, kübik parabol, sinüzoidin hiç asimptotu yoktur. Üstel, logaritmik bir fonksiyonun grafiğinin tek bir asimptotu vardır. Ark tanjant ve ark kotanjantında iki tane vardır ve tanjant ve kotanjant sonsuz sayıdadır. Bir grafiğin hem yatay hem de dikey asimptotlarla tamamlanması nadir değildir. Abartma, seni her zaman sevecek.
Ne demek ?
Bir Fonksiyon Grafiğinin Dikey Asimptotları
Grafiğin dikey asimptotu genellikle bulunur sonsuz kırılma noktasında fonksiyonlar. Çok basit: eğer bir fonksiyon bir noktada sonsuz süreksizliğe maruz kalıyorsa, o zaman denklem tarafından verilen düz çizgi grafiğin dikey asimptotu olur.
Not
: Notasyonun tamamen farklı iki kavramı belirtmek için kullanıldığını unutmayın. Nokta ima edilir veya düz çizginin denklemi - bağlama bağlıdır.
Böylece, bir noktada bir düşey asimptotun varlığını saptamak için şunu göstermek yeterlidir: en az bir tek taraflı sınırlardan  sonsuz. Çoğu zaman bu, fonksiyonun paydasının sıfır olduğu noktadır. Hal böyle olunca dersin son örneklerinde dikey asimptotları zaten bulduk. fonksiyonun sürekliliği hakkında... Ancak bazı durumlarda yalnızca tek taraflı bir sınır vardır ve eğer sonsuz ise, o zaman tekrar - dikey asimptotu sevin ve tercih edin. En basit örnek: ve ordinat ekseni (bkz. Temel fonksiyonların grafikleri ve özellikleri). sonsuz. Çoğu zaman bu, fonksiyonun paydasının sıfır olduğu noktadır. Hal böyle olunca dersin son örneklerinde dikey asimptotları zaten bulduk. fonksiyonun sürekliliği hakkında... Ancak bazı durumlarda yalnızca tek taraflı bir sınır vardır ve eğer sonsuz ise, o zaman tekrar - dikey asimptotu sevin ve tercih edin. En basit örnek: ve ordinat ekseni (bkz. Temel fonksiyonların grafikleri ve özellikleri).
Açık gerçek, yukarıdakilerden de kaynaklanmaktadır: fonksiyon sürekli ise, o zaman dikey asimptot yok... Nedense aklıma bir parabol geldi. Gerçekten de, burada düz bir çizgiyi nereye "yapıştırabilirsiniz"? ... evet ... anlıyorum ... Freud Amca'nın takipçileri histerikti =) Converse ifadesi genellikle doğru değildir: örneğin, fonksiyon tüm sayı doğrusunda tanımlanmamıştır, ancak asimptotlardan tamamen yoksundur.
Bir fonksiyonun grafiğinin eğimli asimptotları
Eğik (özel bir durum olarak - yatay) asimptotlar, işlev argümanı "artı sonsuz" veya "eksi sonsuz" olma eğilimindeyse çizilebilir. Bu yüzden bir fonksiyonun grafiği ikiden fazla eğik asimptot içeremez... Örneğin, üstel bir fonksiyonun grafiğinde tek bir yatay asimptot bulunur ve noktasında arktanjantın grafiğinde bu tür iki asimptot ve farklı asimptot bulunur.
Buradaki grafik tek eğik asimptota yaklaştığında, "sonsuzluğu" tek bir notasyon altında birleştirmek gelenekseldir. Örneğin, ... doğru tahmin ettiniz:.
Genel kural:
iki tane varsa son sınır  , o zaman düz çizgi, fonksiyonun grafiğinin eğik asimptotudur. Eğer en az bir listelenen sınırların sonsuz olması durumunda eğik asimptot yoktur. , o zaman düz çizgi, fonksiyonun grafiğinin eğik asimptotudur. Eğer en az bir listelenen sınırların sonsuz olması durumunda eğik asimptot yoktur.
Not
: "x" yalnızca "artı sonsuz" veya yalnızca "eksi sonsuz" eğilimindeyse formüller geçerli kalır.
Parabolün eğik asimptotu olmadığını gösterelim:

Limit sonsuzdur, yani eğik asimptot yoktur. Sınırı bulmada şunu unutmayın:  cevap zaten alındığı için artık gerekli değil. cevap zaten alındığı için artık gerekli değil.
Not
: "artı-eksi", "eksi-artı" işaretlerini anlamakta zorluk çekiyorsanız (veya yaşayacaksanız), lütfen dersin başındaki yardıma bakın.
sonsuz küçük fonksiyonlarda, size bu işaretleri nasıl doğru yorumlayacağınızı söyledim.
Açıkçası, herhangi bir ikinci dereceden, kübik fonksiyon, 4. ve daha yüksek derecelerin polinomu da eğik asimptotlara sahip değildir.
Şimdi grafik için eğik asimptot olmadığından emin olalım. Belirsizliği ifşa etmek için kullanırız L'Hôpital kuralı:
, doğrulanması gerekiyordu.
İşlev süresiz olarak büyüdüğünde, ancak grafiğinin yaklaşacağı düz bir çizgi olmadığında sonsuz yakın.
Dersin pratik kısmına geçelim:
Bir fonksiyonun grafiğinin asimptotları nasıl bulunur?
Bu şekilde formüle edilir tipik görev ve grafiğin TÜM asimptotlarını (dikey, eğik / yatay) bulmayı varsayar. Sorunun formülasyonunda daha kesin olmak gerekirse, asimptotların varlığına yönelik bir çalışmadan bahsediyoruz (sonuçta böyle olmayabilir). Basit bir şeyle başlayalım:
örnek 1
Bir fonksiyonun grafiğinin asimptotlarını bulun
Çözüm iki noktaya bölmek uygundur:
1) İlk önce dikey asimptot olup olmadığını kontrol ediyoruz. Payda noktasında kaybolur ve belirli bir noktada fonksiyonun zarar gördüğü hemen anlaşılır. sonsuz mola, ve denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin dikey asimptotudur. Ancak, böyle bir sonuca varmadan önce, tek taraflı sınırlar bulmak gerekir:

Makalede benzer şekilde üzerinde durduğum hesaplama tekniğini hatırlatıyorum. Fonksiyonun sürekliliği. kırılma noktaları... İfadede "x" yerine limit işaretinin altında yer değiştiririz. Payda ilginç bir şey yok:
.
Ama paydada çıkıyor sonsuz küçük negatif sayı:
, aynı zamanda sınırın kaderini de belirler.
Sol taraflı limit sonsuzdur ve prensipte dikey bir asimptotun varlığı hakkında bir karara varmak zaten mümkündür. Ancak tek taraflı sınırlar sadece bunun için gerekli değildir - ANLAMAYA YARDIMCI OLUR, NASIL fonksiyon grafiği bulunur ve çizilir DOĞRU ŞEKİLDE... Bu nedenle, sağ limiti de hesaplamalıyız:

Çıktı: tek taraflı limitler sonsuzdur; bu, doğrunun, fonksiyonun grafiğinin dikey asimptotu olduğu anlamına gelir.
İlk sınır sonlu, bu da "konuşmaya devam etmek" ve ikinci sınırı bulmak gerektiği anlamına gelir:
İkinci sınır da sonlu.
Yani asimptotumuz:
Çıktı: denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Yatay asimptotu bulmak için
basitleştirilmiş bir formül kullanabilirsiniz:
Varsa sonlu limit, o zaman düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Fonksiyonun pay ve paydasının olduğunu görmek kolaydır. aynı büyüme düzeni, bu, istenen sınırın sonlu olacağı anlamına gelir:
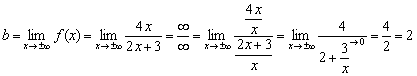
Cevap:
Koşul olarak, çizimi tamamlamanız gerekmez, ancak tüm hızıyla devam ediyorsa fonksiyon çalışması, sonra taslakta hemen çizeriz:

Bulunan üç limite dayanarak, fonksiyonun grafiğinin nasıl bulunabileceğini kendiniz bulmaya çalışın. Gerçekten zor mu? 5-6-7-8 puan bulun ve çizim üzerinde işaretleyin. Ancak, bu fonksiyonun grafiği kullanılarak oluşturulmuştur. temel bir fonksiyonun grafiğinin dönüşümleri, ve bu makalenin 21. Örneği'ni dikkatlice inceleyen okuyucular bu eğrinin ne olduğunu kolayca tahmin edeceklerdir.
Örnek 2
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bu, kendin yap çözümüne bir örnektir. Sürecin uygun bir şekilde iki noktaya bölünebileceğini hatırlatmama izin verin - dikey asimptotlar ve eğik asimptotlar. Örnek çözümde Yatay asimptot basitleştirilmiş bir şema ile bulunur.
Uygulamada, kesirli-rasyonel fonksiyonlara en sık rastlanır ve hiperboller üzerine eğitimden sonra görevi zorlaştıracağız:
Örnek 3
Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: Bir, iki ve bitti:
1) Dikey asimptotlar bulunur sonsuz süreksizlik noktalarında, bu yüzden paydanın kaybolup kaybolmadığını kontrol etmeniz gerekir. çözeceğiz ikinci dereceden denklem:

Diskriminant pozitiftir, bu nedenle denklemin iki gerçek kökü vardır ve iş önemli ölçüde eklenir =)

Tek taraflı limitleri daha fazla bulmak için, kare üç terimliyi çarpanlara ayırmak uygundur.:
(Kompakt gösterim için, ilk parantez içine "eksi" konuldu). Güvenli tarafta olmak için, parantezleri açarak zihinsel veya taslak üzerinde bir kontrol yapacağız.
Fonksiyonu şu şekilde yeniden yazıyoruz 
Bir noktada tek taraflı limitleri bulalım:

Ve noktada:

Bu nedenle, düz çizgiler, incelenen fonksiyonun grafiğinin dikey asimptotlarıdır.
2) fonksiyona bakmak 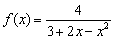 , o zaman limitin sonlu olacağı ve yatay bir asimptotumuz olduğu oldukça açıktır. Varlığını kısaca gösterelim: , o zaman limitin sonlu olacağı ve yatay bir asimptotumuz olduğu oldukça açıktır. Varlığını kısaca gösterelim:

Böylece düz çizgi (apsis ekseni) bu fonksiyonun grafiğinin yatay asimptotu olur.
Cevap:
Bulunan limitler ve asimptotlar, fonksiyonun grafiği hakkında birçok bilgi sağlar. Aşağıdaki gerçekleri dikkate alarak çizimi görselleştirmeye çalışın:

Grafiğin versiyonunu bir taslak üzerinde çizin.
Elbette, bulunan limitler grafiğin türünü kesin olarak belirlemez ve bir hata yapabilirsiniz, ancak alıştırmanın kendisi kursta paha biçilmez yardım sağlayacaktır. tam fonksiyon çalışması... Doğru resim dersin sonundadır.
Örnek 4
Bir fonksiyonun grafiğinin asimptotlarını bulun
Örnek 5
Bir fonksiyonun grafiğinin asimptotlarını bulun
 Bunlar bağımsız bir çözüm için görevlerdir. Her iki grafik de yine aşağıdaki özellikler tarafından hemen tespit edilen yatay asimptotlara sahiptir: Örnek 4'te büyüme sırası payda daha fazla payın büyüme sırasından daha fazladır ve Örnek 5'te pay ve payda aynı büyüme düzeni... Örnek çözümde, birinci fonksiyon tam bir şekilde eğik asimptotların varlığı için ve ikincisi - sınır boyunca araştırılır.
Benim öznel izlenimime göre yatay asimptotlar, "gerçekten eğik" olanlardan belirgin şekilde daha yaygındır. Uzun zamandır beklenen genel dava:
Örnek 6
Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: türün klasikleri:
1) Payda pozitif olduğu için fonksiyon sürekli tam sayı doğrusunda ve dikey asimptot yok. …İyi mi? Yanlış kelime - harika! 1 numaralı nokta kapalı.
2) Eğik asimptotların varlığını kontrol edin:
İlk sınır sonlu, bu yüzden daha ileri gidiyoruz. Ortadan kaldırmak için ikinci limiti hesaplarken belirsizlikler "sonsuz eksi sonsuz" ifadesini getiriyoruz ortak payda:

İkinci sınır da sonlu, bu nedenle, söz konusu fonksiyonun grafiği eğik bir asimptota sahiptir:
Çıktı:
Böylece, fonksiyonun grafiği  sonsuz yakın düz çizgiye yaklaşır: sonsuz yakın düz çizgiye yaklaşır:

Eğik asimptotunu orijinde geçtiğini ve bu tür kesişme noktalarının oldukça kabul edilebilir olduğunu unutmayın - sonsuzda "her şeyin normal olması" önemlidir (aslında, asimptotlarla ilgili konuşma tam oraya gelir).
Örnek 7
Bir fonksiyonun grafiğinin asimptotlarını bulun
Çözüm: Yorumlanacak özel bir şey yok, bu yüzden temiz bir çözümün yaklaşık bir örneğini çizeceğim:
1) Dikey asimptotlar. Noktayı inceleyin.

Düz çizgi, 'deki grafiğin dikey asimptotudur.
2) Eğik asimptotlar:

Düz çizgi, grafiği için eğik bir asimptottur.
Cevap: 
Bulunan tek taraflı limitler ve yüksek güvenilirliğe sahip asimptotlar, bu fonksiyonun grafiğinin nasıl göründüğünü varsaymamızı sağlar. Dersin sonunda doğru çizim.
Örnek 8
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bu, bağımsız bir çözüm için bir örnektir, bazı limitleri hesaplamanın rahatlığı için, payı paydaya göre terime bölebilirsiniz. Ve yine, elde edilen sonuçları analiz ederek, bu fonksiyonun bir grafiğini çizmeye çalışın.
Açıktır ki, "gerçek" eğik asimptotların sahipleri, payın en yüksek derecesi olan kesirli rasyonel fonksiyonların grafikleridir. bir tane daha paydanın en yüksek derecesi. Daha büyükse, eğik asimptot artık mevcut olmayacaktır (örneğin,).
Ama hayatta başka mucizeler de olur:
Örnek 9
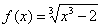
Örnek 11
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin
Çözüm: belli ki  , bu nedenle, sadece fonksiyonun grafiğinin olduğu sağ yarım düzlemi dikkate alıyoruz. , bu nedenle, sadece fonksiyonun grafiğinin olduğu sağ yarım düzlemi dikkate alıyoruz.
Böylece, düz çizgi (ordinat ekseni), fonksiyonun grafiği için dikey asimptottur.
2) Eğik asimptot çalışması tam şemaya göre yapılabilir, ancak makalede L'Hôpital'in kuralları bunu öğrendik doğrusal fonksiyon daha fazla yüksek mertebe logaritmik büyüme, bu nedenle: 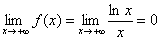 (aynı dersten Örnek 1'e bakın). (aynı dersten Örnek 1'e bakın).
Sonuç: apsis ekseni, fonksiyonun grafiğinin yatay asimptotudur.
Cevap:
, Eğer ;
, Eğer .
Netlik için çizim:

Görünüşte benzer bir fonksiyonun hiçbir asimptotu olmaması ilginçtir (isteyenler bunu kontrol edebilir).
Son iki kendi kendine çalışma örneği:
Örnek 12
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin
 |
Çözümü iki noktaya bölmek uygundur:
1) İlk önce dikey asimptot olup olmadığını kontrol ediyoruz. Paydada yok olur ve belirli bir noktada fonksiyonun sonsuz bir süreksizliğe maruz kaldığı ve denklem tarafından verilen düz çizginin fonksiyon grafiğinin dikey asimptotu olduğu hemen anlaşılır. Ancak, böyle bir sonuca varmadan önce, tek taraflı sınırlar bulmak gerekir:

Bir fonksiyonun sürekliliği makalesinde benzer şekilde üzerinde durduğum hesaplama tekniğini size hatırlatıyorum. Kırılma noktaları. İfadede "x" yerine limit işaretinin altında yer değiştiririz. Payda ilginç bir şey yok:
Ancak paydada sonsuz küçük bir negatif sayı elde edilir:
Sınırın kaderini belirler.
Sol taraflı limit sonsuzdur ve prensipte dikey bir asimptotun varlığı hakkında bir karara varmak zaten mümkündür. Ancak tek taraflı limitler sadece bunun için gerekli değildir - bunlar fonksiyon grafiğinin NASIL yerleştirildiğini ANLAMAYA ve DOĞRU YAPILMASINA YARDIMCI OLUR. Bu nedenle, sağ limiti de hesaplamalıyız:

Sonuç: tek taraflı limitler sonsuzdur, bu, düz çizginin, fonksiyonun grafiğinin dikey asimptotu olduğu anlamına gelir.
İlk sınır sonludur, yani "konuşmaya devam etmek" ve ikinci sınırı bulmak gerekir:
İkinci sınır da sonludur.
Yani asimptotumuz:
Sonuç: denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Yatay asimptotu bulmak için basitleştirilmiş bir formül kullanabilirsiniz:
Sonlu bir limit varsa, o zaman düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Fonksiyonun pay ve paydasının aynı büyüme düzeninde olduğunu görmek kolaydır, bu da istenen limitin sonlu olacağı anlamına gelir:

Duruma göre, çizimi tamamlamanız gerekmez, ancak işlevin çalışması tüm hızıyla devam ediyorsa, taslakta hemen bir eskiz yaparız:

Bulunan üç limite dayanarak, fonksiyon grafiğinin nasıl bulunabileceğini kendiniz bulmaya çalışın. Gerçekten zor mu? 5-6-7-8 puan bulun ve çizim üzerinde işaretleyin. Ancak, bu fonksiyonun grafiği, grafik dönüşümleri kullanılarak oluşturulmuştur. temel fonksiyon, ve bu makalenin 21. Örneği'ni dikkatlice inceleyen okuyucular bu eğrinin ne olduğunu kolayca tahmin edeceklerdir.
Bu, kendin yap çözümüne bir örnektir. Sürecin uygun bir şekilde iki noktaya bölünebileceğini hatırlatmama izin verin - dikey asimptotlar ve eğik asimptotlar. Örnek çözümde, basitleştirilmiş bir şema kullanılarak yatay asimptot bulunur.
Uygulamada, kesirli-rasyonel fonksiyonlara en sık rastlanır ve hiperboller üzerine eğitimden sonra görevi zorlaştıracağız:
Bir fonksiyonun grafiğinin asimptotlarını bulun
Çözüm: Bir, iki ve bitti:
1) Dikey asimptotlar sonsuz süreksizlik noktalarındadır, bu nedenle paydanın kaybolup kaybolmadığını kontrol etmeniz gerekir. çözeceğiz ikinci dereceden denklem:

Diskriminant pozitiftir, bu nedenle denklemin iki gerçek kökü vardır ve iş önemli ölçüde eklenir

Tek taraflı limitleri daha fazla bulmak için kare üç terimliyi çarpanlara ayırmak uygundur:
(Kompakt gösterim için, ilk parantez içine "eksi" konuldu). Güvenli tarafta olmak için, parantezleri açarak zihinsel veya taslak üzerinde bir kontrol yapacağız.
Fonksiyonu şu şekilde yeniden yazıyoruz

Bir noktada tek taraflı limitleri bulalım:

asimptot grafiği fonksiyon limiti
Ve noktada:

Bu nedenle, düz çizgiler, incelenen fonksiyonun grafiğinin dikey asimptotlarıdır.
2) Fonksiyona bakarsanız, limitin sonlu olacağı ve yatay bir asimptotumuz olduğu oldukça açıktır. Varlığını kısaca gösterelim:


Böylece düz çizgi (apsis ekseni) bu fonksiyonun grafiğinin yatay asimptotu olur.
Bulunan limitler ve asimptotlar, fonksiyonun grafiği hakkında birçok bilgi sağlar. Aşağıdaki gerçekleri dikkate alarak çizimi görselleştirmeye çalışın:

Grafiğin versiyonunu bir taslak üzerinde çizin.
Elbette, bulunan limitler grafiğin türünü açık bir şekilde belirlemez ve bir hata yapabilirsiniz, ancak fonksiyonun eksiksiz bir incelemesi sırasında alıştırmanın kendisi çok değerli olacaktır. Doğru resim dersin sonundadır.
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bir fonksiyonun grafiğinin asimptotlarını bulun

Bunlar bağımsız bir çözüm için görevlerdir. Her iki grafik de yine aşağıdaki işaretlerle hemen tespit edilen yatay asimptotlara sahiptir: Örnek 4'te, paydanın büyüme sırası, payın büyüme sırasından büyüktür ve Örnek 5'te, pay ve payda, aynı büyüme düzeni. Örnek çözümde, birinci fonksiyon tam bir şekilde eğik asimptotların varlığı için ve ikincisi - sınır boyunca araştırılır.
Benim öznel izlenimime göre yatay asimptotlar, "gerçekten eğik" olanlardan belirgin şekilde daha yaygındır. Uzun zamandır beklenen genel dava:
Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: türün klasikleri:
- 1) Payda pozitif olduğu için fonksiyon tam sayı doğrusunda süreklidir ve dikey asimptot yoktur. …İyi mi? Yanlış kelime - harika! 1 numaralı nokta kapalı.
- 2) Eğik asimptotların varlığını kontrol edin:

İkinci sınır da sonludur, bu nedenle, söz konusu fonksiyonun grafiği eğik bir asimptota sahiptir:
Böylece, fonksiyonun grafiği düz bir çizgiye sonsuz derecede yakındır.
Eğik asimptotunu orijinde geçtiğini ve bu tür kesişme noktalarının oldukça kabul edilebilir olduğunu unutmayın - sonsuzda "her şeyin normal olması" önemlidir (aslında, asimptotlarla ilgili konuşma tam oraya gelir).

Bir fonksiyonun grafiğinin asimptotlarını bulun
Çözüm: Yorumlanacak özel bir şey yok, bu yüzden temiz bir çözümün yaklaşık bir örneğini çizeceğim:
1) Dikey asimptotlar. Noktayı inceleyin.

Düz çizgi, 'deki grafiğin dikey asimptotudur.
2) Eğik asimptotlar:

Düz çizgi, grafiği için eğik bir asimptottur.
Bulunan tek taraflı limitler ve yüksek güvenilirliğe sahip asimptotlar, bu fonksiyonun grafiğinin nasıl göründüğünü varsaymamızı sağlar.
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bu, bağımsız bir çözüm için bir örnektir, bazı limitleri hesaplamanın rahatlığı için, payı paydaya göre terime bölebilirsiniz. Ve yine, elde edilen sonuçları analiz ederek, bu fonksiyonun bir grafiğini çizmeye çalışın.
Açıktır ki, "gerçek" eğik asimptotların sahipleri, payın en yüksek derecesinin paydanın en yüksek derecesinden bir fazla olduğu kesirli-rasyonel fonksiyonların grafikleridir. Daha büyükse, eğik asimptot artık mevcut olmayacaktır (örneğin,).
Ama hayatta başka mucizeler de olur.
Tipik bir görev bu şekilde formüle edilir ve grafiğin TÜM asimptotlarını (dikey, eğik / yatay) bulmayı içerir. Sorunun formülasyonunda daha kesin olmak gerekirse, asimptotların varlığına yönelik bir çalışmadan bahsediyoruz (sonuçta böyle olmayabilir).
Basit bir şeyle başlayalım:
örnek 1
Çözüm iki noktaya bölmek uygundur:
1) İlk önce dikey asimptot olup olmadığını kontrol ediyoruz. Payda noktasında kaybolur ve belirli bir noktada fonksiyonun zarar gördüğü hemen anlaşılır. sonsuz mola, ve denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin dikey asimptotudur. Ancak, böyle bir sonuca varmadan önce, tek taraflı sınırlar bulmak gerekir:

Makalede benzer şekilde üzerinde durduğum hesaplama tekniğini hatırlatıyorum. fonksiyonun sürekliliği. kırılma noktaları... İfadede "x" yerine limit işaretinin altında yer değiştiririz. Payda ilginç bir şey yok:
.
Ama paydada çıkıyor sonsuz küçük negatif sayı:
, aynı zamanda sınırın kaderini de belirler.
Sol taraflı limit sonsuzdur ve prensipte dikey bir asimptotun varlığı hakkında bir karara varmak zaten mümkündür. Ancak tek taraflı sınırlar sadece bunun için gerekli değildir - ANLAMAYA YARDIMCI OLUR, NASIL fonksiyon grafiği bulunur ve çizilir DOĞRU ŞEKİLDE... Bu nedenle, sağ limiti de hesaplamalıyız:

Çıktı: tek taraflı limitler sonsuzdur; bu, doğrunun, fonksiyonun grafiğinin dikey asimptotu olduğu anlamına gelir.
İlk sınır sonlu, bu da "konuşmaya devam etmek" ve ikinci sınırı bulmak gerektiği anlamına gelir:
İkinci sınır da sonlu.
Yani asimptotumuz:
Çıktı: denklem tarafından verilen düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Yatay asimptotu bulmak için basitleştirilmiş bir formül kullanabilirsiniz:
Sonlu bir limit varsa, o zaman düz çizgi, fonksiyonun grafiğinin yatay asimptotudur.
Fonksiyonun pay ve paydasının olduğunu görmek kolaydır. aynı büyüme düzeni, bu, istenen sınırın sonlu olacağı anlamına gelir:

Cevap:
Koşul olarak, çizimi tamamlamanız gerekmez, ancak tüm hızıyla devam ediyorsa fonksiyon çalışması, sonra taslakta hemen çizeriz:

Bulunan üç limite dayanarak, fonksiyonun grafiğinin nasıl bulunabileceğini kendiniz bulmaya çalışın. Gerçekten zor mu? 5-6-7-8 puan bulun ve çizim üzerinde işaretleyin. Ancak, bu fonksiyonun grafiği kullanılarak oluşturulmuştur. temel bir fonksiyonun grafiğinin dönüşümleri, ve bu makalenin 21. Örneği'ni dikkatlice inceleyen okuyucular bu eğrinin ne olduğunu kolayca tahmin edeceklerdir.
Örnek 2
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bu, kendin yap çözümüne bir örnektir. Sürecin uygun bir şekilde iki noktaya bölünebileceğini hatırlatmama izin verin - dikey asimptotlar ve eğik asimptotlar. Örnek çözümde, basitleştirilmiş bir şema kullanılarak yatay asimptot bulunur.
Uygulamada, kesirli-rasyonel fonksiyonlara en sık rastlanır ve hiperboller üzerine eğitimden sonra görevi zorlaştıracağız:
Örnek 3
Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: Bir, iki ve bitti:
1) Dikey asimptotlar bulunur sonsuz süreksizlik noktalarında, bu yüzden paydanın kaybolup kaybolmadığını kontrol etmeniz gerekir. çözeceğiz ikinci dereceden denklem :

Diskriminant pozitiftir, bu nedenle denklemin iki gerçek kökü vardır ve iş önemli ölçüde eklenir =)

Tek taraflı limitleri daha fazla bulmak için, kare üç terimliyi çarpanlara ayırmak uygundur.:
(Kompakt gösterim için, ilk parantez içine "eksi" konuldu). Güvenli tarafta olmak için, parantezleri açarak zihinsel veya taslak üzerinde bir kontrol yapacağız.
Fonksiyonu şu şekilde yeniden yazıyoruz 
Bir noktada tek taraflı limitleri bulalım:

Ve noktada:

Bu nedenle, düz çizgiler, incelenen fonksiyonun grafiğinin dikey asimptotlarıdır.
2) fonksiyona bakmak  , o zaman limitin sonlu olacağı ve yatay bir asimptotumuz olduğu oldukça açıktır. Varlığını kısaca gösterelim:
, o zaman limitin sonlu olacağı ve yatay bir asimptotumuz olduğu oldukça açıktır. Varlığını kısaca gösterelim:

Böylece düz çizgi (apsis ekseni) bu fonksiyonun grafiğinin yatay asimptotu olur.
Cevap:
Bulunan limitler ve asimptotlar, fonksiyonun grafiği hakkında birçok bilgi sağlar. Aşağıdaki gerçekleri dikkate alarak çizimi görselleştirmeye çalışın:

Grafiğin versiyonunu bir taslak üzerinde çizin.
Elbette, bulunan limitler grafiğin türünü kesin olarak belirlemez ve bir hata yapabilirsiniz, ancak alıştırmanın kendisi kursta paha biçilmez yardım sağlayacaktır. tam fonksiyon çalışması... Doğru resim dersin sonundadır.
Örnek 4
Bir fonksiyonun grafiğinin asimptotlarını bulun
Örnek 5
Bir fonksiyonun grafiğinin asimptotlarını bulun

Bunlar bağımsız bir çözüm için görevlerdir. Her iki grafik de yine aşağıdaki özellikler tarafından hemen tespit edilen yatay asimptotlara sahiptir: Örnek 4'te büyüme sırası payda payın büyüme sırasından büyüktür ve Örnek 5'te pay ve payda aynı büyüme düzeni... Örnek çözümde, birinci fonksiyon tam bir şekilde eğik asimptotların varlığı için ve ikincisi - sınır boyunca araştırılır.
Benim öznel izlenimime göre yatay asimptotlar, "gerçekten eğik" olanlardan belirgin şekilde daha yaygındır. Uzun zamandır beklenen genel dava:
Örnek 6
Bir fonksiyonun grafiğinin asimptotlarını bulun

Çözüm: türün klasikleri:
1) Payda pozitif olduğu için fonksiyon sürekli tam sayı doğrusunda ve dikey asimptot yok. …İyi mi? Yanlış kelime - harika! 1 numaralı nokta kapalı.
2) Eğik asimptotların varlığını kontrol edin:
İlk sınır sonlu, bu yüzden daha ileri gidiyoruz. Ortadan kaldırmak için ikinci limiti hesaplarken belirsizlikler "sonsuz eksi sonsuz" ifadeyi ortak bir paydaya getiriyoruz:

İkinci sınır da sonlu, bu nedenle, söz konusu fonksiyonun grafiği eğik bir asimptota sahiptir:
Çıktı:
Böylece, fonksiyonun grafiği  sonsuz yakın düz çizgiye yaklaşır:
sonsuz yakın düz çizgiye yaklaşır:

Eğik asimptotunu orijinde geçtiğini ve bu tür kesişme noktalarının oldukça kabul edilebilir olduğunu unutmayın - sonsuzda "her şeyin normal olması" önemlidir (aslında, asimptotlarla ilgili konuşma tam oraya gelir).
Örnek 7
Bir fonksiyonun grafiğinin asimptotlarını bulun
Çözüm: Yorumlanacak özel bir şey yok, bu yüzden temiz bir çözümün yaklaşık bir örneğini çizeceğim:
1) Dikey asimptotlar. Noktayı inceleyin.

Düz çizgi, 'deki grafiğin dikey asimptotudur.
2) Eğik asimptotlar:

Düz çizgi, grafiği için eğik bir asimptottur.
Cevap: 
Bulunan tek taraflı limitler ve yüksek güvenilirliğe sahip asimptotlar, bu fonksiyonun grafiğinin nasıl göründüğünü varsaymamızı sağlar. Dersin sonunda doğru çizim.
Örnek 8
Bir fonksiyonun grafiğinin asimptotlarını bulun
Bu, bağımsız bir çözüm için bir örnektir, bazı limitleri hesaplamanın rahatlığı için, payı paydaya göre terime bölebilirsiniz. Ve yine, elde edilen sonuçları analiz ederek, bu fonksiyonun bir grafiğini çizmeye çalışın.
Açıktır ki, "gerçek" eğik asimptotların sahipleri, payın en yüksek derecesi olan kesirli rasyonel fonksiyonların grafikleridir. bir tane daha paydanın en yüksek derecesi. Daha büyükse, eğik asimptot artık mevcut olmayacaktır (örneğin,).
Ama hayatta başka mucizeler de olur:
Örnek 9

Çözüm: işlev sürekli tam sayı doğrusunda, yani dikey asimptot yoktur. Ama eğilimli olanlar da olabilir. Kontrol ediyoruz:
Üniversitede benzer bir işlevle nasıl karşılaştığımı hatırlıyorum ve eğik bir asimptotu olduğuna inanamadım. İkinci sınırı bulana kadar:
Açıkçası, iki belirsizlik var: ve öyle ya da böyle, makalenin 5-6. Örneklerinde tartışılan çözüm yöntemini kullanmanız gerekiyor. sınırlar hakkında artan karmaşıklık
... Aşağıdaki formülü kullanmak için eşlenik ifadeyle çarpar ve böleriz:

Cevap:
Belki de en popüler eğik asimptot.
Şimdiye kadar, sonsuzluk "herkese uyan tek bir boyut kesebildi", ancak fonksiyonun grafiğinin iki farklı eğik asimptotlar ve şu noktalarda:
Örnek 10
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin

Çözüm: radikal ifade pozitiftir, yani ihtisas- gerçekten herhangi bir sayı ve dikey çubuklar olamaz.
Eğik asimptot olup olmadığını kontrol edelim.
"x", "eksi sonsuz" olma eğilimindeyse, o zaman:
(altında bir "x" yaparken Kare kök eksi paydayı kaybetmemek için bir eksi işareti eklemek gerekir)
Alışılmadık görünüyor, ancak burada belirsizlik "sonsuz eksi sonsuzluk". Payı ve paydayı eşlenik ifadeyle çarpın:
Bu nedenle, düz çizgi, 'deki grafiğin eğik bir asimptotudur.
"Artı sonsuz" ile her şey daha önemsizdir:

Ve düz çizgi konumunda.
Cevap:
Eğer ;
, Eğer .
Grafik görüntüye dayanamıyorum:

Bu dallardan biri abartma .
Asimptotların potansiyel varlığının başlangıçta sınırlı olması nadir değildir. fonksiyon kapsamı:
Örnek 11
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin
Çözüm: belli ki  , bu nedenle, sadece fonksiyonun grafiğinin olduğu sağ yarım düzlemi dikkate alıyoruz.
, bu nedenle, sadece fonksiyonun grafiğinin olduğu sağ yarım düzlemi dikkate alıyoruz.
1) İşlev sürekli aralıkta, yani eğer dikey asimptot varsa, o zaman sadece ordinat ekseni olabilir. Noktaya yakın fonksiyonun davranışını inceleyelim. sağda:
Not, belirsizlik YOK(yazının başında bu tür durumlara dikkat çekilmiştir) Limit çözme yöntemleri).
Böylece, düz çizgi (ordinat ekseni), fonksiyonun grafiği için dikey asimptottur.
2) Eğik asimptot çalışması tam şemaya göre yapılabilir, ancak makalede Lopital kurallar logaritmik olandan daha yüksek bir büyüme mertebesine sahip doğrusal bir fonksiyonun olduğunu bulduk, bu nedenle:  (aynı dersten Örnek 1'e bakın).
(aynı dersten Örnek 1'e bakın).
Sonuç: apsis ekseni, fonksiyonun grafiğinin yatay asimptotudur.
Cevap:
Eğer ;
, Eğer .
Netlik için çizim:

Görünüşte benzer bir fonksiyonun hiçbir asimptotu olmaması ilginçtir (isteyenler bunu kontrol edebilir).
Son iki kendi kendine çalışma örneği:
Örnek 12
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin

Dikey asimptotları kontrol etmek için önce bulmanız gerekir. fonksiyon alanı ve sonra "şüpheli" noktalarda bir çift tek taraflı limit hesaplayın. Fonksiyon "artı" ve "eksi" sonsuzda tanımlandığı için eğik asimptotlar da hariç tutulmaz.
Örnek 13
Asimptotların varlığı için bir fonksiyonun grafiğini inceleyin
Ve burada sadece eğik asimptotlar olabilir ve yönler ayrı ayrı düşünülmelidir.
Umarım istediğiniz asimptotu bulmuşsunuzdur =)
Başarılar dilerim!
Çözümler ve Cevaplar:
Örnek 2:Çözüm
:
... Tek taraflı limitleri bulalım:

Düz fonksiyonun grafiğinin dikey asimptotu .
2) Eğik asimptotlar.

Düz .
Cevap:
Resim çizme
Örnek 3'e:

Örnek 4:Çözüm
:
1) Dikey asimptotlar. Fonksiyon bir noktada sonsuz olarak kırılır ... Tek taraflı limitleri hesaplayalım:
Not: çift kuvvette sonsuz küçük negatif sayı, sonsuz küçük pozitif sayıya eşittir: .
Düz fonksiyonun grafiğinin dikey asimptotudur.
2) Eğik asimptotlar.

Düz (apsis ekseni), fonksiyonun grafiğinin yatay asimptotudur. .
Cevap:
- (Yunancadan. neg. sık sık ve birbirine denk gelen belirtiler). Sürekli olarak bir eğriye yaklaşan ve onunla yalnızca sonsuzda buluşan düz bir çizgi. Rus dilinde yer alan yabancı kelimeler sözlüğü. Chudinov AN, 1910. ASYMPTOT ... ... Rus dilinin yabancı kelimeler sözlüğü
ASİMPTOT- (Yunanca asimptotolardan örtüşmeyen), eğrinin sonsuz dalının süresiz olarak yaklaştığı düz bir çizgi, örneğin bir hiperbolün asimptotu ... Modern ansiklopedi
ASİMPTOT- (Yunanca asimptotlardan çakışmayan) sonsuz dalı olan bir eğrinin, bu dalın sınırsız olarak yaklaştığı düz bir çizgi, örneğin bir hiperbolün asimptotu ... Büyük Ansiklopedik Sözlük
asimptot- Eğrinin kademeli olarak yaklaştığı düz bir çizgi. asimptot Sonsuz bir dalı olan bir fonksiyonun eğrisinin, argümanı sınırsız bir şekilde arttığında veya ... Teknik çevirmen kılavuzu
asimptot- (Yunanca çakışık olmayan asimptotolardan), eğrinin sonsuz dalının belirsiz bir şekilde yaklaştığı düz bir çizgi, örneğin bir hiperbolün asimptotu. ... Resimli Ansiklopedik Sözlük
ASİMPTOT- kadın, geom. her zaman bir eğriye yaklaşan (hiperbol), ancak asla onunla yakınlaşmayan düz bir çizgi. Bunu açıklamak için bir örnek: eğer herhangi bir sayı ikiye bölünürse, sonsuza kadar azalır ama asla sıfır olmaz. ... ... açıklayıcı sözlük Dahl
asimptot- isim, eşanlamlı sayısı: 1 satır (182) ASIS eşanlamlı sözlüğü. V.N. Trişin. 2013... eşanlamlı sözlük
asimptot- (Yunanca kelimelerden: a, sun, piptw) uyumsuz. Asimptot, süresiz olarak uzatıldığında, ortak çizgiler arasındaki mesafenin daha az olması için belirli bir eğri çizgiye veya onun bir kısmına yaklaşan bir çizgi anlamına gelir ... ...
asimptot- yüzey, yüzeyi en az iki sonsuz uzak noktada kesen düz bir çizgidir ... Brockhaus ve Efron Ansiklopedisi
ASİMPTOT- (asimptot) Bu işlevin argümanı (argümanı) değiştirirken eğiliminde olduğu, ancak argümanın herhangi bir sonlu değeri için ona ulaşmadığı değer. Örneğin, x çıktısının toplam maliyeti TC = a + bx fonksiyonu tarafından veriliyorsa, burada a ve b sabittir ... Ekonomik Sözlük
asimptot- argümanı süresiz olarak arttığında veya azaldığında, sonsuz bir dalı olan bir fonksiyonun eğrisinin yöneldiği (asla ona ulaşmayan) düz bir çizgi. Örneğin, y = c + 1 / x fonksiyonunda, y'nin değeri ... ...'den yaklaşır. Ekonomi ve Matematik Sözlüğü
Bir fonksiyonun asimptot grafiği y = f (x), (x, f (x)) noktasından bu düz çizgiye olan mesafenin, grafik noktasının orijinden sınırsız bir mesafe ile sıfıra meyilli olması özelliği ile düz bir çizgi olarak adlandırılır.
Şekil 3.10. grafik örnekler verilmiştir dikey, yatay ve eğik asimptotlar.
Grafik asimptotlarının bulunması aşağıdaki üç teoreme dayanmaktadır.
Dikey Asimptot Teoremi. y = f (x) fonksiyonu x 0 noktasının bir komşuluğunda tanımlansın (muhtemelen bu noktanın kendisi hariç) ve fonksiyonun tek taraflı limitlerinden en az biri sonsuza eşittir, yani. O zaman x = x 0 düz çizgisi, y = f (x) fonksiyonunun grafiğinin dikey asimptotudur.
Açıkçası, fonksiyon x 0 noktasında sürekli ise x = x 0 düz çizgisi dikey bir asimptot olamaz, çünkü bu durumda  ... Sonuç olarak, düşey asimptotlar, fonksiyonun süreksizlik noktalarında veya tanım alanının uçlarında aranmalıdır.
... Sonuç olarak, düşey asimptotlar, fonksiyonun süreksizlik noktalarında veya tanım alanının uçlarında aranmalıdır.
Yatay asimptot teoremi. Yeterince büyük x için y = f (x) fonksiyonu tanımlansın ve fonksiyonun sonlu bir limiti vardır. O zaman düz çizgi y = b, fonksiyonun grafiğinin yatay asimptotudur.
Yorum Yap. Sınırlardan sadece biri sonlu ise, fonksiyon sırasıyla sol taraf veya sağ taraf Yatay asimptot.
Bu durumda, fonksiyon eğik bir asimptota sahip olabilir.
Eğik Asimptot Teoremi. Yeterince büyük x için y = f (x) fonksiyonu tanımlansın ve sonlu limitler var  ... O zaman y = kx + b düz çizgisi, fonksiyonun grafiğinin eğik asimptotudur.
... O zaman y = kx + b düz çizgisi, fonksiyonun grafiğinin eğik asimptotudur.
Kanıt yok.
Eğik asimptot ve yatay, karşılık gelen sınırların tabanı belirli bir işaretin sonsuzluğunu içeriyorsa, sağ veya solak olabilir.
Fonksiyonları incelemek ve grafiklerini çizmek genellikle aşağıdaki adımları içerir:
1. Fonksiyonun tanım kümesini bulun.
2. Düzgünlük-teklik fonksiyonunu araştırın.
3. Süreksizlik noktalarını inceleyerek düşey asimptotları ve eğer sonlu ise fonksiyonun tanım alanının sınırları üzerindeki davranışını bulunuz.
4. Fonksiyonun sonsuzdaki davranışını inceleyerek yatay veya eğik asimptotları bulun.
5. Fonksiyonun monotonluğunun ekstremum ve aralıklarını bulun.
6. Fonksiyonun dışbükeylik aralıklarını ve büküm noktalarını bulunuz.
7. Koordinat eksenleriyle kesişme noktalarını ve muhtemelen grafiği iyileştiren bazı ek noktaları bulun.
diferansiyel fonksiyon
Bir fonksiyonun belirli bir taban için sonlu bir sayısı varsa, o zaman bu sayının toplamı ve aynı taban için sonsuz küçük bir değer olarak gösterilebileceği kanıtlanabilir (ve tersi):
Bu teoremi türevlenebilir bir fonksiyona uygularız:
Böylece, Dу fonksiyonunun artışı iki terimden oluşur: 1) Dх'ye göre doğrusal, yani. f`(x)Dx; 2) Dx'e göre doğrusal olmayan, yani. bir (Dx) Dx. Ayrıca, o zamandan beri  , bu ikinci terim Dx'ten daha yüksek bir mertebeden sonsuz küçüktür (Dx sıfıra eğilimli olduğundan, daha da hızlı sıfıra eğilim gösterir).
, bu ikinci terim Dx'ten daha yüksek bir mertebeden sonsuz küçüktür (Dx sıfıra eğilimli olduğundan, daha da hızlı sıfıra eğilim gösterir).
Diferansiyel fonksiyon ana olarak adlandırılır, fonksiyonun artışının Dx kısmına göre doğrusal, türevin ürününe eşit ve bağımsız değişken dy = f `(x) Dx.
y = x fonksiyonunun diferansiyelini bulalım.
dy = f `(x) Dx = x`Dx = Dx olduğundan, dx = Dx, yani bağımsız değişkenin diferansiyeli bu değişkenin artışına eşittir.
Bu nedenle, bir fonksiyonun diferansiyeli formülü dy = f `(x) dx şeklinde yazılabilir. Bu nedenle türevin gösterimlerinden biri dy / dx kesridir.

Diferansiyelin geometrik anlamı gösterilmiştir.
Şekil 3.11. y = f (x) fonksiyonunun grafiğinde keyfi bir M (x, y) noktası alın. x argümanına bir artış Dx verelim. Daha sonra y = f (x) işlevi, Dy = f (x + Dх) - f (x) artışını alacaktır. Apsis ekseninin pozitif yönü ile bir a açısı oluşturan M noktasındaki fonksiyonun grafiğine bir teğet çizelim, yani. f`(x) = tg a. İtibaren sağ üçgen MKN
KN = MN * tg a = Dх * tg a = f `(x) Dх = dy.
Böylece, bir fonksiyonun diferansiyeli, verilen bir noktada fonksiyonun grafiğine çizilen tanjantın ordinatının, x'in bir Dx artışı aldığındaki artışıdır.
Diferansiyelin özellikleri temel olarak türevinkilerle aynıdır:
3.d (u ± v) = du ± dv.
4.d (uv) = v du + u dv.
5.d (u / v) = (v du - u dv) / v 2.
Ancak, bir fonksiyonun diferansiyelinin türevinin sahip olmadığı önemli bir özelliği vardır - bu diferansiyel form değişmezliği.
y = f (x) fonksiyonunun diferansiyel tanımından, diferansiyel dy = f `(x) dx'tir. Bu fonksiyon y karmaşıksa, yani. y = f (u), burada u = j (x), o zaman y = f ve f `(x) = f` (u) * u`. Sonra dy = f `(u) * u`dx. Ama işlev için
u = j (x) diferansiyel du = u`dx. Dolayısıyla dy = f `(u) * du.
dy = f `(x) dx ve dy = f` (u) * du eşitliklerini karşılaştırarak, bağımsız değişken x'in bir fonksiyonu yerine bir fonksiyonunu düşünürsek, diferansiyel formülün değişmediğinden emin olacağız. bağımlı değişken u. Diferansiyelin bu özelliğine, diferansiyelin formunun (veya formülünün) değişmezliği (yani değişmezliği) denir.
Bununla birlikte, bu iki formülün hala bir farkı vardır: birincisinde, bağımsız değişkenin diferansiyeli bu değişkenin artışına eşittir, yani. dx = Dx ve ikincisinde, du işlevinin diferansiyeli, bu Du işlevinin artışının yalnızca doğrusal kısmıdır ve yalnızca küçük Dx du »Du için.