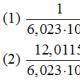Leibniz'in formülü şu şekilde verilir: n'yi hesaplamak iki fonksiyonun çarpımının türevi. Kanıtı iki şekilde verilir. n. dereceden türevin hesaplanmasına ilişkin bir örnek ele alınmıştır.

Ayrıca bakınız: İki fonksiyonun çarpımının türevi

Leibniz formülü

Leibniz formülünü kullanarak, iki fonksiyonun çarpımının n. dereceden türevi hesaplanabilir. Şuna benziyor:
(1) ,
nerede
- binom katsayıları.

Binom katsayıları, binomun ve güçlerindeki genişleme katsayılarıdır:
.
Ayrıca sayı, n'den k'ye kadar olan kombinasyonların sayısıdır.

Leibniz'in formülünün kanıtı

İki fonksiyonun çarpımının türevi için formülü uygularız:
(2) .
Formül (2)'yi aşağıdaki gibi yeniden yazalım:
.
Yani, bir fonksiyonun x değişkenine, diğerinin y değişkenine bağlı olduğunu düşünüyoruz. Hesaplamanın sonunda, varsayıyoruz. O zaman önceki formül şu şekilde yazılabilir:
(3) .
Türev, terimlerin toplamına eşit olduğundan ve her terim iki fonksiyonun çarpımı olduğundan, daha yüksek dereceli türevleri hesaplamak için kuralı (3) tutarlı bir şekilde uygulayabilirsiniz.

O zaman n'inci mertebenin türevi için:

.
Bunu göz önünde bulundurarak Leibniz formülünü elde ederiz:
(1) .

Tümevarımla ispat

Leibniz formülünün ispatını matematiksel tümevarım yöntemiyle sunalım.

Leibniz'in formülünü yeniden yazalım:
(4) .
n = 1 için:
.
Bu, iki fonksiyonun çarpımının türevinin formülüdür. O adil.

Formül (4)'ün n'inci dereceden türev için geçerli olduğunu varsayalım. n + türevi için geçerli olduğunu kanıtlayalım. 1 sıra.

Farklılaştır (4):
;



.
Böylece bulduk:
(5) .

(5)'te değiştirin ve şunları dikkate alın:

.
Bu, formül (4)'ün n + türevi için aynı forma sahip olduğunu gösterir. 1 sıra.

Yani formül (4) n = için geçerlidir 1 ... Tuttuğu varsayımından, n = m bazı sayıları için n = m + için geçerli olduğu sonucu çıkar. 1 .
Leibniz'in formülü kanıtlanmıştır.

Örnek

Hesaplamak n'inci türev işlev
.

Leibniz formülünü uyguluyoruz
(2) .
bizim durumumuzda
;
.

Türev tablosuna göre, elimizde:
.
Trigonometrik fonksiyonların özelliklerini uygularız:
.
Sonra
.
Dolayısıyla sinüs fonksiyonunun farklılaşmasının onun ile kaymasına yol açtığı görülmektedir. Sonra
.

Fonksiyonun türevlerini bulun.
;
;
;
, .

noktasından beri, Leibniz formülündeki sadece ilk üç terim sıfırdan farklıdır. Binom katsayılarını bulun.
;
.

Leibniz formülüne göre:

.

Çözüm uygulamalı görevler integrali hesaplamaya indirgenir, ancak bunu tam olarak yapmak her zaman mümkün değildir. Bazen anlamını bilmen gerekir kesin integral bir dereceye kadar doğrulukla, örneğin binde birine kadar.

Belirli bir integralin yaklaşık değerini gerekli doğrulukla bulmanın gerekli olacağı sorunlar vardır, o zaman Simposna yöntemi, yamuklar, dikdörtgenler gibi sayısal entegrasyon kullanılır. Tüm durumlar, belirli bir doğrulukla hesaplamamıza izin vermez.

Bu makale Newton-Leibniz formülünün uygulamasını incelemektedir. Bu, belirli integrali doğru bir şekilde hesaplamak için gereklidir. Verilmiş olacak detaylı örnekler, belirli bir integralde değişkenin değişimini ele alıyoruz ve belirli integralin kısımlar halinde integralini alırken değerlerini buluyoruz.

Newton-Leibniz formülü

y = y (x) fonksiyonu [a; b] ve F (x) bu segmentin fonksiyonunun ters türevlerinden biridir, o zaman Newton-Leibniz formülü adil sayılır. ∫ a b f (x) d x = F (b) - F (a) olarak yazarız.

Bu formül kabul edilir integral hesabın temel formülü.

Bu formülü kanıtlamak için, mevcut bir değişken üst limiti olan bir integral kavramını kullanmak gerekir.

y = f (x) fonksiyonu [a; b], sonra x ∈ a argümanının değeri; b ve integral ∫ a x f (t) d t şeklindedir ve üst sınırın bir fonksiyonu olarak kabul edilir. ∫ axf (t) dt = Φ (x) şeklinde olacak fonksiyonun notasyonunu almak gerekir, süreklidir ve formun eşitsizliği ∫ axf (t) dt "= Φ" (x) = f (x) bunun için geçerlidir.

Φ (x) fonksiyonunun artışının ∆ x argümanının artışına karşılık geldiğini sabitleyelim, belirli integralin beşinci ana özelliğini kullanmak ve elde etmek gerekir.

Φ (x + ∆ x) - Φ x = ∫ ax + ∆ xf (t) dt - ∫ axf (t) dt = = ∫ ax + ∆ xf (t) dt = f (c) x + ∆ x - x = f (c) ∆ x

burada c ∈ x değeri; x + ∆ x.

Φ (x + ∆ x) - Φ (x) ∆ x = f (c) biçiminde bir eşitlik belirleyelim. Bir fonksiyonun türevinin tanımıyla, ∆ x → 0 olarak sınıra geçmek gerekir, daha sonra Φ "(x) = f (x) biçiminde bir formül elde ederiz. Bunu elde ederiz Φ (x) [a;b] üzerinde bulunan y = f (x) formunun bir fonksiyonu için ters türevlerden biridir.Aksi halde ifade yazılabilir

F (x) = Φ (x) + C = ∫ a x f (t) d t + C, burada C değeri sabittir.

Belirli integralin birinci özelliğini kullanarak F(a)'yı hesaplayalım. O zaman bunu alırız

F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C, dolayısıyla C = F (a) elde ederiz. Sonuç F (b) hesaplanırken uygulanır ve şunu elde ederiz:

F (b) = Φ (b) + C = ∫ abf (t) dt + C = ∫ abf (t) dt + F (a), diğer bir deyişle, F (b) = ∫ abf (t) dt + F (a). Eşitlik Newton-Leibniz formülünü kanıtlar ∫ a b f (x) d x + F (b) - F (a).

Fonksiyonun artışı F x a b = F (b) - F (a) olarak alınır. Notasyonun yardımıyla Newton-Leibniz formülü ∫ a b f (x) d x = F x a b = F (b) - F (a) şeklini alır.

Formülü uygulamak için, [a; b], bu segmentten terstürevin artışını hesaplayın. Newton-Leibniz formülünü kullanarak birkaç örnek hesaplama düşünün.

örnek 1

Newton-Leibniz formülünü kullanarak belirli integrali ∫ 1 3 x 2 d x hesaplayın.

Çözüm

y = x 2 formunun integralinin [1; 3], o zaman bu segmentte integrallenebilir. Belirsiz integraller tablosundan, y = x 2 fonksiyonunun, x'in tüm gerçek değerleri için bir ters türev kümesine sahip olduğunu görüyoruz, dolayısıyla x ∈ 1; 3 F (x) = ∫ x 2 d x = x 3 3 + C olarak yazılacaktır. C = 0 olan ters türevi almak gerekir, o zaman F (x) = x 3 3 elde ederiz.

Newton-Leibniz formülünü kullanalım ve belirli integralin hesaplanmasının ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 - 1 3 3 = 26 3 şeklini alacağını alalım.

Cevap:∫ 1 3 x 2 d x = 26 3

Örnek 2

Newton-Leibniz formülünü kullanarak ∫ - 1 2 x · e x 2 + 1 d x belirli integralini hesaplayın.

Çözüm

Verilen fonksiyon [- 1; 2], bu yüzden üzerinde integrallenebilir. Belirsiz integral ∫ x ex 2 + 1 dx'in değerini diferansiyel işaretin altına getirme yöntemini kullanarak bulmak gerekir, sonra ∫ x ex 2 + 1 dx = 1 2 ∫ ex 2 + 1 d (x 2 elde ederiz) + 1) = 1 2 ör 2 + 1 + C.

Dolayısıyla, y = x · e x 2 + 1 fonksiyonunun tüm x, x ∈ - 1 için geçerli olan bir ters türevleri kümesine sahibiz; 2.

C=0'da ters türevi almak ve Newton-Leibniz formülünü uygulamak gerekir. Sonra formun bir ifadesini alırız

∫ - 1 2 x ex 2 + 1 dx = 1 2 ex 2 + 1 - 1 2 = = 1 2 e 2 2 + 1 - 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 - 1)

Cevap:∫ - 1 2 x e x 2 + 1 d x = 1 2 e 2 (e 3 - 1)

Örnek 3

∫ - 4 - 1 2 4 x 3 + 2 x 2 d x ve ∫ - 1 1 4 x 3 + 2 x 2 d x integrallerini hesaplayın.

Çözüm

Bölüm - 4; - 1 2, integral işaretinin altındaki fonksiyonun sürekli olduğunu, yani integrallenebilir olduğunu gösterir. Buradan y = 4 x 3 + 2 x 2 fonksiyonunun ters türevleri kümesini buluruz. anladık

∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x - 2 d x = 2 x 2 - 2 x + C

F (x) = 2 x 2 - 2 x ters türevini almak gerekir, daha sonra Newton-Leibniz formülünü uygulayarak hesapladığımız integrali elde ederiz:

∫ - 4 - 1 2 4 x 3 + 2 x 2 dx = 2 x 2 - 2 x - 4 - 1 2 = 2 - 1 2 2 - 2 - 1 2 - 2 - 4 2 - 2 - 4 = 1 2 + 4 - 32 - 1 2 = - 28

İkinci integralin hesaplanmasına geçiş yapıyoruz.

Segmentinden [- 1; 1] integralin sınırsız olduğu kabul edilir, çünkü lim x → 0 4 x 3 + 2 x 2 = + ∞, o zaman şu şekildedir: gerekli kondisyon bir segmentten bütünleştirilebilirlik. O halde F(x) = 2 x 2 - 2 x, [- 1; 1], çünkü O noktası segmente aittir, ancak tanım alanına dahil değildir. Bu, y = 4 x 3 + 2 x 2 fonksiyonu için [- 1; 1 ].

Cevap: ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x = - 28,[- 1; 1 ].

Newton-Leibniz formülünü kullanmadan önce, belirli bir integralin varlığını tam olarak bilmeniz gerekir.

Belirli bir integralde bir değişkenin değişimi

y = f (x) fonksiyonu belirli ve [a; b], ardından mevcut küme [a; b], α segmentinde tanımlanan x = g (z) fonksiyonunun değer aralığı olarak kabul edilir; g (α) = a ve g β = b olduğu mevcut sürekli türev ile β, bundan elde ederiz ki ∫ abf (x) dx = ∫ α β f (g (z)) · g "(z) d z .

Bu formül, belirsiz integralin ∫ f (x) d x biçiminde olduğu, ∫ a b f (x) d x integralini hesaplamak gerektiğinde kullanılır, ikame yöntemi kullanılarak hesaplanır.

Örnek 4

∫ 9 18 1 x 2 x - 9 d x biçiminde belirli bir integral hesaplayın.

Çözüm

İntegrant, integrasyon aralığında sürekli olarak kabul edilir, bu da varoluş için belirli bir integralin gerçekleştiği anlamına gelir. 2 x - 9 = z ⇒ x = g (z) = z 2 + 9 2 olduğunu belirleyelim. x = 9 değeri, z = 2 9 - 9 = 9 = 3 anlamına gelir ve x = 18 için z = 2 18 - 9 = 27 = 3 3, sonra g α = g (3) = 9 olur, g β = g 3 3 = 18. Elde edilen değerleri ∫ a b f (x) d x = ∫ α β f (g (z)) g "(z) d z formülüne koyarak, elde ederiz

∫ 9 18 1 x 2 x - 9 dx = ∫ 3 3 3 1 z 2 + 9 2 z z 2 + 9 2 "dz = = ∫ 3 3 3 1 z 2 + 9 2 z zdz = ∫ 3 3 3 2 z 2 + 9 gün

Belirsiz integraller tablosuna göre, 2 z 2 + 9 fonksiyonunun ters türevlerinden birinin 2 3 a r c t g z 3 değerini aldığını görüyoruz. Daha sonra Newton-Leibniz formülünü uygulayarak elde ederiz.

∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 - 2 3 a r c t g 3 3 = 2 3 a r c t g 3 - bir r c t g 1 = 2 3 π 3 - π 4 = π 18

Bulgu, ∫ a b f (x) d x = ∫ α β f (g (z)) · g "(z) d z formülü kullanılmadan yapılabilir.

Yerine koyma yönteminde ∫ 1 x 2 x - 9 d x biçiminde bir integral kullanılırsa, ∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C sonucuna ulaşılabilir.

Buradan Newton-Leibniz formülünü kullanarak hesaplamalar yapacağız ve belirli bir integral hesaplayacağız. anladık

∫ 9 18 2 z 2 + 9 dz = 2 3 arktgz 3 9 18 = = 2 3 arktan 2 18 - 9 3 - arktan 2 9 - 9 3 = = 2 3 arktan 3 - arktan 1 = 2 3 π 3 - π 4 = π 18

Sonuçlar eşleşti.

Cevap: ∫ 9 18 2 x 2 x - 9 d x = π 18

Belirli bir integral hesaplanırken parçalara göre entegrasyon

Segmentinde ise [a; b], u (x) ve v (x) fonksiyonları tanımlı ve süreklidir, o zaman birinci mertebeden türevleri v "(x) · u (x) integrallenebilirdir, dolayısıyla bu aralıktan integrallenebilir fonksiyon u" (x) için ) · v ( x) eşitliği ∫ abv "(x) u (x) dx = (u (x) v (x)) ab - ∫ abu" (x) v (x) dx doğrudur.

Formül daha sonra kullanılabilir, ∫ a b f (x) d x integralini hesaplamak gerekir ve ∫ f (x) d x onu parçalara göre entegrasyon yoluyla aramak gerekliydi.

Örnek 5

Belirli integrali ∫ - π 2 3 π 2 x · sin x 3 + π 6 d x hesaplayın.

Çözüm

x · sin x 3 + π 6 işlevi - π 2 aralığında integrallenebilir; 3 π 2, yani süreklidir.

u (x) = x olsun, sonra d (v (x)) = v "(x) dx = günah x 3 + π 6 dx ve d (u (x)) = u" (x) dx = dx, ve v (x) = - 3 cos π 3 + π 6. ∫ a b v "(x) u (x) d x = (u (x) v (x)) a b - ∫ a b u" (x) v (x) d x formülünden elde ederiz

∫ - π 2 3 π 2 x günah x 3 + π 6 dx = - 3 x cos x 3 + π 6 - π 2 3 π 2 - ∫ - π 2 3 π 2 - 3 cos x 3 + π 6 dx = = - 3 3 π 2 cos π 2 + π 6 - - 3 - π 2 cos - π 6 + π 6 + 9 günah x 3 + π 6 - π 2 3 π 2 = 9 π 4 - 3 π 2 + 9 günah π 2 + π 6 - günah - π 6 + π 6 = 9 π 4 - 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2

Örnek başka bir şekilde çözülebilir.

Newton-Leibniz formülünü kullanarak x sin x 3 + π 6 fonksiyonunun ters türevleri kümesini parçalara göre integral alarak bulun:

∫ x günah xx 3 + π 6 dx = u = x, dv = günah x 3 + π 6 dx ⇒ du = dx, v = - 3 cos x 3 + π 6 = = - 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 dx = = - 3 x cos x 3 + π 6 + 9 günah x 3 + π 6 + C ⇒ ∫ - π 2 3 π 2 x günah x 3 + π 6 dx = - 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 - - - 3 - π 2 cos - π 6 + π 6 + 9 sin - π 6 + π 6 = = 9 π 4 + 9 3 2 - 3 π 2 - 0 = 3 π 4 + 9 3 2

Cevap: ∫ x günah x x 3 + π 6 d x = 3 π 4 + 9 3 2

Metinde bir hata fark ederseniz, lütfen seçin ve Ctrl + Enter tuşlarına basın

Eserin metni, resim ve formüller olmadan yerleştirilmiştir.
Tam versiyonçalışma, PDF formatında "İş dosyaları" sekmesinde mevcuttur

"Bana da Newton'un iki terimlisi!»

"Usta ve Margarita" romanından

“Pascal üçgeni o kadar basittir ki, on yaşındaki bir çocuk bile bunu yazabilir. Aynı zamanda, tükenmez hazineleri gizler ve matematiğin ilk bakışta ortak hiçbir yanı olmayan çeşitli yönlerini birbirine bağlar. Yani olağandışı özellikler Pascal üçgenini tüm matematikteki en zarif şemalardan biri olarak düşünmemize izin verin "

Martin Gardner.

İşin amacı: azaltılmış çarpma için formülleri genelleştirmek, problem çözme uygulamalarını göstermek.

Görevler:

1) bu konudaki bilgileri incelemek ve sistematik hale getirmek;

2) Newton binomunun uygulanmasına ilişkin problem örneklerini ve derecelerin toplamı ve farkı için formülleri analiz eder.

Araştırma nesneleri: Newton'un iki terimi, güçlerin toplamı ve farkı için formüller.

Araştırma Yöntemleri:

Eğitim ve popüler bilim literatürü, İnternet kaynakları ile çalışın.

Hesaplamalar, karşılaştırma, analiz, analoji.

alaka. Bir kişi genellikle, bazı nesneleri yerleştirmenin tüm olası yollarının sayısını veya bazı eylemleri gerçekleştirmenin tüm olası yollarının sayısını saymanın gerekli olduğu görevlerle uğraşmak zorundadır. Bir kişinin seçmesi gereken farklı yollar veya seçenekler, çok çeşitli kombinasyonlara kadar uzanır. Ve kombinatorik adı verilen bütün bir matematik dalı, şu ya da bu durumda kaç tane kombinasyon olduğu soruların cevaplarını aramakla meşgul.

Pek çok uzmanlığın temsilcileri kombinatoryal miktarlarla uğraşmak zorundadır: bir kimyager, biyolog, tasarımcı, sevk memuru, vb. Son yıllarda kombinatoriklere artan ilgi, sibernetik ve bilgisayar teknolojisinin hızlı gelişmesinden kaynaklanmaktadır.

Tanıtım

Muhatabın karşılaştığı sorunların karmaşıklığını abarttığını vurgulamak istediklerinde, "Ben de Newton'un iki terimlisi var!" diyorlar. Diyelim ki, işte Newton'un iki terimlisi, zor, ama bazı problemleriniz var! İlgi alanları matematikle hiçbir ilgisi olmayan insanlar bile Newton'un iki terimlisini duymuşlardır.

"İki terimli" kelimesi, iki terimli anlamına gelir, yani. iki terimin toplamı Sözde kısaltılmış çarpma formülleri okul kursundan bilinir:

( a+ b) 2 = bir 2 + 2ab + b 2 , (a + b) 3 = bir 3 + 3a 2 b + 3ab 2 + b 3 .

Bu formüllerin genelleştirilmesi, Newton binom formülü adı verilen bir formüldür. Okulda ve formüllerde karelerin farkını, küplerin toplamını ve farkını çarpanlara ayırmak için kullanılır. Başka derecelere genelleme yapıyorlar mı? Evet, bu tür formüller var, genellikle çeşitli problemlerin çözümünde kullanılırlar: bölünebilirliği kanıtlama, kesirleri iptal etme, yaklaşık hesaplamalar.

Genelleme formülleri çalışması, tümdengelimli-matematiksel düşünme ve genel düşünme yeteneklerini geliştirir.

BÖLÜM 1. NEWTON FORMÜLÜNÜN BİNOM

Kombinasyonlar ve özellikleri

X, n elemanlı bir küme olsun. X kümesinin k elemanlı herhangi bir Y alt kümesine, n'den k elemanlı bir kombinasyon, ayrıca k ≤ n denir.

n'den k elemanın farklı kombinasyonlarının sayısı C n k ile gösterilir. Kombinatorikteki en önemli formüllerden biri, С n k sayısı için aşağıdaki formüldür:

Açık kısaltmalardan sonra aşağıdaki gibi yazılabilir:

Özellikle,

Bu, X kümesinin yalnızca bir 0 öğe alt kümesine sahip olması gerçeğiyle oldukça tutarlıdır - boş alt küme.

C n k sayıları bir dizi dikkate değer özelliğe sahiptir.

Aşağıdaki formül geçerlidir: С n k = С n - k n, (3)

Formül (3)'ün anlamı, X'ten gelen tüm k-terimli alt kümeler kümesi ile X'ten gelen tüm (n - k) -terimli alt kümeler kümesi arasında bire bir denklik olmasıdır: bu denkliği kurmak için, her k-terim Y alt kümesi için, X kümesindeki tamamlayıcısıyla eşleşmesi yeterlidir.

C 0 n + C 1 n + C 2 n + ... + C n n = 2 n formülü geçerlidir (4)

Sol taraftaki toplam, X kümesinin tüm alt kümelerinin sayısını ifade eder (C 0 n, 0 terimli alt kümelerin sayısıdır, C 1 n, tek terimli alt kümelerin sayısıdır, vb.).

Herhangi bir k, 1≤ k≤ n için eşitlik

C kn = Cn -1 k + Cn -1 k -1 (5)

Bu eşitliği formül (1) kullanarak elde etmek kolaydır. Aslında,

1.2. Newton'un binom formülünün türetilmesi

Binomun güçlerini düşünün bir +B .

n = 0, (a +B ) 0 = 1

n = 1, (a +B ) 1 = 1a + 1B

n = 2,(bir +B ) 2 = 1a 2 + 2aB +1 B 2

n = 3,(bir +B ) 3 = 1 bir 3 + 3a 2 B + 3aB 2 +1 B 3

n = 4,(bir +B ) 4 = 1a 4 + 4a 3 B + 6a 2 B 2 + 4aB 3 +1 B 4

n = 5,(bir +B ) 5 = 1 A 5 + 5a 4 B + 10a 3 B 2 + 10a 2 B 3 + 5aB 4 + 1 B 5

Aşağıdaki kalıplara dikkat edin:

Elde edilen polinomun üye sayısı, binomun üssünden bir fazladır;

Birinci terimin üssü n'den 0'a düşer, ikinci terimin üssü 0'dan n'ye yükselir;

Tüm tek terimlilerin dereceleri, durumdaki iki terimlinin derecelerine eşittir;

Her tek terimli, birinci ve ikinci ifadelerin çeşitli derecelerdeki ve belirli bir sayıdaki çarpımıdır - binom katsayısı;

Genişlemenin başlangıcından ve sonundan eşit uzaklıkta olan binom katsayıları eşittir.

Bu formüllerin genelleştirilmesi, Newton binom formülü olarak adlandırılan aşağıdaki formüldür:

(a + B ) n = C 0 n a n B 0 + C 1 n a n -1 B + C 2 n a n -2 B 2 + ... + C n -1 n ab n -1 + C n n a 0 B n . (6)

Bu formülde n herhangi bir doğal sayı olabilir.

Formül (6) türetelim. Öncelikle şunu yazalım:

(a + B ) n = (a + B )(a + B ) ... (a + B ), (7)

çarpılacak parantez sayısı nerede n... Toplamı toplamla çarpmaya yönelik olağan kuraldan, (7) ifadesinin, aşağıdaki gibi oluşturulabilecek tüm olası ürünlerin toplamına eşit olduğu sonucu çıkar: Toplamların ilkindeki herhangi bir terim bir + b ikinci toplamdaki herhangi bir terimle çarpılır bir + b, üçüncü toplamdaki herhangi bir terim için vb.

Söylenenlerden açıkça anlaşılmaktadır ki, ifadedeki terim (a + B ) n harflerden oluşan n uzunluğundaki (bire bir) dizeleri eşleştir a ve B. Terimler arasında benzer terimler olacaktır; bu tür üyelerin aynı sayıda harf içeren dizilere karşılık geldiği açıktır. a... Ancak harfi tam olarak k kez içeren satır sayısı a, eşittir C n k. Bu nedenle, a harfini içeren tüm terimlerin toplamı tam olarak k kez bir faktörle С n k'ye eşittir. a n - k B k . k 0, 1, 2,…, n-1, n değerlerini alabildiğinden, akıl yürütmemizden formül (6) gelir. (6)'nın daha kısa yazılabileceğine dikkat edin: (8)

Formül (6) Newton adıyla anılsa da gerçekte Newton'dan önce keşfedilmiştir (örneğin Pascal bunu biliyordu). Newton'un değeri, tamsayı olmayan göstergeler için bu formülün bir genellemesini bulması gerçeğinde yatmaktadır. 1664-1665'te I. Newton'du. keyfi kesirli ve negatif üsler için bir binom derecesini ifade eden bir formül türetmiştir.

Formül (6)'da yer alan C 0 n, C 1 n, ..., C n n sayılarına genellikle binom katsayıları denir ve bunlar aşağıdaki gibi tanımlanır:

Bu katsayıların bir takım özellikleri formül (6)'dan elde edilebilir. Örneğin, koyarak a= 1, b = 1, şunu elde ederiz:

2 n = C 0 n + C 1 n + C 2 n + C 3 n + ... + C n n,

onlar. formül (4). eğer koyarsak a= 1, b = -1, o zaman şunları elde ederiz:

0 = C 0 n - C 1 n + C 2 n - C 3 n + ... + (-1) n C n n

veya C 0 n + C 2 n + C 4 n + ... = C 1 n + C 3 n + + C 5 n + ....

Bu, açılımın çift terimlerinin katsayılarının toplamının, açılımın tek terimlerinin katsayılarının toplamına eşit olduğu anlamına gelir; her biri 2 n -1'e eşittir.

Genişlemenin uçlarından eşit uzaklıkta bulunan terimlerin katsayıları eşittir. Bu özellik şu ilişkiden çıkar: С n k = С n n - k

İlginç bir özel durum

(x + 1) n = C 0 n x n + C 1 n x n-1 + ... + C k n x n - k + ... + C n n x 0

veya daha kısa (x +1) n = ∑C n k x n - k.

1.3. polinom teoremi

Teorem.

Kanıt.

Parantezleri genişlettikten sonra tek terimli elde etmek için, alındığı parantezleri, alındığı parantezleri vb. seçmeniz gerekir. ve alındığı parantezler. Benzer terimleri azalttıktan sonra bu tek terimlinin katsayısı sayıya eşit böyle bir seçimin yapılabileceği yollar. Seçimler dizisinin ilk adımı çeşitli şekillerde gerçekleştirilebilir, ikinci adım -, üçüncü adım - ve böyle devam eder, inci adım - şekillerde. İstenen katsayı ürüne eşittir

BÖLÜM 2. Yüksek dereceli türevler.

Daha yüksek derecelerin türevleri kavramı.

Fonksiyonun belirli bir aralıkta türevlenebilir olmasına izin verin. O zaman türevi, genel olarak konuşursak, bağlıdır NS, yani, bir fonksiyonudur NS... Sonuç olarak, onunla ilgili olarak, bir türevin varlığı sorusu tekrar gündeme getirilebilir.

Tanım . Birinci türevin türevi denir ikinci dereceden veya ikinci türevin türevidir ve veya sembolü ile gösterilir, yani

Tanım . İkinci türevin türevi, üçüncü dereceden veya üçüncü dereceden türev olarak adlandırılır ve veya sembolü ile gösterilir.

Tanım . Türevn -inci sıra işlev türevinin birinci türevidir (n -1) - bu fonksiyonun -inci mertebesi ve veya sembolü ile gösterilir:

Tanım . Birinciden daha yüksek mertebeden türevlere denir. daha yüksek türevler.

Yorum Yap... Benzer şekilde, formülü alabilirsiniz n fonksiyonun -th türevi:

Parametrik olarak verilen bir fonksiyonun ikinci türevi

Fonksiyon denklemlerle parametrik olarak verilmişse, ikinci dereceden türevi bulmak için birinci türevinin ifadesinin türevini şu şekilde almak gerekir: karmaşık fonksiyon bağımsız değişken.

O zamandan beri

ve bunu dikkate alarak,

Anlıyoruz, yani.

Üçüncü türev de benzer şekilde bulunabilir.

Toplam, ürün ve bölümün diferansiyeli.

Diferansiyel, türevden bağımsız değişkenin diferansiyeli ile çarpılarak elde edildiğinden, temelin türevlerini bilmek temel fonksiyonlar, türev bulma kurallarının yanı sıra, diferansiyelleri bulmak için de benzer kurallara gelebilir.

1 0 . Diferansiyel sabiti sıfırdır.

2 0 . Sonlu sayıda türevlenebilir fonksiyonun cebirsel toplamının diferansiyeli, bu fonksiyonların diferansiyellerinin cebirsel toplamına eşittir. .

3 0 . İki türevlenebilir fonksiyonun çarpımının diferansiyeli, birinci fonksiyonun, ikinci fonksiyonun diferansiyeli ile ikinci fonksiyonun, birinci fonksiyonun diferansiyeli ile ikinci fonksiyonun ürünlerinin toplamına eşittir. .

Sonuç. Sabit çarpan, diferansiyel işaretinin dışında alınabilir.

2.3. Parametrik olarak tanımlanmış fonksiyonlar, farklılaşmaları.

Tanım . Her iki değişken de varsa, bir işlev parametrik olarak verilir. NS ve y her biri aynı yardımcı değişkenin tek değerli fonksiyonları olarak ayrı ayrı tanımlanır - parametreT :

neredeT içinde değişir.

Yorum Yap ... Bir daire ve bir elipsin parametrik denklemlerini sunalım.

a) Merkezi orijinde ve yarıçapı olan bir daire r parametrik denklemlere sahiptir:

b) Elips için parametrik denklemleri yazalım:

Parametreyi hariç tutarak Tİncelenen doğruların parametrik denklemlerinden kanonik denklemlerine ulaşılabilir.

teorem ... eğer fonksiyon argümandan y x, denklemlerle parametrik olarak verilir, burada ve buna göre türevlenebilirT fonksiyonlar ve sonra.

2.4. Leibniz formülü

türevini bulmak için n iki fonksiyonun çarpımının -inci mertebesi büyük pratik önem Leibniz formülüne sahiptir.

İzin vermek sen ve v- bir değişkenin bazı fonksiyonları NS herhangi bir düzenin türevlerine sahip olmak ve y = UV... ifade edelim n fonksiyonların türevleri cinsinden -th türevi sen ve v .

biz sürekli

Sırasıyla ikinci ve üçüncü türevler için ifadeler ile Newton'un iki terimlisinin ikinci ve üçüncü kuvvetlerdeki açılımı arasındaki analojiyi fark etmek kolaydır, ancak üsler yerine türevin sırasını belirleyen sayılar ve fonksiyonlar vardır. kendileri "sıfır mertebenin türevleri" olarak kabul edilebilir. Bunu akılda tutarak, Leibniz formülünü elde ederiz:

Bu formül matematiksel tümevarım yöntemiyle kanıtlanabilir.

BÖLÜM 3. LEIBNITZ FORMÜLÜNÜN UYGULANMASI.

İki fonksiyonun çarpımının herhangi bir mertebesinin türevini hesaplamak için, iki fonksiyonun çarpımının türevini hesaplamak için formülün sıralı uygulamasını atlayarak, uygulayın. Leibniz formülü.

Bu formülü kullanarak, iki fonksiyonun çarpımının n'inci dereceden türevini hesaplama örneklerini ele alacağız.

Örnek 1.

Fonksiyonun ikinci dereceden türevini bulun

Tanım olarak, ikinci türev, birinci türevin birinci türevidir, yani

Bu nedenle, önce verilen fonksiyonun birinci mertebeden türevini buluruz. farklılaşma kuralları ve kullanarak türev tablosu:

Şimdi birinci dereceden türevin türevini bulalım. Bu, gerekli ikinci dereceden türev olacaktır:

Cevap:

Örnek 2.

Fonksiyonun th-mertebeden türevini bulun

Çözüm.

inci türev için genelleştirilebilecek bir model oluşturmak için, verilen bir fonksiyonun birinci, ikinci, üçüncü ve benzeri mertebelerinin türevlerini sırayla bulacağız.

Birinci dereceden türev şu şekilde bulunur: özel türevi:

Buradaki ifadeye sayının faktöriyeli denir. Bir sayının faktöriyeli, birden bire kadar olan sayıların çarpımına eşittir, yani

İkinci dereceden türev, birinci türevin birinci türevidir, yani

Üçüncü dereceden türev:

Dördüncü türev:

Düzenliliğe dikkat edin: pay, türevin mertebesine eşit olan sayının faktöriyelini içerir ve paydada, kuvvetteki ifade, türevin mertebesinden bir fazladır, yani

Cevap.

Örnek 3.

Noktadaki fonksiyonun üçüncü türevinin değerini bulun.

Çözüm.

Buna göre yüksek mertebeden türevler tablosu, sahibiz:

İncelenen örnekte, yani

Benzer bir sonucun türevleri art arda bularak elde edilebileceğini unutmayın.

Belirli bir noktada üçüncü türev:

Cevap:

Örnek 4.

Bir fonksiyonun ikinci türevini bulun

Çözüm.İlk olarak, birinci türevi bulalım:

İkinci türevi bulmak için birinci türevin ifadesinin türevini tekrar alırız:

Cevap:

Örnek 5.

Eğer bulun

Verilen fonksiyon iki fonksiyonun çarpımı olduğundan, dördüncü dereceden türevi bulmak için Leibniz formülünü kullanmak uygun olacaktır:

Tüm türevleri bulalım ve terimlerin katsayılarını hesaplayalım.

1) Terimlerin katsayılarını hesaplayalım:

2) Fonksiyonun türevlerini bulun:

3) Fonksiyonun türevlerini bulun:

Cevap:

Örnek 6.

Bir fonksiyona y = x 2 cos3x verilir. Üçüncü dereceden türevi bulun.

u = cos3x, v = x 2 olsun ... Sonra Leibniz formülünü kullanarak şunları buluruz:

Bu ifadedeki türevler:

(cos3x) ′ = - 3sin3x,

(cos3x) ′ ′ = (- 3sin3x) ′ = - 9cos3x,

(cos3x) ′ ′ ′ = (- 9cos3x) ′ = 27sin3x,

(x2) ′ = 2x,

(x2) ′ ′ = 2,

(x2) ′ ′ ' = 0.

Bu nedenle, verilen fonksiyonun üçüncü türevi

1 ⋅ 27sin3x ⋅ x2 + 3 ⋅ (−9cos3x) ⋅ 2x + 3 ⋅ (−3sin3x) ⋅ 2 + 1 ⋅ cos3x ⋅ 0

27x2sin3x − 54xcos3x − 18sin3x = (27x2−18) sin3x − 54xcos3x.

Örnek 7.

Türev bul n -. sıra fonksiyonu y = x 2 kosx.

Ayarlayarak Leibniz'in formülünü kullanıyoruzu = cosx, v = x 2 ... Sonra

Serinin kalan terimleri sıfıra eşittir, çünkü(x2) (i) = 0 i> 2 için.

türev n -inci dereceden kosinüs fonksiyonu:

Bu nedenle, fonksiyonumuzun türevi

ÇÖZÜM

Okul, kısaltılmış çarpma formüllerini inceler ve kullanır: iki ifadenin toplamı ve farkının kareleri ve küpleri ve kareler farkını çarpanlara ayırma formülü, iki ifadenin küplerinin toplamı ve farkı. Bu formüllerin genelleştirilmesi, Newton binom formülü ve kuvvetler toplamı ve farkının çarpanlara ayrılması için formüller adı verilen bir formüldür. Bu formüller genellikle çeşitli problemlerin çözümünde kullanılır: bölünebilirliği kanıtlama, kesirleri iptal etme, yaklaşık hesaplamalar. Newton'un iki terimlisiyle yakından ilişkili olan Pascal üçgeninin ilginç özellikleri göz önünde bulundurulur.

Çalışma, konuyla ilgili bilgileri sistematize eder, Newton'un binomunun uygulanmasına ilişkin problemlere örnekler ve derecelerin toplamı ve farkı için formüller verir. Çalışma, bir matematik çemberinin çalışmasında ve matematiğe düşkün olanlar tarafından bağımsız çalışma için kullanılabilir.

KULLANILAN KAYNAKLARIN LİSTESİ

1.Vilenkin N.Ya. Kombinatorik - ed. "Bilim". - M., 1969

2. Nikolsky S.M., Potapov M.K., Reshetnikov N.N., Shevkin A.V. Cebir ve başlangıçlar matematiksel analiz... 10. sınıf: ders kitabı. genel eğitim için. kuruluşlar temel ve ileri düzeyler - M.: Eğitim, 2014. - 431 s.

3. İstatistik, kombinatorik ve olasılık teorisindeki problemlerin çözümü. 7-9 sınıf / yazar - V.N. Studenetskaya. - ed. 2., Rev., - Volgograd: Öğretmen, 2009

4. Savushkina I.A., Khugaev K.D., Tishkin S.B. cebirsel denklemler daha yüksek dereceler / araç setiüniversitelerarası öğrenciler için hazırlık bölümü... - St.Petersburg, 2001.

5. Sharygin I.F. Matematikte seçmeli ders: Problem çözme. öğretici 10 cl için lise. - M.: Eğitim, 1989.

6.Bilim ve Yaşam, Newton'un iki terimi ve Pascal'ın üçgeni[Elektronik kaynak]. - Giriş türü: http://www.nkj.ru/archive/articles/13598/