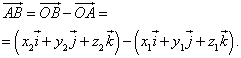In a parallelogram, a point lies on the side , . Express the vector in terms of vectors and .

The solution of the problem

This lesson shows how to express an arbitrary segment through the known vectors in the form of the sides of a parallelogram as a composition of the original vectors. This problem could not have been solved if we did not know in what ratio one of the sides of the parallelogram is divided by a point belonging to the desired segment. Further actions are reduced to determining the beginning and end of the given vectors and the vectors into which the side is divided. All this is necessary in order to use signs correctly when combining vectors. After all, it is necessary to remember the rules of vector addition: the sum of vectors gives a third vector, the beginning of which coincides with the beginning of the first vector, and the end with the end of the second; and the vector subtraction rule: the difference of two vectors is the third vector, the beginning of which coincides with the ends of the second vector, and the end with the end of the first vector. Based on these simple rules, we can get the combination we need.

There will also be tasks for an independent solution, to which you can see the answers.

Vector concept

Before you learn all about vectors and operations on them, tune in to solve a simple problem. There is a vector of your enterprise and a vector of your innovative abilities. The vector of entrepreneurship leads you to Goal 1, and the vector of innovative abilities - to Goal 2. The rules of the game are such that you cannot move in the directions of these two vectors at once and achieve two goals at once. Vectors interact, or, speaking mathematically, some operation is performed on vectors. The result of this operation is the "Result" vector, which leads you to Goal 3.

Now tell me: the result of which operation on the vectors "Enterprise" and "Innovative abilities" is the vector "Result"? If you can't say right away, don't be discouraged. As you study this lesson, you will be able to answer this question.

As we have seen above, the vector necessarily comes from some point A in a straight line to some point B. Consequently, each vector has not only a numerical value - length, but also a physical and geometric - direction. From this the first, simplest definition of a vector is derived. So, a vector is a directed segment going from a point A to the point B. It is marked like this:

And to start different vector operations , we need to get acquainted with one more definition of a vector.

A vector is a kind of representation of a point to be reached from some starting point. For example, a three-dimensional vector is usually written as (x, y, z) . Simply put, these numbers represent how far you have to go in three different directions to get to the point.

Let a vector be given. Wherein x = 3 (right hand points to the right) y = 1 (left hand points forward) z = 5 (under the point there is a ladder leading up). From this data, you will find the point by walking 3 meters in the direction indicated by the right hand, then 1 meter in the direction indicated by the left hand, and then a ladder awaits you and, climbing 5 meters, you will finally find yourself at the end point.

All other terms are refinements of the explanation presented above, necessary for various operations on vectors, that is, for solving practical problems. Let's go through these more rigorous definitions, dwelling on typical vector problems.

Physical examples vector quantities can serve as a bias material point moving in space, the speed and acceleration of this point, as well as the force acting on it.

geometric vector represented in two-dimensional and three-dimensional space in the form directed segment. This is a segment that has a beginning and an end.

If a A is the beginning of the vector, and B is its end, then the vector is denoted by the symbol or a single lowercase letter . In the figure, the end of the vector is indicated by an arrow (Fig. 1)

Length(or module) of a geometric vector is the length of the segment that generates it

The two vectors are called equal , if they can be combined (when the directions coincide) by parallel translation, i.e. if they are parallel, point in the same direction and have equal lengths.

In physics, it is often considered pinned vectors, given by the application point, length, and direction. If the point of application of the vector does not matter, then it can be transferred, keeping the length and direction to any point in space. In this case, the vector is called free. We agree to consider only free vectors.

Linear operations on geometric vectors

Multiply a vector by a number

Vector product per number A vector is called a vector obtained from a vector by stretching (at ) or shrinking (at ) times, and the direction of the vector is preserved if , and reversed if . (Fig. 2)

It follows from the definition that the vectors and = are always located on one or parallel lines. Such vectors are called collinear. (You can also say that these vectors are parallel, but in vector algebra it is customary to say "collinear".) The converse is also true: if the vectors and are collinear, then they are related by the relation

Therefore, equality (1) expresses the condition of collinearness of two vectors.

Vector addition and subtraction

When adding vectors, you need to know that sum vectors and is called a vector , the beginning of which coincides with the beginning of the vector , and the end - with the end of the vector , provided that the beginning of the vector is attached to the end of the vector . (Fig. 3)

This definition can be distributed over any finite number of vectors. Let in space given n free vectors . When adding several vectors, their sum is taken as the closing vector, the beginning of which coincides with the beginning of the first vector, and the end with the end of the last vector. That is, if the beginning of the vector is attached to the end of the vector, and the beginning of the vector to the end of the vector, etc. and, finally, to the end of the vector - the beginning of the vector, then the sum of these vectors is the closing vector , whose beginning coincides with the beginning of the first vector , and whose end coincides with the end of the last vector . (Fig. 4)

The terms are called the components of the vector, and the formulated rule is polygon rule. This polygon may not be flat.

When a vector is multiplied by the number -1, the opposite vector is obtained. The vectors and have the same length and opposite directions. Their sum gives null vector, whose length is zero. The direction of the null vector is not defined.

In vector algebra, there is no need to consider the operation of subtraction separately: to subtract a vector from a vector means to add the opposite vector to the vector, i.e.

Example 1 Simplify the expression:

.

,

that is, vectors can be added and multiplied by numbers in the same way as polynomials (in particular, also problems for simplifying expressions). Usually, the need to simplify linearly similar expressions with vectors arises before calculating the products of vectors.

Example 2 The vectors and serve as diagonals of the parallelogram ABCD (Fig. 4a). Express in terms of and the vectors , , and , which are the sides of this parallelogram.

Solution. The intersection point of the diagonals of a parallelogram bisects each diagonal. The lengths of the vectors required in the condition of the problem are found either as half the sums of the vectors that form a triangle with the desired ones, or as half the differences (depending on the direction of the vector serving as a diagonal), or, as in the latter case, half the sum taken with a minus sign. The result is the vectors required in the condition of the problem:

There is every reason to believe that you now correctly answered the question about the "Enterprise" and "Innovative abilities" vectors at the beginning of this lesson. Correct answer: these vectors are subjected to an addition operation.

Solve problems on vectors on your own, and then look at the solutions

How to find the length of the sum of vectors?

This problem occupies a special place in operations with vectors, as it involves the use of trigonometric properties. Let's say you have a task like the following:

Given the length of vectors and the length of the sum of these vectors . Find the length of the difference of these vectors .

Solutions to this and other similar problems and explanations of how to solve them - in the lesson " Vector addition: the length of the sum of vectors and the cosine theorem ".

And you can check the solution of such problems on Online calculator "Unknown side of a triangle (vector addition and cosine theorem)" .

Where are the products of vectors?

The products of a vector by a vector are not linear operations and are considered separately. And we have lessons "Dot Product of Vectors" and "Vector and Mixed Product of Vectors".

Projection of a vector onto an axis

The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:

As is known, the projection of a point A on the line (plane) is the base of the perpendicular dropped from this point to the line (plane).

Let - an arbitrary vector (Fig. 5), and and - projections of its beginning (points A) and end (dots B) per axle l. (To build the projection of a point A) draw straight through the point A plane perpendicular to the line. The intersection of a line and a plane will determine the required projection.

Component of the vector on the l axis called such a vector lying on this axis, the beginning of which coincides with the projection of the beginning, and the end - with the projection of the end of the vector .

The projection of the vector onto the axis l called a number

,

equal to the length of the component vector on this axis, taken with a plus sign if the direction of the component coincides with the direction of the axis l, and with a minus sign if these directions are opposite.

The main properties of vector projections on the axis:

1. The projections of equal vectors on the same axis are equal to each other.

2. When a vector is multiplied by a number, its projection is multiplied by the same number.

3. The projection of the sum of vectors on any axis is equal to the sum of the projections on the same axis of the terms of the vectors.

4. The projection of a vector onto an axis is equal to the product of the length of the projected vector and the cosine of the angle between the vector and the axis:

.

Solution. Let's project the vectors onto the axis l as defined in the theoretical reference above. From Fig.5a it is obvious that the projection of the sum of vectors is equal to the sum of the projections of vectors. We calculate these projections:

We find the final projection of the sum of vectors:

Relationship of a vector with a rectangular Cartesian coordinate system in space

Acquaintance with rectangular Cartesian coordinate system in space took place in the corresponding lesson, preferably open it in a new window.

In an ordered system of coordinate axes 0xyz axis Ox called x-axis, axis 0y – y-axis, and axis 0z – applicate axis.

with arbitrary point M space tie vector

called radius vector points M and project it onto each of the coordinate axes. Let us denote the values ​​of the corresponding projections:

Numbers x, y, z called coordinates of point M, respectively abscissa, ordinate and applique, and are written as an ordered point of numbers: M(x; y; z)(Fig. 6).

A vector of unit length whose direction coincides with the direction of the axis is called unit vector(or ortom) axes. Denote by

Accordingly, the unit vectors of the coordinate axes Ox, Oy, Oz

Theorem. Any vector can be decomposed into the unit vectors of the coordinate axes:

(2)

Equality (2) is called the expansion of the vector along the coordinate axes. The coefficients of this expansion are the projections of the vector onto the coordinate axes. Thus, the expansion coefficients (2) of the vector along the coordinate axes are the coordinates of the vector.

After choosing in space certain system of coordinates, the vector and the triple of its coordinates uniquely determine each other, so the vector can be written in the form

The vector representations in the form (2) and (3) are identical.

The condition of collinear vectors in coordinates

As we have already noted, vectors are called collinear if they are related by the relation

Let vectors . These vectors are collinear if the coordinates of the vectors are related by the relation

,

that is, the coordinates of the vectors are proportional.

Example 6 Given vectors . Are these vectors collinear?

Solution. Let's find out the ratio of the coordinates of these vectors:

.

The coordinates of the vectors are proportional, therefore, the vectors are collinear, or, what is the same, parallel.

Vector length and direction cosines

Due to the mutual perpendicularity of the coordinate axes, the length of the vector

equal to the length of the diagonal cuboid, built on vectors

and is expressed by the equality

(4)

A vector is completely defined by specifying two points (beginning and end), so the coordinates of the vector can be expressed in terms of the coordinates of these points.

Let the beginning of the vector in the given coordinate system be at the point

and the end is at the point

From equality

Follows that

or in coordinate form

Consequently, the coordinates of the vector are equal to the differences of the coordinates of the same name of the end and beginning of the vector . Formula (4) in this case takes the form

The direction of the vector is determined direction cosines . These are the cosines of the angles that the vector makes with the axes Ox, Oy and Oz. Let's designate these angles respectively α , β and γ . Then the cosines of these angles can be found by the formulas

The direction cosines of a vector are also the coordinates of the vector's vector and thus the vector's vector

.

Considering that the length of the vector vector is equal to one unit, that is,

,

we get the following equality for the direction cosines:

Example 7 Find the length of a vector x = (3; 0; 4).

Solution. The length of the vector is

Example 8 Given points:

Find out if the triangle built on these points is isosceles.

Solution. Using the vector length formula (6), we find the lengths of the sides and find out if there are two of them equal:

Two equal sides have been found, so there is no need to look for the length of the third side, and the given triangle is isosceles.

Example 9 Find the length of a vector and its direction cosines if .

Solution. The vector coordinates are given:

.

The length of the vector is square root from the sum of the squares of the vector coordinates:

.

Finding direction cosines:

Solve the problem on vectors yourself, and then look at the solution

Operations on vectors given in coordinate form

Let two vectors and given by their projections be given:

Let us indicate actions on these vectors.

Finally, I got my hands on an extensive and long-awaited topic analytical geometry. First, a little about this section of higher mathematics…. Surely you now remembered the school geometry course with numerous theorems, their proofs, drawings, etc. What to hide, an unloved and often obscure subject for a significant proportion of students. Analytic geometry, oddly enough, may seem more interesting and accessible. What does the adjective "analytical" mean? Two stamped mathematical phrases immediately come to mind: “graphic method of solution” and “ analytical method solutions". Graphic method, of course, is associated with the construction of graphs, drawings. Analytical same method involves problem solving predominantly through algebraic operations. In this regard, the algorithm for solving almost all problems of analytical geometry is simple and transparent, often it is enough to accurately apply the necessary formulas - and the answer is ready! No, of course, it will not do without drawings at all, besides, for a better understanding of the material, I will try to bring them in excess of the need.

The open course of lessons in geometry does not claim to be theoretical completeness, it is focused on solving practical problems. I will include in my lectures only what, from my point of view, is important in practical terms. If you need a more complete reference on any subsection, I recommend the following quite accessible literature:

1) A thing that, no joke, is familiar to several generations: School textbook on geometry, the authors - L.S. Atanasyan and Company. This school locker room hanger has already withstood 20 (!) reissues, which, of course, is not the limit.

2) Geometry in 2 volumes. The authors L.S. Atanasyan, Bazylev V.T.. This is literature for high school, you will need first volume. Infrequently occurring tasks may fall out of my field of vision, and the tutorial will be of invaluable help.

Both books are free to download online. In addition, you can use my archive with ready-made solutions, which can be found on the page Download higher mathematics examples.

Of the tools, I again offer my own development - software package on analytical geometry, which will greatly simplify life and save a lot of time.

It is assumed that the reader is familiar with basic geometric concepts and figures: point, line, plane, triangle, parallelogram, parallelepiped, cube, etc. It is advisable to remember some theorems, at least the Pythagorean theorem, hello repeaters)

And now we will sequentially consider: the concept of a vector, actions with vectors, vector coordinates. Further I recommend reading the most important article Dot product of vectors, as well as Vector and mixed product of vectors. The local task will not be superfluous - Division of the segment in this regard. Based on the above information, you can equation of a straight line in a plane With the simplest examples of solutions, which will allow learn how to solve problems in geometry. The following articles are also helpful: Equation of a plane in space, Equations of a straight line in space, Basic problems on the line and plane , other sections of analytic geometry. Naturally, standard tasks will be considered along the way.

The concept of a vector. free vector

First, let's repeat the school definition of a vector. Vector called directed a segment for which its beginning and end are indicated:

In this case, the beginning of the segment is the point , the end of the segment is the point . The vector itself is denoted by . Direction is essential, if you rearrange the arrow to the other end of the segment, you get a vector, and this is already completely different vector. It is convenient to identify the concept of a vector with the movement of a physical body: you must admit that entering the doors of an institute or leaving the doors of an institute are completely different things.

It is convenient to consider individual points of a plane, space as the so-called zero vector. Such a vector has the same end and beginning.

!!! Note: Here and below, you can assume that the vectors lie in the same plane or you can assume that they are located in space - the essence of the material presented is valid for both the plane and space.

Designations: Many immediately drew attention to a stick without an arrow in the designation and said that they also put an arrow at the top! That's right, you can write with an arrow: , but admissible and record that I will use later. Why? Apparently, such a habit has developed from practical considerations, my shooters at school and university turned out to be too diverse and shaggy. AT educational literature sometimes they don’t bother with cuneiform at all, but highlight the letters in bold: , thereby implying that this is a vector.

That was the style, and now about the ways of writing vectors:

1) Vectors can be written in two capital Latin letters:
and so on. While the first letter necessarily denotes the start point of the vector, and the second letter denotes the end point of the vector.

2) Vectors are also written in small Latin letters:
In particular, our vector can be redesignated for brevity by a small Latin letter .

Length or module non-zero vector is called the length of the segment. The length of the null vector is zero. Logically.

The length of a vector is denoted by the modulo sign: ,

How to find the length of a vector, we will learn (or repeat, for whom how) a little later.

That was elementary information about the vector, familiar to all schoolchildren. In analytic geometry, the so-called free vector.

If it's quite simple - vector can be drawn from any point:

We used to call such vectors equal (the definition of equal vectors will be given below), but from a purely mathematical point of view, this is the SAME VECTOR or free vector. Why free? Because in the course of solving problems you can “attach” one or another “school” vector to ANY point of the plane or space you need. This is a very cool property! Imagine a directed segment of arbitrary length and direction - it can be "cloned" an infinite number of times and at any point in space, in fact, it exists EVERYWHERE. There is such a student's proverb: Each lecturer in f ** u in the vector. After all, it’s not just a witty rhyme, everything is almost correct - a directed segment can be attached there too. But do not rush to rejoice, students themselves suffer more often =)

So, free vector- this is lots of identical directional segments. school definition vector, given at the beginning of the paragraph: “A directed segment is called a vector ...”, implies specific a directed segment taken from a given set, which is attached to a certain point in the plane or space.

It should be noted that from the point of view of physics, the concept of a free vector is generally incorrect, and the point of application matters. Indeed, a direct blow of the same force on the nose or on the forehead is enough to develop my stupid example entails different consequences. However, not free vectors are also found in the course of vyshmat (do not go there :)).

Actions with vectors. Collinearity of vectors

In the school geometry course, a number of actions and rules with vectors are considered: addition according to the triangle rule, addition according to the parallelogram rule, the rule of the difference of vectors, multiplication of a vector by a number, the scalar product of vectors, etc. As a seed, we repeat two rules that are especially relevant for solving problems of analytical geometry.

Rule of addition of vectors according to the rule of triangles

Consider two arbitrary non-zero vectors and :

It is required to find the sum of these vectors. Due to the fact that all vectors are considered free, we postpone the vector from end vector :

The sum of vectors is the vector . For a better understanding of the rule, it is advisable to invest in it physical meaning: let some body make a path along the vector , and then along the vector . Then the sum of the vectors is the vector of the resulting path starting at the point of departure and ending at the point of arrival. A similar rule is formulated for the sum of any number of vectors. As they say, the body can go its way strongly zigzag, or maybe on autopilot - along the resulting sum vector.

By the way, if the vector is postponed from start vector , then we get the equivalent parallelogram rule addition of vectors.

First, about the collinearity of vectors. The two vectors are called collinear if they lie on the same line or on parallel lines. Roughly speaking, we are talking about parallel vectors. But in relation to them, the adjective "collinear" is always used.

Imagine two collinear vectors. If the arrows of these vectors are directed in the same direction, then such vectors are called co-directional. If the arrows look in different directions, then the vectors will be oppositely directed.

Designations: collinearity of vectors is written with the usual parallelism icon: , while detailing is possible: (vectors are co-directed) or (vectors are directed oppositely).

work of a nonzero vector by a number is a vector whose length is equal to , and the vectors and are co-directed at and oppositely directed at .

The rule for multiplying a vector by a number is easier to understand with a picture:

We understand in more detail:

1) Direction. If the multiplier is negative, then the vector changes direction to the opposite.

2) Length. If the factor is contained within or , then the length of the vector decreases. So, the length of the vector is twice less than the length of the vector . If the modulo multiplier is greater than one, then the length of the vector increases in time.

3) Please note that all vectors are collinear, while one vector is expressed through another, for example, . The reverse is also true: if one vector can be expressed in terms of another, then such vectors are necessarily collinear. In this way: if we multiply a vector by a number, we get collinear(relative to original) vector.

4) The vectors are codirectional. The vectors and are also codirectional. Any vector of the first group is opposite to any vector of the second group.

What vectors are equal?

Two vectors are equal if they are codirectional and have the same length. Note that co-direction implies that the vectors are collinear. The definition will be inaccurate (redundant) if you say: "Two vectors are equal if they are collinear, co-directed and have the same length."

From the point of view of the concept of a free vector, equal vectors are the same vector, which was already discussed in the previous paragraph.

Vector coordinates on the plane and in space

The first point is to consider vectors on a plane. Let's depict the Cartesian rectangular system coordinates and from the origin we set aside single vectors and :

Vectors and orthogonal. Orthogonal = Perpendicular. I recommend slowly getting used to the terms: instead of parallelism and perpendicularity, we use the words respectively collinearity and orthogonality.

Designation: orthogonality of vectors is written with the usual perpendicular sign, for example: .

The considered vectors are called coordinate vectors or orts. These vectors form basis on surface. What is the basis, I think, is intuitively clear to many, more detailed information can be found in the article Linear (non) dependence of vectors. Vector basis.In simple words, the basis and the origin of coordinates define the entire system - this is a kind of foundation on which a full and rich geometric life boils.

Sometimes the constructed basis is called orthonormal basis of the plane: "ortho" - because the coordinate vectors are orthogonal, the adjective "normalized" means unit, i.e. the lengths of the basis vectors are equal to one.

Designation: the basis is usually written in parentheses, inside which in strict order basis vectors are listed, for example: . Coordinate vectors it is forbidden swap places.

Any plane vector the only way expressed as:
, where - numbers, which are called vector coordinates in this basis. But the expression itself called vector decompositionbasis .

Dinner served:

Let's start with the first letter of the alphabet: . The drawing clearly shows that when decomposing the vector in terms of the basis, the ones just considered are used:
1) the rule of multiplication of a vector by a number: and ;
2) addition of vectors according to the triangle rule: .

Now mentally set aside the vector from any other point on the plane. It is quite obvious that his corruption will "relentlessly follow him." Here it is, the freedom of the vector - the vector "carries everything with you." This property, of course, is true for any vector. It's funny that the basis (free) vectors themselves do not have to be set aside from the origin, one can be drawn, for example, at the bottom left, and the other at the top right, and nothing will change from this! True, you don’t need to do this, because the teacher will also show originality and draw you a “pass” in an unexpected place.

Vectors , illustrate exactly the rule for multiplying a vector by a number, the vector is co-directed with the basis vector , the vector is directed opposite to the basis vector . For these vectors, one of the coordinates is equal to zero, it can be meticulously written as follows:


And the basis vectors, by the way, are like this: (in fact, they are expressed through themselves).

And finally: , . By the way, what is vector subtraction, and why didn't I tell you about the subtraction rule? Somewhere in linear algebra, I don't remember where, I noted that subtraction is a special case of addition. So, the expansions of the vectors "de" and "e" are calmly written as a sum: . Follow the drawing to see how well the good old addition of vectors according to the triangle rule works in these situations.

Considered decomposition of the form sometimes called a vector decomposition in the system ort(i.e. in the system of unit vectors). But this is not the only way to write a vector, the following option is common:

Or with an equals sign:

The basis vectors themselves are written as follows: and

That is, the coordinates of the vector are indicated in parentheses. In practical tasks, all three recording options are used.

I doubted whether to speak, but still I will say: vector coordinates cannot be rearranged. Strictly in first place write down the coordinate that corresponds to the unit vector , strictly in second place write down the coordinate that corresponds to the unit vector . Indeed, and are two different vectors.

We figured out the coordinates on the plane. Now consider vectors in three-dimensional space, everything is almost the same here! Only one more coordinate will be added. It is difficult to perform three-dimensional drawings, so I will limit myself to one vector, which for simplicity I will postpone from the origin:

Any 3d space vector the only way expand in an orthonormal basis:
, where are the coordinates of the vector (number) in the given basis.

Example from the picture: . Let's see how the vector action rules work here. First, multiplying a vector by a number: (red arrow), (green arrow) and (magenta arrow). Secondly, here is an example of adding several, in this case three, vectors: . The sum vector starts at the starting point of departure (the beginning of the vector ) and ends up at the final point of arrival (the end of the vector ).

All vectors of three-dimensional space, of course, are also free, try to mentally postpone the vector from any other point, and you will understand that its expansion "remains with it."

Similarly to the plane case, in addition to writing versions with brackets are widely used: either .

If one (or two) coordinate vectors are missing in the expansion, then zeros are put instead. Examples:
vector (meticulously ) – write down ;
vector (meticulously) - write down;
vector (meticulously ) – write down .

Basis vectors are written as follows:

Here, perhaps, is all the minimum theoretical knowledge necessary to solve problems of analytical geometry. Perhaps there are too many terms and definitions, so I recommend dummies to re-read and comprehend this information again. And it will be useful for any reader to refer to the basic lesson from time to time for better assimilation of the material. Collinearity, orthogonality, orthonormal basis, vector decomposition - these and other concepts will be often used in what follows. I note that the materials of the site are not enough to pass a theoretical test, a colloquium on geometry, since I carefully encrypt all theorems (besides without proofs) - to the detriment of the scientific style of presentation, but a plus for your understanding of the subject. In order to receive detailed theoretical information, I ask you to bow to Professor Atanasyan.

Now let's move on to the practical part:

The simplest problems of analytic geometry.
Actions with vectors in coordinates

The tasks that will be considered, it is highly desirable to learn how to solve them fully automatically, and the formulas memorize, don’t even remember it on purpose, they will remember it themselves =) This is very important, because on the simplest elementary examples other analytic geometry problems are based, and it would be annoying to spend extra time eating pawns. You do not need to fasten the top buttons on your shirt, many things are familiar to you from school.

The presentation of the material will follow a parallel course - both for the plane and for space. For the reason that all the formulas ... you will see for yourself.

How to find a vector given two points?

If two points of the plane and are given, then the vector has the following coordinates:

If two points in space and are given, then the vector has the following coordinates:

That is, from the coordinates of the end of the vector you need to subtract the corresponding coordinates vector start.

Exercise: For the same points, write down the formulas for finding the coordinates of the vector. Formulas at the end of the lesson.

Example 1

Given two points in the plane and . Find vector coordinates

Solution: according to the corresponding formula:

Alternatively, one could use next entry:

Aesthetes will decide like this:

Personally, I'm used to the first version of the record.

Answer:

According to the condition, it was not required to build a drawing (which is typical for problems of analytical geometry), but in order to explain some points to dummies, I will not be too lazy:

Must be understood difference between point coordinates and vector coordinates:

Point coordinates are the usual coordinates in a rectangular coordinate system. Set aside points for coordinate plane I think everyone can do it from 5-6 grade. Each point has a strict place on the plane, and they cannot be moved anywhere.

The coordinates of the same vector is its expansion with respect to the basis , in this case . Any vector is free, therefore, if desired or necessary, we can easily postpone it from some other point in the plane. Interestingly, for vectors, you can not build axes at all, a rectangular coordinate system, you only need a basis, in this case, an orthonormal basis of the plane.

The records of point coordinates and vector coordinates seem to be similar: , and sense of coordinates absolutely different, and you should be well aware of this difference. This difference, of course, is also true for space.

Ladies and gentlemen, we fill our hands:

Example 2

a) Given points and . Find vectors and .
b) Points are given and . Find vectors and .
c) Given points and . Find vectors and .
d) Points are given. Find Vectors .

Perhaps enough. These are examples for an independent decision, try not to neglect them, it will pay off ;-). Drawings are not required. Solutions and answers at the end of the lesson.

What is important in solving problems of analytical geometry? It is important to be EXTREMELY CAREFUL in order to avoid the masterful “two plus two equals zero” error. I apologize in advance if I made a mistake =)

How to find the length of a segment?

The length, as already noted, is indicated by the modulus sign.

If two points of the plane and are given, then the length of the segment can be calculated by the formula

If two points in space and are given, then the length of the segment can be calculated by the formula

Note: The formulas will remain correct if the corresponding coordinates are swapped: and , but the first option is more standard

Example 3

Solution: according to the corresponding formula:

Answer:

For clarity, I will make a drawing

Line segment - it's not a vector, and you can't move it anywhere, of course. In addition, if you complete the drawing to scale: 1 unit. \u003d 1 cm (two tetrad cells), then the answer can be checked with a regular ruler by directly measuring the length of the segment.

Yes, the solution is short, but it has a couple more important points I would like to clarify:

First, in the answer we set the dimension: “units”. The condition does not say WHAT it is, millimeters, centimeters, meters or kilometers. Therefore, the general formulation will be a mathematically competent solution: “units” - abbreviated as “units”.

Secondly, let's repeat the school material, which is useful not only for the considered problem:

pay attention to important technical trick – taking the multiplier out from under the root. As a result of the calculations, we got the result and good mathematical style involves taking the factor out from under the root (if possible). The process looks like this in more detail: . Of course, leaving the answer in the form will not be a mistake - but it is definitely a flaw and a weighty argument for nitpicking on the part of the teacher.

Here are other common cases:

Often under the root it turns out enough big number, for example . How to be in such cases? On the calculator, we check if the number is divisible by 4:. Yes, split completely, thus: . Or maybe the number can be divided by 4 again? . In this way: . The last digit of the number is odd, so dividing by 4 for the third time is clearly not possible. Trying to divide by nine: . As a result:
Ready.

Conclusion: if under the root we get a whole number that cannot be extracted, then we try to take out the factor from under the root - on the calculator we check whether the number is divisible by: 4, 9, 16, 25, 36, 49, etc.

In the course of solving various problems, roots are often found, always try to extract factors from under the root in order to avoid a lower score and unnecessary troubles with finalizing your solutions according to the teacher's remark.

Let's repeat the squaring of the roots and other powers at the same time:

The rules for actions with degrees in a general form can be found in a school textbook on algebra, but I think that everything or almost everything is already clear from the examples given.

Task for an independent solution with a segment in space:

Example 4

Given points and . Find the length of the segment.

Solution and answer at the end of the lesson.

How to find the length of a vector?

If a plane vector is given, then its length is calculated by the formula.

If a space vector is given, then its length is calculated by the formula .