DAĞITIM HUKUKU VE ÖZELLİKLERİ

rasgele değerler

Rastgele değişkenler, sınıflandırılmaları ve açıklama yöntemleri.

Rastgele bir değer, deneyimin bir sonucu olarak belirli bir değer alabilen, ancak önceden bilinmeyen bir miktardır. Rastgele bir değişken için, bu nedenle, yalnızca birinin deney sonucunda mutlaka alacağı değerleri belirtebilirsiniz. Bundan sonra, bu değerler rastgele değişkenin olası değerleri olarak adlandırılacaktır. Çünkü rastgele değer Bir deneyin rastgele sonucunu nicel olarak karakterize eder, rastgele bir olayın nicel bir özelliği olarak kabul edilebilir.

Rastgele değişkenler genellikle belirtilir büyük harflerle Latin alfabesi, örneğin X..Y..Z ve olası anlamları karşılık gelen küçük harflerdedir.

Üç tür rastgele değişken vardır:

ayrık; Sürekli; Karışık.

ayrık olası değerlerin sayısı sayılabilir bir küme oluşturan böyle bir rastgele değişken denir. Buna karşılık, elemanları numaralandırılabilen bir kümeye sayılabilir denir. "Ayrık" kelimesi, "süreksiz, ayrı parçalardan oluşan" anlamına gelen Latince discretus'tan gelir.

Örnek 1. Kesikli bir rastgele değişken, bir ntuk partisindeki kusurlu X parçalarının sayısıdır. Gerçekten de, bu rastgele değişkenin olası değerleri, 0'dan n'ye kadar bir dizi tam sayıdır.

Örnek 2. Ayrık bir rastgele değişken, hedefe ilk vuruştan önceki atış sayısıdır. Burada örnek 1'deki gibi olası değerler numaralandırılabilir, ancak sınırlayıcı durumda olası değer sonsuz büyük bir sayıdır.

Sürekli olası değerleri sürekli olarak sayısal eksenin belirli bir aralığını dolduran, bazen bu rastgele değişkenin varlık aralığı olarak adlandırılan rastgele bir değişken olarak adlandırılır. Bu nedenle, herhangi bir sonlu varlık aralığında, sürekli bir rastgele değişkenin olası değerlerinin sayısı sonsuz büyüktür.

Örnek 3. Sürekli bir rastgele değişken, işletmede bir aylık enerji tüketimidir.

Örnek 4. Sürekli bir rastgele değişken, bir altimetre kullanılarak yapılan yükseklik ölçüm hatasıdır. Altimetrenin çalışma prensibinden, hatanın 0 ila 2 m aralığında olduğu bilinsin, bu nedenle, bu rastgele değişkenin varlık aralığı 0 ila 2 m arasındadır.

Rastgele değişkenlerin dağılım yasası.

Rastgele bir değişkenin olası değerleri sayısal eksende belirtilirse ve dağılım yasası kurulursa tamamen verilmiş kabul edilir.

Rastgele bir değişkenin dağılım yasası rastgele bir değişkenin olası değerleri ile karşılık gelen olasılıklar arasındaki ilişkiyi kuran ilişkiye denir.

Rastgele bir değişkenin belirli bir yasaya göre dağıtıldığı veya belirli bir dağıtım yasasına tabi olduğu söylenir. Dağılım yasaları olarak bir dizi olasılık, bir dağılım fonksiyonu, bir olasılık yoğunluğu ve bir karakteristik fonksiyon kullanılır.

Dağılım yasası, rastgele değişkenin tam bir olası tanımını verir. Dağıtım yasasına göre, rastgele bir değişkenin hangi olası değerlerinin daha sık ve hangilerinin - daha az görüneceğini deneyimden önce yargılamak mümkündür.

Kesikli bir rasgele değişken için, dağılım yasası bir tablo şeklinde, analitik olarak (bir formül şeklinde) ve grafik olarak belirtilebilir.

Ayrık bir rastgele değişkenin dağılım yasasını belirlemenin en basit şekli, rastgele değişkenin tüm olası değerlerini ve bunlara karşılık gelen olasılıkları artan sırada listeleyen bir tablodur (matris).

Böyle bir tabloya ayrık bir rastgele değişkenin dağılım serisi denir. bir

Test sonucunda rastgele bir değişken X'in sırasıyla x 1, x 2, ... xn değerlerini alacağı gerçeğinden oluşan X 1, X 2, ..., X n olayları tutarsız ve tek olası (çünkü tablo rasgele değişkenin tüm olası değerlerini listeler), yani. tam bir grup oluşturur. Bu nedenle, olasılıklarının toplamı 1'dir. Böylece, herhangi bir ayrık rastgele değişken için

(Bu birim bir şekilde rastgele değişkenin değerleri arasında dağıtılır, dolayısıyla "dağılım" terimi).

Rastgele değişkenin değerleri apsis ekseni boyunca çizilirse ve bunlara karşılık gelen olasılıklar ordinat ekseni boyunca çizilirse, dağılım serisi grafiksel olarak gösterilebilir. Elde edilen noktaların bağlantısı, bir poligon veya olasılık dağılımının bir poligonu olarak adlandırılan bir çoklu çizgi oluşturur (Şekil 1).

Örnek Piyango çekilişi: 5.000 den değerinde bir araba. üniteler, 250 den değerinde 4 TV. birim, 200 den değerinde 5 video kaydedici. birimler 7 gün boyunca toplam 1000 bilet satılmıştır. birimler Bir bilet alan piyango katılımcısının elde ettiği net kazancın dağıtım kanununu hazırlayın.

Çözüm... Rastgele değişken X'in olası değerleri - bilet başına net kazanç - 0-7 = -7 den. birimler (bilet kazanılmazsa), 200-7 = 193, 250-7 = 243, 5000-7 = 4993 den. birimler (bilet sırasıyla bir VCR, TV veya araba kazançlarını içeriyorsa). 1000 biletten kazanan olmayanların sayısının 990 olduğu ve belirtilen kazançların sırasıyla 5, 4 ve 1 olduğu göz önüne alındığında ve klasik olasılık tanımını kullanarak elde ederiz.

"Rastgele değişkenler" konusundaki problem çözme örnekleri.

Görev 1 ... Piyangoda verilen 100 bilet var. 50 USD'lik bir galibiyet oynandı. ve her biri 10 dolarlık on galibiyet. X değerinin dağıtım yasasını bulun - olası kazancın maliyeti.

Çözüm. X'in olası değerleri: x 1 = 0; x 2 = 10 ve x 3 = 50. 89 “boş” bilet olduğu için p 1 = 0.89, kazanma olasılığı 10 dolar. (10 bilet) - p 2 = 0.10 ve 50 USD kazanmak için. - P 3 = 0.01. Böylece:

Kontrolü kolay:.

Görev 2. Alıcının ürünün reklamını önceden okumuş olma olasılığı 0.6'dır (p = 0.6). Reklamın kalitesinin seçici bir kontrolü, reklamı önceden inceleyen ilk alıcıdan önce alıcılarla görüşülerek gerçekleştirilir. Ankete katılan alıcıların sayısının bir dizi dağılımını oluşturun.

Çözüm. Problemin durumuna göre p = 0.6. Nerede: q = 1 -p = 0.4. Bu değerleri değiştirerek şunu elde ederiz: ve bir dağıtım serisi oluşturun:

Görev 3. Bir bilgisayar birbirinden bağımsız çalışan üç öğeden oluşur: bir sistem birimi, bir monitör ve bir klavye. Voltajda tek bir keskin artışla, her bir elemanın arıza olasılığı 0,1'dir. Bernoulli dağılımına dayanarak, ağdaki bir voltaj dalgalanması sırasında başarısız olan elemanların sayısı için dağıtım yasasını hazırlayın.

Çözüm. Düşünmek Bernoulli dağılımı(veya binom): içinde olma olasılığı n deneme olayı A tam olarak görünecek k bir Zamanlar: 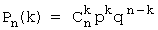, veya:

V Soruna geri dönelim.

Olası X değerleri (arıza sayısı):

x 0 = 0 - öğelerin hiçbiri başarısız oldu;

x 1 = 1 - bir elemanın arızası;

x 2 = 2 - iki elemanın arızası;

x 3 = 3 - tüm elemanların başarısızlığı.

Koşulla, p = 0.1 olduğundan, o zaman q = 1 - p = 0.9. Bernoulli formülünü kullanarak,

, ,

, .

Kontrol: .

Bu nedenle, aranan dağıtım yasası:

4. sorun... 5.000 mermi üretti. Bir kartuşun arızalı olma olasılığı 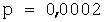... Tüm partide tam olarak 3 kusurlu kartuş olma olasılığı nedir?

Çözüm. uygulanabilir Poisson Dağılımı: Bu dağılım, çok büyük bir

Her birinde A olayının olasılığının çok küçük olduğu deneme sayısı (kitlesel denemeler), A olayı k kez gerçekleşecek: , nerede .

Burada n = 5000, p = 0.0002, k = 3. Gerekli olasılığı buluruz: .

Sorun 5... Vuruş olasılığı p ile ilk vuruşa kadar çekim yaparken = 0.6 Ateş ederken, vuruşun üçüncü atışta meydana gelme olasılığını bulmanız gerekir.

Çözüm. Geometrik bir dağılım uygulayalım: her birinde A olayının p olma olasılığına (ve q = 1 - p olmama) sahip olduğu bağımsız testler gerçekleştirilsin. Denemeler, A olayı biter bitmez sona erer.

Bu koşullar altında, k'inci testte A olayının meydana gelme olasılığı şu formülle belirlenir: Burada p = 0.6; q = 1 - 0.6 = 0.4; k = 3. Bu nedenle,.

6. sorun... Bir rasgele değişken X'in dağılım yasası verilsin:

Bulmak beklenen değer.

Çözüm. ...

Matematiksel beklentinin olasılıksal anlamının, rastgele bir değişkenin ortalama değeri olduğuna dikkat edin.

7. Sorun... Aşağıdaki dağılım yasasına sahip bir X rastgele değişkeninin varyansını bulun:

Çözüm. Burada .

X miktarının karesinin dağılım yasası 2 :

İstenen varyans:.

Dağılım, rastgele bir değişkenin matematiksel beklentisinden sapma (dağılım) ölçüsünü karakterize eder.

8. Sorun... Dağılım tarafından bir rastgele değişken verilsin:

Sayısal özelliklerini bulunuz.

Çözüm: m, m 2 ,

m 2 , m.

Rastgele bir X değişkeni hakkında şunlar söylenebilir - matematiksel beklentisi 13.04 m'lik bir varyansla 6.4 m'dir. 2 , veya - matematiksel beklentisi m sapma ile 6.4 m'dir İkinci formülasyon açıkça daha açıktır.

Görev 9. rastgele değer x dağıtım fonksiyonu tarafından verilen:
.

Test sonucunda X değerinin aralıktaki değeri alma olasılığını bulun. .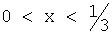

Çözüm. X'in belirli bir aralıktan bir değer alma olasılığı, bu aralıktaki integral fonksiyonunun artışına eşittir, yani. ... Bizim durumumuzda ve bu nedenle

.

Görev 10. Ayrık rassal değişken x dağıtım kanunu tarafından verilen:

dağıtım işlevini bulun F (x ) ve grafiğini oluşturun.

Çözüm. Dağıtım fonksiyonundan beri,

için , sonra

;

;

;

;

İlgili grafik:

Sorun 11. Sürekli rastgele değişken x diferansiyel dağılım fonksiyonu tarafından verilen: .

çarpma olasılığını bulunuz X aralığında

Çözüm. Bunun üstel dağılım yasasının özel bir durumu olduğuna dikkat edin.

Formülü kullanalım: .

Görev 12. Dağılım yasası tarafından verilen ayrık bir rastgele değişken X'in sayısal özelliklerini bulun:

Bilindiği üzere, rastgele değişken duruma göre belirli değerler alabilen bir değişken denir. Rastgele değişkenler, Latin alfabesinin büyük harfleriyle (X, Y, Z) ve değerleriyle - karşılık gelen küçük harflerle (x, y, z) belirtilir. Rastgele değişkenler süreksiz (ayrık) ve sürekli olarak ikiye ayrılır.

Ayrık rassal değişken belirli sıfır olmayan olasılıklarla yalnızca sonlu veya sonsuz (sayılabilir) bir değerler kümesi alan rastgele bir değişkendir.

Ayrık bir rastgele değişkenin dağılım yasası rastgele bir değişkenin değerlerini karşılık gelen olasılıklarla birleştiren bir fonksiyona denir. Dağıtım yasası aşağıdaki yollardan biriyle belirlenebilir.

1 . Dağıtım yasası tablo ile verilebilir:

burada λ> 0, k = 0, 1, 2,….

v)üzerinden dağıtım fonksiyonu F (x) , bu, x'in her değeri için, bir rastgele değişken X'in x'ten daha küçük bir değer alma olasılığını belirler, yani. F(x) = P(X< x).

F (x) fonksiyonunun özellikleri

3 . Dağıtım yasası grafiksel olarak ayarlanabilir - çokgen (çokgen) dağılımı (görev 3'e bakın).

Bazı sorunları çözmek için dağıtım yasasını bilmenin gerekli olmadığını unutmayın. Bazı durumlarda dağıtım kanununun en önemli özelliklerini yansıtan bir veya birkaç sayıyı bilmek yeterlidir. Rastgele bir değişkenin "ortalama değeri" anlamına gelen bir sayı veya bir rastgele değişkenin ortalama değerinden ortalama sapmasını gösteren bir sayı olabilir. Bu tür sayılara rastgele bir değişkenin sayısal özellikleri denir.

Ayrık bir rastgele değişkenin temel sayısal özellikleri :

• matematiksel beklenti (ortalama) ayrık rastgele değişken M (X) = Σ x ben p ben.
  Binom dağılımı için M (X) = np, Poisson dağılımı için M (X) = λ
• Dağılım Ayrık rassal değişken D (X) = M2 veya D (X) = M (X 2) - 2... X – M (X) farkına rastgele bir değişkenin matematiksel beklentisinden sapması denir.
  Binom dağılımı için D (X) = npq, Poisson dağılımı için D (X) = λ
• Standart sapma (standart sapma) σ (X) = √D (X).

"Ayrık bir rastgele değişkenin dağılım yasası" konusundaki problem çözme örnekleri

Amaç 1.

1000 piyango bileti düzenlendi: 5 tanesi 500 ruble kazandı, 10 tanesi 100 ruble kazandı, 20 tanesi 50 ruble kazandı, 50 tanesi 10 ruble kazandı. Bir rasgele değişken X'in olasılık dağılımı yasasını belirleyin - bilet başına bir getiri.

Çözüm. Problemin durumuna göre, X rastgele değişkeninin şu değerleri mümkündür: 0, 10, 50, 100 ve 500.

Kazanmayan biletlerin sayısı 1000 - (5 + 10 + 20 + 50) = 915, ardından P (X = 0) = 915/1000 = 0.915.

Benzer şekilde, diğer tüm olasılıkları buluruz: P (X = 0) = 50/1000 = 0.05, P (X = 50) = 20/1000 = 0.02, P (X = 100) = 10/1000 = 0.01 , P (X = 500) = 5/1000 = 0,005. Ortaya çıkan yasayı bir tablo şeklinde temsil ediyoruz:

X değerinin matematiksel beklentisini bulalım: M (X) = 1 * 1/6 + 2 * 1/6 + 3 * 1/6 + 4 * 1/6 + 5 * 1/6 + 6 * 1/6 = (1+ 2 + 3 + 4 + 5 + 6) / 6 = 21/6 = 3.5

Amaç 3.

Cihaz, birbirinden bağımsız çalışan üç elemandan oluşur. Bir deneyde her bir elemanın başarısız olma olasılığı 0,1'dir. Bir deneyde başarısız olan öğelerin sayısı için bir dağıtım yasası hazırlayın, bir dağıtım çokgeni oluşturun. F (x) dağılım fonksiyonunu bulun ve grafiğini çizin. Kesikli bir rastgele değişkenin matematiksel beklentisini, varyansını ve standart sapmasını bulun.

Çözüm. 1. Kesikli bir rastgele değişken X = (bir deneydeki başarısız öğelerin sayısı) aşağıdaki olası değerlere sahiptir: x 1 = 0 (cihazın öğelerinden hiçbiri başarısız), x 2 = 1 (bir öğe başarısız), x 3 = 2 ( iki öğe başarısız oldu ) ve x 4 = 3 (üç öğe başarısız oldu).

Elemanların arızaları birbirinden bağımsızdır, her elemanın arızalanma olasılıkları birbirine eşittir, dolayısıyla uygulanabilirdir. Bernoulli formülü ... n = 3, p = 0.1, q = 1-p = 0.9 koşuluna göre, değerlerin olasılıklarını belirleriz:
P 3 (0) = C 3 0 p 0 q 3-0 = q 3 = 0.9 3 = 0.729;
P 3 (1) = C 3 1 p 1 q 3-1 = 3 * 0.1 * 0.9 2 = 0.243;
P 3 (2) = C 3 2 p 2 q 3-2 = 3 * 0.1 2 * 0.9 = 0.027;
P 3 (3) = C 3 3 p 3 q 3-3 = p 3 = 0.1 3 = 0.001;
Kontrol edin: ∑p i = 0.729 + 0.243 + 0.027 + 0.001 = 1.

Böylece, X için aranan binom dağılım yasası şu şekildedir:

Apsis ekseninde, x i'nin olası değerlerini ve ordinat ekseninde - karşılık gelen olasılıklar p i'yi ortaya koyuyoruz. M 1 (0; 0.729), M 2 (1; 0.243), M 3 (2; 0.027), M 4 (3; 0.001) noktalarını oluşturalım. Bu noktaları doğru parçalarıyla birleştirerek istenen dağıtım poligonunu elde ederiz.

3. F (x) = P (X) dağılım fonksiyonunu bulalım.

Fonksiyon grafiği F (x)

4. Binom dağılımı X için:
- matematiksel beklenti M (X) = np = 3 * 0.1 = 0.3;
- varyans D (X) = npq = 3 * 0.1 * 0.9 = 0.27;
- standart sapma σ (X) = √D (X) = √0.27 ≈ 0.52.

rastgele bir değer Aynı koşullar altında yapılan testler sonucunda, hesaba katılmayan rastgele faktörlere bağlı olarak, genel olarak farklı değerler alan bir miktar denir. Rastgele değişkenlere örnekler: zarın üzerine düşen puanların sayısı, partideki kusurlu öğelerin sayısı, merminin hedeften sapma noktası, cihazın çalışma süresi, vb. Ayrık ve sürekli arasında ayrım yapın rastgele değişkenler. ayrık Olası değerleri sayılabilir bir küme, sonlu veya sonsuz (yani, öğeleri numaralandırılabilen bir küme) oluşturan rastgele bir değişken denir.

Sürekli Olası değerleri sürekli olarak sayısal eksenin bazı sonlu veya sonsuz aralığını dolduran rastgele bir değişken olarak adlandırılır. Sürekli bir rastgele değişkenin değer sayısı her zaman sonsuzdur.

Rastgele değişkenler, Latin alfabesinin sonundaki büyük harflerle gösterilecektir: x, Y,. ; rastgele bir değişkenin değerleri - küçük harflerle: X, y,... ... Böylece, x Rastgele bir değişkenin tüm olası değerleri kümesini belirtir ve X - Bazı özel anlamı.

dağıtım yasası Kesikli bir rastgele değişken, bir rastgele değişkenin olası değerleri ile olasılıkları arasında herhangi bir biçimde verilen bir yazışmadır.

Rastgele değişkenin olası değerlerine izin verin x var. Test sonucunda rastgele değişken bu değerlerden birini yani; Tam bir ikili uyumsuz olay grubundan bir olay meydana gelecektir.

Bu olayların olasılıkları da bilinsin:

Rastgele bir değişkenin dağılım yasası x adı verilen bir tablo şeklinde yazılabilir. Yakın dağıtım Ayrık rassal değişken:

Rastgele değişkenler. Ayrık rassal değişken.
Beklenen değer

İkinci bölüm olasılık teorisi adanmış rastgele değişkenler Konuyla ilgili her makalede kelimenin tam anlamıyla bize görünmez bir şekilde eşlik eden . Ve ne olduğunu açıkça formüle etmenin zamanı geldi:

Rastgele arandı büyüklük, testin bir sonucu olarak alacak bir ve sadece bir rastgele faktörlere bağlı olan ve önceden tahmin edilemeyen sayısal bir değer.

Rastgele değişkenler genellikle belirtmek karşısında * , ve anlamları, örneğin, karşılık gelen küçük harfli aboneliklerdedir.

* Bazen Yunanca harflerin yanı sıra kullanılır

bir örnekle karşılaştık olasılık teorisindeki ilk ders, burada aslında aşağıdaki rastgele değişkeni düşündük:

- zar atıldıktan sonra düşecek puan sayısı.

Bu testin sonucunda, biricik hangisinin tahmin edilmeyeceği kenar (hileler dikkate alınmaz); bu durumda rastgele değişken aşağıdaki değerlerden birini alabilir:

- 10 yenidoğan arasındaki erkek çocuk sayısı.

Bu sayının önceden bilinmediği oldukça açıktır ve doğacak sonraki on çocukta şunlar olabilir:

Veya erkekler - bir ve sadece bir listelenen seçeneklerden.

Ve formda kalmak için biraz beden eğitimi:

- uzun atlama aralığı (bazı birimlerde).

Sporun ustası bile onu tahmin edemez 🙂

Ancak, hipoteziniz?

En kısa zamanda gerçek sayılar kümesi sonsuz ise, rastgele değişken alabilir sonsuz sayıda belirli bir aralıktaki değerler. Ve bu, önceki örneklerden temel farkıdır.

Böylece, rastgele değişkenleri 2 büyük gruba ayırmanız tavsiye edilir:

1) Ayrık (süreksiz) rastgele değişken - ayrı ayrı alınan, izole edilmiş değerleri alır. Bu değerlerin sayısı kesinlikle veya sonsuz ama sayılabilir.

… Anlaşılmaz terimler mi çıktı? Acilen tekrarlıyoruz cebirin temelleri!

2) Sürekli rastgele değişken - alır Tümü bazı sonlu veya sonsuz aralıktaki sayısal değerler.

Not : eğitim literatüründe, DSV ve NSV kısaltmaları popülerdir

Önce, kesikli bir rastgele değişkeni analiz edelim, sonra - sürekli.

Ayrık bir rastgele değişkenin dağılım yasası

- o uygunluk bu miktarın olası değerleri ile olasılıkları arasında. Çoğu zaman, yasa bir tabloda yazılır:

Oldukça sık terim sıra dağıtım ama bazı durumlarda kulağa belirsiz geliyor ve bu nedenle "yasaya" bağlı kalacağım.

Ve şimdi çok önemli nokta: rastgele değişkenden beri mutlaka kabul edecek anlamlardan biri, ardından ilgili olaylar formu tam grup ve bunların oluşma olasılıklarının toplamı bire eşittir:

veya, eğer yazıldıysa daraltılmış durumda:

Örneğin, bir zara düşen noktaların olasılık dağılımı yasası aşağıdaki gibidir:

Ayrık bir rastgele değişkenin yalnızca "iyi" tamsayı değerleri alabileceği izlenimi altında olabilirsiniz. İllüzyonu ortadan kaldıralım - herhangi bir şey olabilirler:

Bazı oyunlarda aşağıdaki kazanan dağıtım yasası vardır:

... muhtemelen uzun zamandır bu tür görevlerin hayalini kurmuşsunuzdur 🙂 Size bir sır vereceğim - ben de. Özellikle üzerinde çalışmayı bitirdikten sonra alan teorisi.

Çözüm: rasgele bir değişken üç değerden yalnızca birini alabildiğinden, karşılık gelen olaylar tam grup, bu, olasılıklarının toplamının bire eşit olduğu anlamına gelir:

"Partizan"ı ifşa edeceğiz:

- böylece, geleneksel birimleri kazanma olasılığı 0,4'tür.

Kontrol: ikna olmak için gerekli olan şey.

Yanıt vermek:

Dağıtım yasasının bağımsız olarak hazırlanması gerektiğinde nadir görülen bir durum değildir. Bunu yapmak için kullanın olasılığın klasik tanımı, olay olasılıkları için çarpma / toplama teoremleri ve diğer cipsler tervera:

Kutu, 12'si kazanan, 2'si her biri 1000 ruble ve geri kalanı - her biri 100 ruble olan 50 piyango bileti içerir. Rastgele bir değişkenin dağıtım yasasını çizin - kutudan rastgele bir bilet alınırsa ödemenin boyutu.

Çözüm: fark ettiğiniz gibi, rastgele bir değişkenin değerlerini sıralamak gelenekseldir. artan düzen... Bu nedenle, en küçük kazançlarla, yani ruble ile başlıyoruz.

Toplamda 50 - 12 = 38 böyle bilet var ve klasik tanım:
- Rastgele çekilen bir biletin kaybedilmiş olma olasılığı.

Davaların geri kalanı basit. Ruble kazanma olasılığı:

Ve için :

Kontrol edin: - ve bu, bu tür görevlerin özellikle hoş bir anı!

Yanıt vermek: ödemenin gerekli dağılımı:

Bağımsız çözüm için bir sonraki görev:

Atıcının hedefi vurma olasılığı. Rastgele bir değişkenin dağılım yasasını çizin - 2 atıştan sonraki isabet sayısı.

...Onu özlediğini biliyordum 🙂 Hatırla çarpma ve toplama teoremleri... Çözüm ve cevap dersin sonunda.

Dağılım kanunu bir rastgele değişkeni tamamen tanımlar, ancak pratikte sadece bir kısmını bilmek faydalıdır (ve bazen daha faydalıdır). sayısal özellikler .

Ayrık bir rastgele değişkenin matematiksel beklentisi

Basit bir ifadeyle, ortalama beklenen değer testlerin çoklu tekrarı ile. Rastgele değişken sırasıyla olasılıklı değerler alsın. O zaman belirli bir rastgele değişkenin matematiksel beklentisi ürünlerin toplamı tüm değerlerinden ilgili olasılıklara:

veya daraltılmış:

Örneğin, rastgele bir değişkenin matematiksel beklentisini - bir zarın üzerine düşen puan sayısını hesaplayalım:

Elde edilen sonucun olasılıksal anlamı nedir? Zarı birçok kez atarsanız, kastetmek düşen puanlar 3.5'e yakın olacak - ve ne kadar çok test yapılırsa o kadar yakın olur. Aslında, bu etki hakkında derste ayrıntılı olarak bahsettim. istatistiksel olasılık.

Şimdi varsayımsal oyunumuzu hatırlayalım:

Soru ortaya çıkıyor: Bu oyunu oynamak hiç karlı mı? … Kimin nasıl bir izlenimi var? Yani sonuçta "hazır" ve söylemeyeceksin! Ancak bu soru, beklenen değeri hesaplayarak kolayca cevaplanabilir, aslında - ağırlıklı ortalama kazanma olasılıklarına göre:

Böylece, bu oyunun matematiksel beklentisi kaybetmek.

İzlenimlere güvenmeyin - sayılara güvenin!

Evet, burada arka arkaya 10 hatta 20-30 kez kazanabilirsiniz, ancak uzun vadede kaçınılmaz olarak mahvoluruz. Ve bu tür oyunları oynamanızı tavsiye etmem 🙂 Eh, belki sadece eğlence için.

Yukarıdakilerin hepsinden, matematiksel beklentinin artık bir RANDOM değeri olmadığı sonucu çıkar.

Kendi kendine çalışma için yaratıcı ödev:

Bay X, Avrupa ruletini aşağıdaki sisteme göre oynar: "kırmızı" üzerine sürekli olarak 100 ruble bahis yapar. Rastgele bir değişkenin dağıtım yasasını - kazancını çizin. Bir galibiyetin matematiksel beklentisini hesaplayın ve bunu en yakın kopek'e yuvarlayın. kaç ortalama oyuncu her yüz bahiste kaybeder mi?

referans : Avrupa ruleti 18 kırmızı, 18 siyah ve 1 yeşil sektör ("sıfır") içerir. "Kırmızı" isabet durumunda, oyuncuya iki katı bahis ödenir, aksi takdirde kumarhanenin gelirine gider

Kendi olasılık tablolarınızı oluşturabileceğiniz başka birçok rulet oyun sistemi vardır. Ancak bu, herhangi bir dağıtım kuralına ve tabloya ihtiyacımız olmadığında, oyuncunun matematiksel beklentisinin tam olarak aynı olacağı kesin olarak belirlenmiştir. Sistemden sisteme sadece değişir dağılım, dersin 2. bölümünde öğreneceğiz.

Ama önce, parmaklarınızı hesap makinesi tuşlarına uzatmanız faydalı olacaktır:

Rastgele bir değişken, kendi olasılık dağılım yasasıyla verilir:

Bunun bilinip bilinmediğini bulun. Buna bir bak.

Sonra çalışmaya devam ederiz ayrık bir rastgele değişkenin varyansı ve mümkünse, ŞU ANDA!!- konunun başlığını kaybetmemek için.

Çözümler ve Cevaplar:

Örnek 3. Çözüm: koşula göre - hedefi vurma olasılığı. O zamanlar:
- ıskalama olasılığı.

Oluşturalım - iki atış için isabet dağılımı yasası:

- tek bir vuruş yok. İle bağımsız olayların olasılıkları için çarpma teoremi:

- bir vuruş. İle bağımsız olayların tutarsız ve çarpma olasılıklarının eklenmesi teoremleri:

- iki vuruş. Bağımsız olayların olasılıkları için çarpma teoremi ile:

Kontrol: 0,09 + 0,42 + 0,49 = 1

Yanıt vermek :

Not : notasyonu kullanmak mümkündü - önemli değil.

Örnek 4. Çözüm: oyuncu, 37 vakanın 18'inde 100 ruble kazanır ve bu nedenle kazancının dağıtım yasası aşağıdaki gibidir:

Matematiksel beklentiyi hesaplayalım:

Böylece, her yüz bahis için oyuncu ortalama 2,7 ruble kaybeder.

Örnek 5. Çözüm: matematiksel beklentinin tanımı gereği:

parçaları değiştirelim ve basitleştirelim:

Böylece:

Hadi kontrol edelim:

, doğrulanması gerekiyordu.

Yanıt vermek :

(Ana sayfaya git)

İntihal içermeyen kaliteli çalışma - Zaochnik.com

www.mathprofi.ru

Ayrık rastgele değişkenler

rastgele bir değer Her test sonucunda rastgele nedenlere bağlı olarak önceden bilinmeyen bir değer alan değişkene değişken denir. Rastgele değişkenler büyük Latin harfleriyle gösterilir: $ X, \ Y, \ Z, \ \ dots $ Türlerine göre, rastgele değişkenler şunlar olabilir: ayrık ve sürekli.

Ayrık rassal değişken değerleri sayılabilir, yani sonlu veya sayılabilirden fazla olamayan rastgele bir değişkendir. Sayılabilirlik, rastgele bir değişkenin değerlerinin numaralandırılabileceği anlamına gelir.

örnek 1 ... Kesikli rastgele değişkenlere bazı örnekler:

a) $ n $ atışları ile hedefe isabet sayısı, burada olası değerler $ 0, \ 1, \ \ dots, \ n $'dır.

b) Madeni para havaya atıldığında düşen arma sayısı, burada olası değerler $ 0, \ 1, \ \ dots, \ n $'dır.

c) Gemiye gelen gemi sayısı (sayılabilir değerler dizisi).

d) PBX'e gelen çağrıların sayısı (sayılabilir değerler kümesi).

1. Kesikli bir rastgele değişken için olasılık dağılımı yasası.

Kesikli rastgele değişken $ X $, $ x_1, \ dots, \ x_n $, olasılıkları $ p \ left (x_1 \ right), \ \ dots, \ p \ left (x_n \ right) $ değerlerini alabilir. Bu değerler ile olasılıkları arasındaki yazışmaya denir. ayrık bir rastgele değişkenin dağılım yasası... Kural olarak, bu yazışma, ilk satırda $ x_1, \ dots, \ x_n $ değerlerinin belirtildiği ve ikinci satırda $ p_1, \ dots, \ p_n $ olasılıklarının belirtildiği bir tablo kullanılarak ayarlanır. bu değerlere karşılık gelir.

$ \ başlangıç
\ çizgi
X_i & x_1 & x_2 & \ noktalar & x_n \\
\ çizgi
p_i & p_1 & p_2 & \ noktalar & p_n \\
\ çizgi
\ bitiş $

Örnek 2 ... Rastgele değişken $ X $, bir zar atılırken düşen puanların sayısı olsun. Böyle bir rastgele değişken $ X $, şu değerleri alabilir: $ 1, \ 2, \ 3, \ 4, \ 5, \ 6 $. Tüm bu değerlerin olasılıkları 1/6 $ 'dır. Ardından $ X $ rasgele değişkeni için olasılık dağılım yasası:

$ \ başlangıç
\ çizgi
1 & 2 & 3 & 4 & 5 & 6 \\
\ çizgi
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\ çizgi
\ bitiş $

Yorum Yap... Ayrık bir rastgele değişkenin dağılım yasasında $ X $ olaylar $ 1, \ 2, \ \ dots, \ 6 $ tam bir olay grubu oluşturduğundan, olasılıkların toplamı bire eşit olmalıdır, yani, $ \ toplam

2. Kesikli bir rastgele değişkenin matematiksel beklentisi.

Rastgele bir değişkenin matematiksel beklentisi"merkezi" anlamını belirler. Kesikli bir rastgele değişken için, beklenti, karşılık gelen $ p_1, \ dots, \ p_n $ olasılıkları ile $ x_1, \ dots, \ x_n $ değerlerinin ürünlerinin toplamı olarak hesaplanır, yani: $ M \ sol (X \ sağ) = \ toplam ^ n_ $. İngiliz dili literatüründe farklı bir gösterim kullanılır, $ E \ left (X \ right) $.

Matematiksel beklenti özellikleri$ M \ sol (X \ sağ) $:

1. $ M \ left (X \ right) $, $ X $ rastgele değişkeninin en küçük ve en büyük değerleri arasına alınır.
2. Bir sabitin matematiksel beklentisi, sabitin kendisine eşittir, yani. $ M \ sol (C \ sağ) = C $.
3. Sabit faktör matematiksel beklenti işaretinin dışında alınabilir: $ M \ sol (CX \ sağ) = CM \ sol (X \ sağ) $.
4. Rastgele değişkenlerin toplamının matematiksel beklentisi, matematiksel beklentilerinin toplamına eşittir: $ M \ sol (X + Y \ sağ) = M \ sol (X \ sağ) + M \ sol (Y \ sağ) $.
5. Bağımsız rastgele değişkenlerin çarpımının matematiksel beklentisi, matematiksel beklentilerinin çarpımına eşittir: $ M \ sol (XY \ sağ) = M \ sol (X \ sağ) M \ sol (Y \ sağ) $.

Örnek 3 ... $ X $ rasgele değişkeninin matematiksel beklentisini örnek $ 2 $'dan bulalım.

$ M \ left (X \ right) $ 'ın $ X $ rastgele değişkeninin en küçük (1 $) ve en büyük (6 $) değerleri arasına alındığını fark edebiliriz.

Örnek 4 ... $ X $ rastgele değişkeninin matematiksel beklentisinin $ M \ left (X \ right) = 2 $'a eşit olduğu bilinmektedir. $ 3X + 5 $ rastgele değişkeninin matematiksel beklentisini bulun.

Yukarıdaki özellikleri kullanarak, $ M \ left (3X + 5 \ right) = M \ left (3X \ right) + M \ left (5 \ sağ) = 3M \ left (X \ right) + 5 = 3 \ elde ederiz. cdot 2 + 5 = 11 $.

Örnek 5 ... $ X $ rastgele değişkeninin matematiksel beklentisinin $ M \ left (X \ right) = 4 $'a eşit olduğu bilinmektedir. $ 2X-9 $ rasgele değişkeninin matematiksel beklentisini bulun.

Yukarıdaki özellikleri kullanarak $ M \ left (2X-9 \ right) = M \ left (2X \ right) -M \ left (9 \ sağ) = 2M \ left (X \ right) -9 = 2 \ cdot elde ederiz. 4 -9 = -1 $.

3. Kesikli bir rastgele değişkenin dağılımı.

Eşit matematiksel beklentilere sahip rastgele değişkenlerin olası değerleri, ortalama değerleri etrafında farklı şekillerde dağılabilir. Örneğin, iki öğrenci grubunda olasılık teorisindeki sınavın ortalama puanı 4 çıktı, ancak bir grupta herkes iyi çıktı ve diğer grupta - sadece C ve A. Bu nedenle, bir rastgele değişkenin değerlerinin matematiksel beklentisi etrafında yayılmasını gösterecek böyle bir sayısal özelliğe ihtiyaç vardır. Bu özellik varyanstır.

Ayrık bir rastgele değişkenin dağılımı$ X $ şuna eşittir:

İngiliz literatüründe $ V \ left (X \ right), \ Var \ left (X \ right) $ gösterimi kullanılır. Çoğu zaman $ D \ left (X \ right) $ varyansı $ D \ left (X \ right) = \ toplam ^ n_ formülüyle hesaplanır. —^2$.

Dağılım özellikleri$ D \ sol (X \ sağ) $:

1. Varyans her zaman sıfırdan büyük veya sıfıra eşittir, yani. $ D \ sol (X \ sağ) \ ge 0 $.
2. Sabitin varyansı sıfıra eşittir, yani. $ D \ sol (C \ sağ) = 0 $.
3. Sabit faktör, karesi alınmış olması koşuluyla varyans işaretinden çıkarılabilir, yani. $ D \ sol (CX \ sağ) = C ^ 2B \ sol (X \ sağ) $.
4. Bağımsız rastgele değişkenlerin toplamının varyansı, varyanslarının toplamına eşittir, yani. $ D \ sol (X + Y \ sağ) = D \ sol (X \ sağ) + D \ sol (Y \ sağ) $.
5. Bağımsız rastgele değişkenlerin farkının varyansı, varyanslarının toplamına eşittir, yani. $ D \ sol (X-Y \ sağ) = D \ sol (X \ sağ) + D \ sol (Y \ sağ) $.

Örnek 6 ... Örnek $ 2 $'dan $ X $ rastgele değişkeninin varyansını hesaplayalım.

Örnek 7 ... $ X $ rastgele değişkeninin varyansının $ D \ left (X \ right) = 2 $'a eşit olduğu bilinmektedir. $ 4X + 1 $ rastgele değişkeninin varyansını bulun.

Yukarıdaki özellikleri kullanarak $ D \ left (4X + 1 \ right) = D \ left (4X \ right) + D \ left (1 \ right) = 4 ^ 2D \ sol (X \ sağ) + 0 = buluyoruz 16D \ sol (X \ sağ) = 16 \ cdot 2 = 32 $.

Örnek 8 ... $ X $ rastgele değişkeninin varyansının $ D \ left (X \ right) = 3 $'a eşit olduğu bilinmektedir. $ 3-2X $ rastgele değişkeninin varyansını bulun.

Yukarıdaki özellikleri kullanarak $ D \ left (3-2X \ right) = D \ left (3 \ right) + D \ left (2X \ sağ) = 0 + 2 ^ 2D \ left (X \ right) = buluyoruz 4D \ sol (X \ sağ) = 4 \ cdot 3 = 12 $.

4. Kesikli bir rastgele değişkenin dağılım fonksiyonu.

Kesikli bir rastgele değişkeni bir dağılım serisi şeklinde temsil etmenin yolu tek değildir ve en önemlisi, sürekli bir rastgele değişken bir dağılım serisi kullanılarak belirlenemediğinden evrensel değildir. Rastgele bir değişkeni temsil etmenin başka bir yolu daha vardır - dağıtım işlevi.

Dağıtım işlevi$ X $ rastgele değişkenine $ F \ left (x \ right) $ işlevi denir; bu, $ X $ rastgele değişkeninin sabit bir $ x $ değerinden daha küçük bir değer alma olasılığını belirler, yani, $ F \ sol (x \ sağ ) = P \ sol (X 6 $, sonra $ F \ sol (x \ sağ) = P \ sol (X = 1 \ sağ) + P \ sol (X = 2 \ sağ) + P \ sol (X = 3 \ sağ) + P \ sol (X = 4 \ sağ) + P \ sol (X = 5 \ sağ) + P \ sol (X = 6 \ sağ) = 1/6 + 1/ 6 + 1/6 + 1 / 6 + 1/6 + 1/6 = 1 $.

$ F \ left (x \ right) $ dağıtım fonksiyonunun grafiği:

Temel dağıtım yasaları

1.Binom dağılım yasası.

Binom dağılımı yasası, her denemede А olayının meydana gelme olasılığının p sabit olması koşuluyla, n bağımsız denemede А m kez olayının meydana gelme olasılığını tanımlar.

Örneğin, bir beyaz eşya mağazasındaki bir satış ekibi, 10 aramadan ortalama bir TV siparişi alır. m TV setinin satın alınması için olasılık dağılımı yasasını hazırlayın. Olasılık dağılım poligonunu oluşturun.

Tablo m - şirket tarafından bir TV satın almak için alınan siparişlerin sayısı. C n m, n için m TV setinin kombinasyon sayısıdır, p, A olayının meydana gelme olasılığıdır, yani. bir TV seti sipariş ederken, q, A olayının gerçekleşmeme olasılığıdır, yani. bir TV seti sipariş etmemek, P m, n, n'den m TV seti sipariş etme olasılığıdır. Şekil 1, olasılık dağılımının çokgenini göstermektedir.

2. Geometrik dağılım.

Rastgele değişkenin geometrik dağılımı aşağıdaki gibidir:

P m, m numaralı testte A olayının meydana gelme olasılığıdır.
p, bir denemede A olayının meydana gelme olasılığıdır.
q = 1 - p

Örnek. Bir ev aletleri onarım şirketi, çamaşır makineleri için 10 yedek bloktan oluşan bir parti aldı. Bir tarafın 1 kusurlu bloğu olduğu durumlar vardır. Arızalı bir blok bulunana kadar bir kontrol yapılır. Kontrol edilen blok sayısı için bir dağıtım yasası hazırlamak gerekir. Bir bloğun kusurlu olma olasılığı 0,1'dir. Olasılık dağılım poligonunu oluşturun.

Tablodan m sayısı arttıkça hatalı blok bulunma olasılığının azaldığı görülmektedir. Son satır (m = 10) iki olasılığı birleştirir: 1 - onuncu bloğun hatalı olduğu ortaya çıktı - 0.038742049, 2 - kontrol edilen tüm blokların çalıştığı ortaya çıktı - 0.34867844. Bir bloğun hatalı olma olasılığı nispeten düşük olduğundan (p = 0.1), son P m olayının (10 işaretli blok) olasılığı nispeten yüksektir. incir. 2.

3. Hipergeometrik dağılım.

Rastgele bir değişkenin hipergeometrik dağılımı aşağıdaki forma sahiptir:

Örneğin, 49'dan 7 tahmin edilen sayının dağıtım yasasını çizin. Bu örnekte, toplam sayılar N = 49, n = 7 sayı çıkarıldı, M - verilen özelliğe sahip tüm sayılar, yani doğru tahmin edilen sayılar, m - geri çekilenler arasında doğru tahmin edilen sayıların sayısı.

Tablo, bir m = 1 sayısını tahmin etme olasılığının, m = 0 durumundan daha yüksek olduğunu göstermektedir. Ancak, daha sonra olasılık hızla azalmaya başlar. Bu nedenle, 4 sayı tahmin etme olasılığı zaten 0,005'ten azdır ve 5 ihmal edilebilir.

4. Poisson dağıtım yasası.

Rastgele değişken X, dağıtım yasası şu şekildeyse bir Poisson dağılımına sahiptir:

Np = sabit
n, sonsuza giden deneme sayısıdır
p, sıfıra eğilimli bir olayın meydana gelme olasılığıdır.
m - A olayının oluşum sayısı

Örneğin, bir TV satış şirketi günde ortalama 100 arama almaktadır. Bir TV markası A sipariş etme olasılığı 0,08'dir; B - 0.06 ve C - 0.04. A, B ve C marka TV setlerinin satın alınması için siparişlerin dağıtım yasasını hazırlayın. Bir olasılık dağılım poligonu oluşturun.

Elde ettiğimiz koşuldan: m = 100,? 1 = 8,? 2 = 6,? 3 = 4 (? 10)

(tablonun tamamı verilmemiştir)

Eğer n yeterince büyükse ve sonsuza gidiyorsa ve p'nin değeri sıfıra gidiyorsa, böylece np çarpımı sabit bir sayıya yöneliyorsa, bu yasa iki terimli dağılım yasasına bir yaklaşımdır. Grafikten, p olasılığı ne kadar büyük olursa, eğrinin m eksenine o kadar yakın olduğu görülebilir, yani. daha düz. (Şek. 4)

Binom, geometrik, hipergeometrik ve Poisson dağılımlarının kesikli bir rastgele değişkenin olasılık dağılımını ifade ettiğine dikkat edilmelidir.

5. Tekdüze dağıtım yasası.

Olasılık yoğunluğu? (X) belirli bir aralıkta sabit bir değerse, dağılım yasasına tekdüze denir. Şekil 5, olasılık dağılım fonksiyonunun grafiklerini ve düzgün dağılım yasasının olasılık yoğunluğunu göstermektedir.

6. Normal dağılım yasası (Gauss yasası).

Sürekli rastgele değişkenlerin dağılım yasaları arasında en yaygın olanı normal dağılım yasasıdır. Bir rastgele değişken, olasılık yoğunluğu şu şekildeyse normal dağılım yasasına göre dağıtılır:

nerede
a, rastgele bir değişkenin matematiksel beklentisidir
? - standart sapma

Normal dağılım yasasına sahip bir rastgele değişkenin olasılık yoğunluğunun grafiği, x = a düz çizgisine göre simetriktir, yani x matematiksel beklentiye eşittir. Böylece, x = a ise, eğrinin maksimumu şuna eşittir:

Matematiksel beklentinin değeri değiştiğinde, eğri Ox ekseni boyunca kayar. Grafik (Şekil 6) x = 3'te eğrinin bir maksimuma sahip olduğunu gösterir, çünkü matematiksel beklenti 3'tür. Matematiksel beklenti farklı bir değer alırsa, örneğin a = 6, o zaman eğrinin maksimumu x = 6'dır. Standart sapmadan bahsetmişken, grafikten de görebileceğiniz gibi, standart sapma ne kadar büyük olursa, rastgele değişkenin olasılık yoğunluğunun maksimum değeri o kadar düşük olur.

Bir rasgele değişkenin (- ?, x) aralığındaki dağılımını ifade eden ve normal dağılım yasasına sahip olan fonksiyon, aşağıdaki formüle göre Laplace fonksiyonu cinsinden ifade edilir:

Şunlar. rastgele bir değişken X'in olasılığı iki bölümden oluşur: x'in eksi sonsuzdan a'ya, 0,5'e eşit ve ikinci kısım - a'dan x'e değerleri aldığı olasılıklar. (Şek. 7)

Birlikte öğrenmek

Öğrenciler için faydalı materyaller, diploma ve dönem ödevleri sipariş etmek

Ders: ayrık bir rastgele değişkenin dağılım yasası

Ayrık bir rastgele değişkenin dağılım yasası olası değerler ile olasılıkları arasındaki yazışmalara denir. Tablo, grafik ve analitik olarak ayarlanabilir.

Bu derste rasgele değişkenin ne olduğu tartışılmaktadır.

Tablo şeklinde ayarlamada, tablonun ilk satırı olası değerleri, ikincisi ise olasılıklarını içerir.

Bu değere dağıtım serisi denir. Ayrık rassal değişken.

X = x1, X = x2, X = xn tam bir grup oluşturur, çünkü bir testte rastgele bir değişken bir ve yalnızca bir olası değer alacaktır. Bu nedenle, olasılıklarının toplamı bire eşittir, yani p1 + p2 + pn = 1 veya

X'in değer kümesi sonsuz ise, o zaman Örnek 1. Nakit piyangoda 100 bilet verilir. 1000 rublelik bir kazanç ve 100 rublelik 10 kazanç çekilişe tabi tutulur. Rastgele değişken X'in dağıtım yasasını bulun - bir piyango biletinin sahibi için olası bir kazancın maliyeti.

Aranan dağıtım yasası aşağıdaki gibidir:

Kontrol; 0,01 + 0,1 + 0,89 = 1.
Dağılım yasasını ayarlamanın grafik yöntemiyle, noktalar (Xi: Pi) koordinat düzleminde çizilir ve ardından düz çizgi parçalarıyla birleştirilir. Ortaya çıkan kırık çizgi denir dağıtım poligonu.Örnek 1, dağılım poligonu Şekil 1'de gösterilmiştir.

Dağıtım yasasını belirlemenin analitik yönteminde, rastgele bir değişkenin olasılıklarını olası değerleriyle birleştiren bir formül belirtilir.

Ayrık dağılım örnekleri

Binom dağılımı

Her birinde A olayının sabit bir p olasılığı ile gerçekleştiği, bu nedenle sabit bir olasılıkla gerçekleşmediği n testi yapılmasına izin verin. Q = 1- P... Rastgele bir değişken düşünün X - bu n denemede A olayının oluşum sayısı. X'in olası değerleri x1 = 0, x2 = 1,…, xn + 1 = n'dir. Bunların olası olma olasılığı

Ayrık bir rastgele değişkenin dağılım yasasına Windows XP Word 2003 Excel 2003 denir. Ayrık rastgele değişkenlerin dağıtım yasaları Ayrık bir rastgele değişkenin dağılım yasası, bir rastgele değişkenin olası değerleri arasında bir ilişki kuran herhangi bir ilişkidir. değişken ve [...]

Rastgele değişken X'in dağılım yasası:

2. Örnek İlk atıcı için bir atıcı tarafından tek atışla hedefi vurma olasılığı 0.8, ikinci atıcı için - 0.85. Atıcılar hedefe bir el ateş etti. Olaylardan bağımsız olarak bireysel atıcılar için hedefi vurmayı göz önünde bulundurarak, A olayının olasılığını bulun - hedefe tam olarak bir isabet.
Çözüm.
A olayını düşünün - hedefe bir vuruş. Bu olayın meydana gelmesi için olası seçenekler aşağıdaki gibidir:

1. İlk atıcı vurur, ikinci atıcı ıskalar: P (A / H1) = p 1 * (1-p 2) = 0.8 * (1-0.85) = 0.12
2. İlk atıcı ıskaladı, ikinci atıcı hedefi vurdu: P (A / H2) = (1-p 1) * p 2 = (1-0.8) * 0.85 = 0.17
3. Birinci ve ikinci oklar birbirinden bağımsız olarak hedefi vurur: P (A / H1H2) = p 1 * p 2 = 0.8 * 0.85 = 0.68