üniforma dağıtımı Sürekli rasgele değişken, rasgele değişkenin değerlerinin her iki tarafta sınırlı olduğu ve aralığın sınırları içinde aynı olasılığa sahip olduğu bir dağılımdır. Bu, bu aralıkta olasılık yoğunluğunun sabit olduğu anlamına gelir.

Böylece, düzgün bir dağılımla, olasılık yoğunluğu şu forma sahiptir:

Değerler F(X) uç noktalarda A Ve B komplo ( A, B) belirtilmemiştir, çünkü sürekli bir rasgele değişken için bu noktalardan herhangi birine ulaşma olasılığı sıfırdır.

Düzgün dağılım eğrisi, çizime dayalı bir dikdörtgen biçimine sahiptir ( A, B) (Figurebelow), bu nedenle düzgün dağılıma bazen "dikdörtgen" dağılım denir.

Rastgele bir değişkene çarpma olasılığı nasıl bulunur? X, alana eşit olarak dağılmış ( A, B) herhangi bir parçaya ( α , β ) komplo ( A, B) ?

Bu olasılık formül ile bulunur.

ve aşağıdaki şekilde çift gölgeli alanı geometrik olarak temsil eder ve parçaya göre ( α , β ) komplo ( A, B) :

dağıtım işlevi F(X) düzgün bir dağılıma sahip sürekli bir rasgele değişkenin formuna sahiptir

Düzgün Dağılım Özellikleri

Düzgün dağılımın özellikleri:

Düzgün dağılım için örnekleri çözme

örnek 1 Gözlemler, sebzeleri taşımak için tasarlanan bir kutunun ağırlığının, 985 g ila 1025 g aralığında düzgün dağılmış bir rasgele değişken olduğunu göstermiştir.Bir kutu rasgele seçilir. Çözümde belirtilecek koşullar altında düzgün dağılmış bir rasgele değişkenin özelliklerini bulun.

Çözüm. Bu kutunun ağırlığının 995 ile 1005 arasında olma olasılığını bulalım:

Sürekli bir rastgele değişkenin ortalama değerini bulun:

.

Standart sapmayı bulalım:

.

Kutuların yüzde kaçının ortalama değerden bir standart sapma uzakta (yani, aralığında) bir ağırlığa sahip olduğunu belirleyelim:

.

Örnek 2 Metro trenleri 2 (dk.) aralıklarla düzenli olarak çalışır. Yolcu, tren tarifesiyle hiçbir ilgisi olmayan rastgele bir anda perona giriyor. rastgele değer T- treni beklemek zorunda kalacağı sürenin tek tip bir dağılımı vardır. Dağıtım yoğunluğunu bulun F(X) rastgele değişken T, matematiksel beklentisi, varyansı ve standart sapması. Yarım dakikadan fazla beklemeniz gerekme olasılığını bulun.

Çözüm. Dağıtım yoğunluğunu bulun F(X) :

F(X) = 1/2 (0 < X < 2) .

Rastgele bir değişkenin matematiksel beklentisini bulun:

μ = (2 + 0)/2 = 1 .

Varyansı bulalım:

σ ² = 2²/12 = 1/3.

Standart sapma:

σ = (√3)/3 .

Yolcunun treni en fazla yarım dakika beklemek zorunda kalma olasılığını bulun:

P{T < 1/2} = 1/4 .

Örnek 3 rastgele değer X alana eşit olarak dağıtılır ( A, B) . Deney sonucunda matematiksel beklentisinden 3'ten fazla sapma olasılığını bulun. σ .

Düzgün bir dağılım, rastgele bir değişkenin, aynı olasılıkla verilen sınırlar içindeki herhangi bir değeri alabildiği bir dağılımdır.

Rastgele bir değişkenin düzgün dağılımı, şekil 2'de gösterilmiştir. 5.9.

Pirinç. 5.9.

Düzgün dağılım olasılık yoğunluğu şu şekildedir:

burada a ve b, X rasgele değişkeninin varyasyon sınırlarını belirleyen yasanın parametreleridir.

Tekdüze dağılım yasası, özellikle alet desteklerindeki sürtünmeden kaynaklanan hatalara, hariç tutulmayan sistematik hata artıklarına, dijital aletlerdeki ayrıklaştırma hatalarına, seçici montaj sırasında aynı tasnif grubu içindeki boyutsal hatalara, parametrelerdeki hatalara tabidir. teknolojik toleransa göre daha dar sınırlar içinde seçilen ürünler, toplam işleme hatası

ayrılmaz

normalleştirilmiş Laplace işlevi olarak adlandırılır ve x - X farklı / \u003d - değerleri tablo halinde verilir. Hatası 10"5'ten küçük olan normalleştirilmiş Laplace işlevi Ф(/)'nin değeri aşağıdaki formülle belirlenebilir:

/>0 ise, Ф(/) = 7" ve eğer /< 0, то Ф(/) = 1-7". Функция Лапласа нечетная, т. е.

Negatif değerler için / tablo verileri eksi işareti ile alınır.

Normal dağılım yasasına uyan bir rastgele değişkenin ölçüldüğünde (x, x,) içinde bir değer alma olasılığı Ф (/) cinsinden aşağıdaki gibi yazılabilir:

Teorik bir normal dağılım eğrisinde, dalları asimptotik olarak apsis eksenine yaklaşır, yani x rasgele değişkeninin dağılım bölgesi ± oo içinde yer alır. Uygulamada, rastgele değişken x'in dağılım bölgesi sonlu limitlerle sınırlıdır.

Örneğin, rastgele bir değişkenin içinde olma olasılığı

baskın faktörün (kesici takımın aşınması, ısıl deformasyon vb.) zaman içindeki doğrusal değişimi, aletler üzerindeki ölçümlerden elde edilen değerlerin yuvarlanmasından kaynaklanan hatalar vb.

Düzgün dağılımın (kümülatif dağılım fonksiyonu) dağılım fonksiyonu F(x) aşağıdaki denklemle ifade edilir (a< х < Ь):

Dağılım fonksiyonunun şekli, Şek. 5.10.

Tekdüze bir dağılıma uyan rastgele bir değişkenin matematiksel beklentisi A / (x), varyansı 0 (x) ve standart sapması (a) şuna eşittir:

Uygulamada, düzgün bir dağılıma sahip sınırlayıcı başıboş alan co, b - a'ya eşittir veya (5.48), yani.

co = b - a = 2m/Ze.

Pirinç. 5.10.

Pirinç. 5.11.

Simpson Yasası

Üçgen dağılım eğrisinin görünümü şekil 2'de gösterilmektedir. 5.11. Olasılık yoğunluğu şu şekildedir:

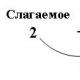
Bu yasaya göre, örneğin, düzgün dağılmış iki niceliğin toplamının (farkının) hataları dağıtılır. Örneğin, deliğin ve milin boyutlarındaki sapmalar tolerans alanları içinde eşit olarak dağılmışsa ve mil ile deliğin toleransları yaklaşık olarak aynıysa, boşluk toleransı içindeki boşluklar şuna göre dağıtılacaktır: üçgen kanunu Bu durumda boşluk olasılık yoğunluğu aşağıdaki forma sahip olacaktır:

nerede 5m(n, 5^ - sırasıyla, eklemdeki boşluğun minimum ve maksimum değerleri; .$m = ^"^^"la _ eklemdeki boşluğun ortalama değeri; /G5 = 5m1p - boşluk toleransı; l - boşluğun mevcut değeri.

Simpson yasasının dağıtım işlevi şu şekildedir:

İntegral dağılım fonksiyonunun grafiksel bir gösterimi, şekil 2'de gösterilmektedir. 5.12.

Simpson yasasına uyan rastgele bir değişkenin matematiksel beklentisi, varyansı ve standart sapması sırasıyla şuna eşittir:

Uygulamada, Simpson yasasına göre rastgele bir değişkenin dağılımı ile sınırlayıcı başıboş alan 2/'dir, yani

Olasılık yoğunluğunun tanımını hatırlayın.

Şimdi tekdüze olasılık dağılımı kavramını tanıtıyoruz:

Tanım 2

Rastgele bir değişkenin tüm olası değerlerini içeren bir aralıkta dağılım yoğunluğu sabitse, yani:

Resim 1.

Aşağıdaki dağıtım yoğunluğu özelliğini kullanarak $\ C$ sabitinin değerini bulun: $\int\limits^(+\infty )_(-\infty )(\varphi \left(x\right)dx)=1$

\[\int\limits^(+\infty )_(-\infty )(\varphi \left(x\right)dx)=\int\limits^a_(-\infty )(0dx)+\int\limits ^b_a(Cdx)+\int\limits^(+\infty )_b(0dx)=0+Cb-Ca+0=C(b-a)\] \ \

Böylece, tekdüze dağılım yoğunluk fonksiyonu şu şekildedir:

Şekil 2.

Grafik aşağıdaki forma sahiptir (Şekil 1):

Şekil 3. Düzgün olasılık dağılımının yoğunluğu

Düzgün Olasılık Dağılım Fonksiyonu

Şimdi düzgün bir dağılım için dağılım fonksiyonunu bulalım.

Bunu yapmak için şu formülü kullanacağız: $F\left(x\right)=\int\limits^x_(-\infty )(\varphi (x)dx)$

1. $x ≤ a$ için formüle göre şunu elde ederiz:

1. $a için

1. $x> 2$ için formüle göre şunu elde ederiz:

Böylece, dağıtım işlevi şu şekildedir:

Şekil 4

Grafik aşağıdaki forma sahiptir (Şekil 2):

Şekil 5. Düzgün olasılık dağılım fonksiyonu.

Rastgele bir değişkenin düzgün bir olasılık dağılımı altında $((\mathbf \alpha ),(\mathbf \beta ))$ aralığına düşme olasılığı

Rastgele bir değişkenin $(\alpha ,\beta)$ aralığına tek tip olasılık dağılımıyla düşme olasılığını bulmak için aşağıdaki formülü kullanacağız:

Beklenen değer:

Standart sapma:

Tekdüze bir olasılık dağılımı için problem çözme örnekleri

örnek 1

Troleybüsler arası 9 dakikadır.

Troleybüs yolcularını bekleyen $X$ rastgele değişkeninin dağılım fonksiyonunu ve dağılım yoğunluğunu derleyin.

Yolcunun troleybüsü üç dakikadan kısa sürede bekleme olasılığını bulunuz.

Yolcunun en az 4 dakikada troleybüs bekleme olasılığını bulunuz.

Matematiksel beklenti, varyans ve standart sapmayı bulun

1. Troleybüs beklemenin sürekli rasgele değişkeni $X$ düzgün dağıldığı için $a=0,\ b=9$.

Böylece, tekdüze olasılık dağılımının yoğunluk fonksiyonunun formülüne göre dağılım yoğunluğu şu şekildedir:

Şekil 6

Tek tip olasılık dağılım fonksiyonunun formülüne göre, bizim durumumuzda dağılım fonksiyonu şu şekildedir:

Şekil 7

1. Bu soru şu şekilde yeniden formüle edilebilir: düzgün dağılımlı rastgele bir değişkenin $\left(6,9\right)$ aralığına düşme olasılığını bulun.

Biz:

\}