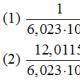DSV karakteristikleri ve özellikleri. Matematiksel beklenti, varyans, standart sapma

Dağılım yasası, rastgele değişkeni tamamen karakterize eder. Ancak, dağıtım yasasını bulmak imkansız olduğunda veya bu gerekli olmadığında, kendinizi sayısal özellikler adı verilen değerleri bulmakla sınırlayabilirsiniz. rastgele değişken... Bu değerler, rastgele bir değişkenin değerlerinin etrafında gruplandırıldığı bazı ortalama değerleri ve bunların bu ortalama değer etrafındaki dağılım derecesini belirler.

matematiksel beklenti ayrık bir rastgele değişken, hepsinin çarpımlarının toplamıdır. olası değerler olasılıklarına göre rastgele değişken.

Matematiksel beklenti, eşitliğin sağındaki seriler mutlak yakınsaksa vardır.

Olasılık açısından, matematiksel beklentinin, rastgele bir değişkenin gözlenen değerlerinin aritmetik ortalamasına yaklaşık olarak eşit olduğunu söyleyebiliriz.

Örnek. Kesikli bir rastgele değişkenin dağılım yasası bilinmektedir. Beklenen değeri bulun.

Çözüm:

9.2 Özellikler matematiksel beklenti

1. Sabit bir değerin matematiksel beklentisi en sabite eşittir.

2. Sabit faktör, matematiksel beklentinin işaretinin ötesinde çıkarılabilir.

3. İki bağımsız rastgele değişkenin çarpımının matematiksel beklentisi, onların matematiksel beklentilerinin çarpımına eşittir.

Bu özellik, rastgele sayıda rastgele değişken için geçerlidir.

4. İki rastgele değişkenin toplamının matematiksel beklentisi, terimlerin matematiksel beklentilerinin toplamına eşittir.

Bu özellik, rastgele sayıda rastgele değişken için de geçerlidir.

n bağımsız test yapılsın, A olayının gerçekleşme olasılığı p'ye eşit olsun.

Teorem. n bağımsız denemede A olayının meydana gelme sayısının matematiksel beklentisi M(X), deneme sayısının ve her denemede olayın meydana gelme olasılığının çarpımına eşittir.

Örnek. X ve Y'nin matematiksel beklentileri biliniyorsa, rastgele bir değişken Z'nin matematiksel beklentisini bulun: M (X) = 3, M (Y) = 2, Z = 2X + 3Y.

Çözüm:

9.3 Ayrık bir rastgele değişkenin dağılımı

Bununla birlikte, matematiksel beklenti, rastgele bir süreci tam olarak karakterize edemez. Matematiksel beklentiye ek olarak, rastgele değişkenin değerlerinin matematiksel beklentiden sapmasını karakterize eden bir değer girmek gerekir.

Bu sapma, rastgele değişken ile matematiksel beklentisi arasındaki farka eşittir. Bu durumda sapmanın matematiksel beklentisi sıfırdır. Bunun nedeni, bazı olası sapmaların olumlu, diğerlerinin olumsuz olması ve karşılıklı geri ödemelerinin bir sonucu olarak sıfır elde edilmesidir.

Dispersiyon (dispersiyon) kesikli bir rastgele değişken, rastgele değişkenin matematiksel beklentisinden sapmasının karesinin matematiksel beklentisi olarak adlandırılır.

Pratikte, varyansı hesaplamak için bu yöntem elverişsizdir, çünkü rastgele bir değişkenin çok sayıda değeri için hantal hesaplamalara yol açar.

Bu nedenle farklı bir yöntem kullanılmaktadır.

Teorem. Varyans, X rastgele değişkeninin karesinin matematiksel beklentisi ile matematiksel beklentisinin karesi arasındaki farka eşittir..

Kanıt. Matematiksel beklenti M (X) ve matematiksel beklenti M 2 (X)'in karesinin sabit değerler olduğu gerçeğini dikkate alarak şunu yazabiliriz:

Örnek. Dağılım kanunu tarafından verilen kesikli bir rastgele değişkenin varyansını bulun.

Çözüm: .

9.4 Dağılımın özellikleri

1. Sabitin varyansı sıfırdır. ...

2. Sabit faktörün karesi alınarak dağılım işaretinden çıkarılabilir. ...

3. İki bağımsız rastgele değişkenin toplamının varyansı, bu değerlerin varyanslarının toplamına eşittir. ...

4. İki bağımsız rastgele değişkenin farkının varyansı, bu değerlerin varyanslarının toplamına eşittir. ...

Teorem. Her birinde bir olayın meydana gelme olasılığının p sabit olduğu n bağımsız denemede bir A olayının meydana gelme sayısının varyansı, deneme sayısı ile gerçekleşme ve olmama olasılıklarının çarpımına eşittir. Her denemede bir olayın meydana gelmesi.

9.5 Ayrık bir rastgele değişkenin standart sapması

Ortalama kare sapma rastgele değişken X denir Kare kök varyanstan.

Teorem. Sonlu sayıda karşılıklı bağımsız rastgele değişkenin toplamının standart sapması, bu değerlerin standart sapmalarının karelerinin toplamının kareköküne eşittir.

- 10 yenidoğan arasındaki erkek çocuk sayısı.

Bu sayının önceden bilinmediği oldukça açıktır ve doğacak sonraki on çocukta şunlar olabilir:

Veya erkekler - bir ve sadece bir listelenen seçeneklerden.

Ve formda kalmak için biraz beden eğitimi:

- uzun atlama aralığı (bazı birimlerde).

Sporun ustası bile onu tahmin edemez :)

Ancak, hipoteziniz?

2) Sürekli rastgele değişken - alır herşey bazı sonlu veya sonsuz aralıktaki sayısal değerler.

Not : v eğitim literatürü popüler kısaltmalar DSV ve NSV

Önce, kesikli bir rastgele değişkeni analiz edelim, sonra - sürekli.

Ayrık bir rastgele değişkenin dağılım yasası

- bu yazışma bu miktarın olası değerleri ile olasılıkları arasında. Çoğu zaman, yasa bir tabloda yazılır:

Oldukça sık terim sıra dağıtım ama bazı durumlarda kulağa belirsiz geliyor ve bu yüzden "yasaya" bağlı kalacağım.

Ve şimdi çok önemli nokta : rastgele değişkenden beri mutlaka kabul edecek anlamlardan biri, ardından ilgili olaylar formu tam grup ve bunların oluşma olasılıklarının toplamı bire eşittir:

veya daraltılmış olarak yazılmışsa:

Örneğin, bir zara düşen noktaların olasılık dağılımı yasası aşağıdaki gibidir:

Yorum yok.

Ayrık bir rastgele değişkenin yalnızca "iyi" tamsayı değerleri alabileceği izlenimi altında olabilirsiniz. İllüzyonu ortadan kaldıralım - herhangi bir şey olabilirler:

örnek 1

Bazı oyunlarda aşağıdaki kazanan dağıtım yasası vardır:

... muhtemelen uzun zamandır bu tür görevlerin hayalini kurmuşsunuzdur :) Size bir sır vereceğim - ben de. Özellikle üzerinde çalışmayı bitirdikten sonra alan teorisi.

Çözüm: bir rastgele değişken üç değerden sadece birini alabildiğinden, karşılık gelen olaylar tam grup, bu, olasılıklarının toplamının bire eşit olduğu anlamına gelir:

"Partizan"ı ifşa edeceğiz:

- böylece, geleneksel birimleri kazanma olasılığı 0,4'tür.

Kontrol: ikna olmak için gerekli olan şey.

Cevap:

Dağıtım yasasının bağımsız olarak hazırlanmasının gerekli olduğu durumlar nadir değildir. Bunu yapmak için kullanın olasılığın klasik tanımı, olay olasılıkları için çarpma / toplama teoremleri ve diğer cipsler tervera:

Örnek 2

Kutu, 12'si kazanan, 2'si her biri 1.000 ruble ve geri kalanı - her biri 100 ruble olmak üzere 50 piyango bileti içerir. Rastgele bir değişkenin dağıtım yasasını çizin - kutudan rastgele bir bilet alınırsa ödemenin boyutu.

Çözüm: fark ettiğiniz gibi, rastgele bir değişkenin değerlerini düzenlemek gelenekseldir. artan düzen... Bu nedenle, en küçük kazançlarla, yani ruble ile başlıyoruz.

Toplamda 50 - 12 = 38 böyle bilet var ve klasik tanım:
- rastgele çekilen bir biletin kaybedilme olasılığı.

Davaların geri kalanı basit. Ruble kazanma olasılığı:

Kontrol edin: - ve bu, bu tür görevlerin özellikle hoş bir anı!

Cevap: ödemenin gerekli dağılımı:

Bağımsız çözüm için bir sonraki görev:

Örnek 3

Atıcının hedefi vurma olasılığı. Rastgele bir değişkenin dağılım yasasını çizin - 2 atıştan sonraki isabet sayısı.

...onu özlediğini biliyordum :) Hatırla çarpma ve toplama teoremleri... Çözüm ve cevap dersin sonunda.

Dağılım kanunu bir rastgele değişkeni tamamen tanımlar, ancak pratikte sadece bir kısmını bilmek faydalıdır (ve bazen daha faydalıdır). sayısal özellikler .

Ayrık bir rastgele değişkenin matematiksel beklentisi

Konuşuyorum basit dil, bu ortalama beklenen değer testlerin çoklu tekrarı ile. Rastgele bir değişkenin olasılıklı değerler almasına izin verin sırasıyla. O zaman belirli bir rastgele değişkenin matematiksel beklentisi ürünlerin toplamı tüm değerlerinden ilgili olasılıklara:

veya daraltılmış:

Örneğin, rastgele bir değişkenin matematiksel beklentisini - bir zarın üzerine düşen puan sayısını hesaplayalım:

Şimdi varsayımsal oyunumuzu hatırlayalım:

Soru ortaya çıkıyor: Bu oyunu oynamak hiç karlı mı? … Kimin nasıl bir izlenimi var? Yani sonuçta "hazır" ve söylemeyeceksin! Ancak bu soru, beklenen değeri hesaplayarak kolayca cevaplanabilir, aslında - ağırlıklı ortalama kazanma olasılıklarına göre:

Böylece, bu oyunun matematiksel beklentisi kaybetmek.

İzlenimlere güvenmeyin - sayılara güvenin!

Evet, burada arka arkaya 10 hatta 20-30 kez kazanabilirsiniz, ancak uzun vadede kaçınılmaz olarak mahvoluruz. Ve bu tür oyunları oynamanızı tavsiye etmem :) Eh, belki sadece eğlence için.

Yukarıdakilerin hepsinden, matematiksel beklentinin artık bir RANDOM değeri olmadığı sonucu çıkar.

Kendi kendine çalışma için yaratıcı ödev:

Örnek 4

Bay X, Avrupa ruletini aşağıdaki sisteme göre oynar: "kırmızı" üzerine sürekli olarak 100 ruble bahis yapar. Rastgele bir değişkenin dağıtım yasasını çizin - kazancı. Bir galibiyetin matematiksel beklentisini hesaplayın ve en yakın kopek'e yuvarlayın. kaç ortalama oyuncu her yüz bahiste kaybeder mi?

referans : Avrupa ruleti 18 kırmızı, 18 siyah ve 1 yeşil sektör ("sıfır") içerir. "Kırmızı" isabet durumunda, oyuncuya iki katı bahis ödenir, aksi takdirde kumarhanenin gelirine gider

Kendi olasılık tablolarınızı oluşturabileceğiniz daha birçok rulet sistemi vardır. Ancak bu, herhangi bir dağıtım kuralına ve tabloya ihtiyacımız olmadığında, oyuncunun matematiksel beklentisinin tam olarak aynı olacağı kesin olarak kurulduğu için böyledir. Sistemden sisteme sadece değişir

Ayrıca, cevaplarını görebileceğiniz bağımsız bir çözüm için görevler olacaktır.

Matematiksel beklenti ve varyans, bir rastgele değişkenin en sık kullanılan sayısal özellikleridir. Dağılımın en önemli özelliklerini karakterize ederler: konumu ve dağılım derecesi. Beklenen değer genellikle sadece ortalama olarak adlandırılır. rastgele değişken. Rastgele bir değişkenin dağılımı - dağılımın bir özelliği, rastgele bir değişkenin dağılımı matematiksel beklentisi hakkında.

Pek çok pratik problemde, bir rasgele değişkenin - dağıtım yasasının - eksiksiz, ayrıntılı bir özelliği ya elde edilemez ya da hiç gerekli değildir. Bu durumlarda, sayısal özellikler kullanılarak rastgele bir değişkenin yaklaşık açıklaması ile sınırlıdırlar.

Ayrık bir rastgele değişkenin matematiksel beklentisi

Gelelim matematiksel beklenti kavramına. Bir maddenin kütlesi apsis ekseninin noktaları arasında dağılsın x1 , x 2 , ..., x n... Ayrıca, her bir maddi noktanın, P1 , P 2 , ..., P n... Apsis ekseninde, kütlelerini dikkate alarak tüm malzeme noktaları sisteminin konumunu karakterize eden bir nokta seçmek gerekir. Maddi noktalar sisteminin kütle merkezini böyle bir nokta olarak almak doğaldır. Bu, rastgele bir değişkenin ağırlıklı ortalamasıdır. x, her noktanın apsisi xben karşılık gelen olasılığa eşit bir "ağırlık" ile girer. Bu şekilde elde edilen rastgele değişkenin ortalama değeri x matematiksel beklentisi denir.

Kesikli bir rasgele değişkenin matematiksel beklentisi, tüm olası değerlerinin çarpımlarının bu değerlerin olasılıklarıyla toplamıdır:

Örnek 1. Kazan-kazan piyangosu düzenlendi. Her biri 400'ü 10 ruble olan 1000 galibiyet var. Her biri 300 - 20 ruble 200 - 100 ruble. ve her biri 100 - 200 ruble. Bir bilet alıcısının ortalama kazancı nedir?

Çözüm. 10 * 400 + 20 * 300 + 100 * 200 + 200 * 100 = 50.000 ruble olan toplam kazanç miktarı 1000'e (toplam kazanç miktarı) bölünürse ortalama kazancı bulacağız. Sonra 50.000/1000 = 50 ruble alıyoruz. Ancak ortalama getiriyi hesaplama ifadesi aşağıdaki biçimde sunulabilir:

Öte yandan, bu koşullar altında kazanma miktarı 10, 20, 100 ve 200 ruble değerlerini alabilen rastgele bir değişkendir. sırasıyla 0,4'e eşit olasılıklarla; 0,3; 0.2; 0.1. Sonuç olarak, beklenen ortalama getiri, kazançların ürünlerinin toplamına ve bunların alınma olasılığına eşittir.

Örnek 2. Yayıncı yayınlamaya karar verdi. yeni kitap... Kitabı, 200, 50 - kitapçı ve 30 - yazar alacağı 280 rubleye satmayı planlıyor. Tablo, bir kitap yayınlamanın maliyeti ve kitabın belirli sayıda kopyasının satılma olasılığı hakkında bilgi sağlar.

Yayıncının beklenen kârını bulun.

Çözüm. Rastgele değer "kâr", satıştan elde edilen gelir ile gider maliyeti arasındaki farka eşittir. Örneğin, bir kitabın 500 kopyası satılırsa, satıştan elde edilen gelir 200 * 500 = 100.000 ve yayın maliyeti 225.000 ruble olur. Böylece, yayıncı 125.000 ruble zararla karşı karşıya. Aşağıdaki tablo, rastgele değişken - kârın beklenen değerlerini özetlemektedir:

Böylece, yayıncının kârının matematiksel beklentisini elde ederiz:

.

Örnek 3. Atış başına isabet olasılığı P= 0.2. 5'e eşit isabet sayısının matematiksel bir beklentisini sağlayan mermi tüketimini belirleyin.

Çözüm. Şimdiye kadar kullandığımız aynı matematiksel beklenti formülünden, x- mermi tüketimi:

.

Örnek 4. Rastgele bir değişkenin matematiksel beklentisini belirleyin x Her atış için isabet olasılığı varsa, üç atış için isabet sayısı P = 0,4 .

İpucu: rastgele bir değişkenin değerlerinin olasılığı şu şekilde bulunur: Bernoulli formülü .

Matematiksel beklenti özellikleri

Matematiksel beklentinin özelliklerini düşünün.

Mülkiyet 1. Bir sabitin matematiksel beklentisi şu sabite eşittir:

Mülkiyet 2. Sabit faktör, matematiksel beklentinin işaretinden çıkarılabilir:

Mülk 3. Rastgele değişkenlerin toplamının (farkının) matematiksel beklentisi, matematiksel beklentilerinin toplamına (farkına) eşittir:

Mülk 4. Rastgele değişkenlerin ürününün matematiksel beklentisi, matematiksel beklentilerinin ürününe eşittir:

Mülkiyet 5. Rastgele değişkenin tüm değerleri ise x aynı sayıda azalma (artma) İLE BİRLİKTE, o zaman matematiksel beklentisi aynı sayı kadar azalacaktır (artacaktır):

Yalnızca matematiksel beklentiyle sınırlandırılamadığınız zaman

Çoğu durumda, matematiksel beklenti tek başına rastgele bir değişkeni yeterince karakterize edemez.

Rastgele değişkenler olsun x ve Y aşağıdaki dağıtım yasaları tarafından verilmektedir:

Bu niceliklerin matematiksel beklentileri aynıdır - sıfıra eşittir:

Ancak, dağılımlarının doğası farklıdır. rastgele değer x sadece matematiksel beklentiden çok az farklı değerler alabilir ve rastgele değişken Y matematiksel beklentiden önemli ölçüde sapan değerler alabilir. Benzer bir örnek: Ortalama ücret, yüksek ve düşük ücretli işçilerin oranını yargılamayı imkansız kılıyor. Başka bir deyişle, matematiksel beklentiyle, ondan en azından ortalama olarak hangi sapmaların mümkün olduğunu yargılamak imkansızdır. Bunu yapmak için rastgele değişkenin varyansını bulmanız gerekir.

Ayrık bir rastgele değişkenin dağılımı

Dağılım Ayrık rassal değişken x matematiksel beklentiden sapmasının karesinin matematiksel beklentisine:

Rastgele bir değişkenin standart sapması x varyansının karekökünün aritmetik değeri denir:

.

Örnek 5. Rastgele değişkenlerin varyanslarını ve standart sapmalarını hesaplayın x ve Y, dağıtım yasaları yukarıdaki tablolarda verilmiştir.

Çözüm. Rastgele değişkenlerin matematiksel beklentileri x ve Y, yukarıda bulunan gibi, sıfıra eşittir. Dağılım formülüne göre E(NS)=E(y) = 0 elde ederiz:

Daha sonra rastgele değişkenlerin standart sapmaları x ve Y makyaj yapmak

.

Böylece aynı matematiksel beklentilerle rastgele değişkenin varyansı xçok küçük, ama rastgele bir değişken Y- önemli. Bu, dağılımlarındaki farklılığın bir sonucudur.

Örnek 6. Yatırımcının 4 adet alternatif yatırım projesi bulunmaktadır. Tablo, bu projelerde beklenen karı karşılık gelen olasılıkla özetlemektedir.

Her alternatif için matematiksel beklentiyi, varyansı ve standart sapmayı bulun.

Çözüm. 3. alternatif için bu değerlerin nasıl hesaplandığını gösterelim:

Tablo, tüm alternatifler için bulunan değerleri özetlemektedir.

Tüm alternatifler aynı matematiksel beklentilere sahiptir. Bu, uzun vadede herkesin aynı gelire sahip olduğu anlamına gelir. Standart sapma, risk için bir ölçü birimi olarak yorumlanabilir - ne kadar büyükse, yatırımın riski de o kadar büyük olur. Çok fazla risk istemeyen bir yatırımcı, en küçük standart sapmaya (0) sahip olduğu için proje 1'i seçecektir. Yatırımcı kısa sürede risk ve büyük getiri tercih ederse, o zaman en büyük standart sapmaya sahip projeyi seçecektir - proje 4.

Dağılım özellikleri

İşte varyansın özellikleri.

Mülkiyet 1. Sabitin varyansı sıfırdır:

Mülkiyet 2. Sabit faktör, karesini alarak varyans işaretinden çıkarılabilir:

.

Mülk 3. Rastgele bir değişkenin varyansı, niceliğin kendisinin matematiksel beklentisinin karesinin çıkarıldığı bu miktarın karesinin matematiksel beklentisine eşittir:

,

nerede .

Mülk 4. Rastgele değişkenlerin toplamının (farkının) varyansı, varyanslarının toplamına (farkına) eşittir:

Örnek 7. Ayrık bir rastgele değişken olduğu bilinmektedir. x sadece iki değer alır: -3 ve 7. Ayrıca matematiksel beklenti de bilinir: E(x) = 4. Ayrık bir rastgele değişkenin varyansını bulun.

Çözüm. ile belirtelim P rastgele bir değişkenin bir değer alma olasılığı x1 = −3 ... O halde değerin olasılığı x2 = 7 1 olacak - P... Matematiksel beklenti için denklemi türetelim:

E(x) = x 1 P + x 2 (1 − P) = −3P + 7(1 − P) = 4 ,

olasılıkları nereden alıyoruz: P= 0.3 ve 1 - P = 0,7 .

Rastgele bir değişkenin dağılım yasası:

Bu rastgele değişkenin varyansını, varyansın 3. özelliğinden formülle hesaplıyoruz:

NS(x) = 2,7 + 34,3 − 16 = 21 .

Rastgele bir değişkenin matematiksel beklentisini kendiniz bulun ve ardından çözüme bakın.

Örnek 8. Ayrık rassal değişken x sadece iki değer alır. 3 değerinden büyük olanı 0,4 olasılıkla kabul eder. Ayrıca rastgele değişkenin varyansı da bilinmektedir. NS(x) = 6. Rastgele bir değişkenin matematiksel beklentisini bulun.

Örnek 9. Kutuda 6 beyaz ve 4 siyah top vardır. Kutudan 3 top alınıyor. Çıkarılan toplar arasındaki beyaz topların sayısı kesikli bir rastgele değişkendir. x... Bu rastgele değişkenin matematiksel beklentisini ve varyansını bulun.

Çözüm. rastgele değer x 0, 1, 2, 3 değerlerini alabilir. olasılıkların çarpımı kuralı... Rastgele bir değişkenin dağılım yasası:

Dolayısıyla, belirli bir rastgele değişkenin matematiksel beklentisi:

m(x) = 3/10 + 1 + 1/2 = 1,8 .

Belirli bir rastgele değişkenin varyansı:

NS(x) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .

Sürekli bir rastgele değişkenin matematiksel beklentisi ve varyansı

Sürekli bir rastgele değişken için, matematiksel beklentinin mekanik yorumu aynı anlamı koruyacaktır: yoğunluk ile apsis ekseni üzerinde sürekli olarak dağıtılan bir birim kütle için kütle merkezi F(x). Fonksiyonun argümanının kullanıldığı ayrık bir rastgele değişkenin aksine xben aniden değişir, sürekli bir rastgele değişken için argüman sürekli değişir. Ancak sürekli bir rastgele değişkenin matematiksel beklentisi, ortalama değeriyle de ilişkilidir.

Sürekli bir rastgele değişkenin matematiksel beklentisini ve varyansını bulmak için belirli integralleri bulmanız gerekir. ... Sürekli bir rasgele değişkenin yoğunluk fonksiyonu verilirse, doğrudan integrale girer. Bir olasılık dağılım fonksiyonu verilirse, onu farklılaştırarak yoğunluk fonksiyonunu bulmanız gerekir.

Sürekli bir rastgele değişkenin tüm olası değerlerinin aritmetik ortalamasına denir. matematiksel beklenti, veya ile gösterilir.

Daha önce bilindiği gibi, dağıtım yasası rasgele değişkeni tamamen karakterize eder. Ancak, dağıtım yasası genellikle bilinmez ve kişi kendini daha az bilgiyle sınırlamak zorundadır. Bazen toplamda rastgele bir değişkeni tanımlayan sayıları kullanmak daha da kârlıdır; böyle numaralar denir rastgele bir değişkenin sayısal özellikleri.

Matematiksel beklenti önemli sayısal özelliklerden biridir.

Matematiksel beklenti, rastgele değişkenin ortalama değerine yaklaşık olarak eşittir.

Ayrık bir rastgele değişkenin matematiksel beklentisi tüm olası değerlerinin ürünlerinin toplamını olasılıklarına göre adlandırın.

Rastgele bir değişken sonlu bir dağılım serisi ile karakterize edilirse:

o zaman beklenen değer M (X) formülle belirlenir:

Sürekli bir rastgele değişkenin matematiksel beklentisi eşitlikle belirlenir:

rastgele değişkenin olasılık yoğunluğu nerede NS.

Örnek 4.7. Bir zar atarak düşen puan sayısının matematiksel beklentisini bulun.

Çözüm:

rastgele değer NS 1, 2, 3, 4, 5, 6 değerlerini alır. Dağılım yasasını oluşturalım:

O zaman matematiksel beklenti:

Matematiksel beklenti özellikleri:

1. Bir sabitin matematiksel beklentisi en sabite eşittir:

M (C) = C.

2. Sabit faktör, matematiksel beklentinin işaretinden çıkarılabilir:

M (CX) = CM (X).

3. İki bağımsız rastgele değişkenin çarpımının matematiksel beklentisi, matematiksel beklentilerinin çarpımına eşittir:

M (XY) = M (X) M (Y).

Örnek 4.8... Bağımsız rastgele değişkenler x ve Y aşağıdaki dağıtım yasaları tarafından verilmektedir:

XY rasgele değişkeninin matematiksel beklentisini bulun.

Çözüm.

Bu niceliklerin her birinin matematiksel beklentilerini bulalım:

Rastgele değişkenler x ve Y bağımsız, bu nedenle istenen matematiksel beklenti:

M (XY) = M (X) M (Y) =

Sonuç. Birbirinden bağımsız birkaç rastgele değişkenin çarpımının matematiksel beklentisi, onların matematiksel beklentilerinin çarpımına eşittir.

4. İki rastgele değişkenin toplamının matematiksel beklentisi, terimlerin matematiksel beklentilerinin toplamına eşittir:

M (X + Y) = M (X) + M (Y).

Sonuç. Birkaç rastgele değişkenin toplamının matematiksel beklentisi, terimlerin matematiksel beklentilerinin toplamına eşittir.

Örnek 4.9. Hedefe eşit isabet olasılığı ile 3 atış yapar s 1 = 0,4; p 2= 0.3 ve p 3= 0.6. Toplam isabet sayısının beklenen değerini bulun.

Çözüm.

İlk atıştaki isabet sayısı rastgele bir değişkendir 1 yalnızca iki değer alabilen: 1 (isabet) olasılıkla s 1= 0,4 ve 0 (kayıp) olasılıkla 1 = 1 – 0,4 = 0,6.

İlk atıştaki isabet sayısının matematiksel beklentisi, isabet olasılığına eşittir:

Benzer şekilde, ikinci ve üçüncü atışlardaki isabet sayısının matematiksel beklentilerini buluyoruz:

M (X 2)= 0.3 ve M(X 3) = 0,6.

Toplam isabet sayısı aynı zamanda üç atışın her birindeki isabetlerin toplamından oluşan rastgele bir değişkendir:

X = X1 + X2 + X3.

İstenilen matematiksel beklenti NS matematiksel olarak teoremle, toplamın beklentisini buluruz.

Olasılık teorisi, sadece üniversite öğrencileri tarafından incelenen özel bir matematik dalıdır. Hesaplamaları ve formülleri sever misiniz? Normal dağılım, topluluk entropisi, matematiksel beklenti ve ayrık bir rastgele değişkenin varyansı ile tanışma olasılığından korkmuyor musunuz? O zaman bu konu sizin için çok ilginç olacak. En önemlilerinden birkaçına göz atalım temel konseptler bu bilim bölümü.

Temel bilgileri hatırlayalım

Olasılık teorisinin en basit kavramlarını hatırlıyor olsanız bile makalenin ilk paragraflarını ihmal etmeyin. Gerçek şu ki, temelleri net bir şekilde anlamadan, aşağıda tartışılan formüllerle çalışamazsınız.

Yani, bazı rastgele olaylar olur, bazı deneyler. Gerçekleştirilen eylemlerin bir sonucu olarak, birkaç sonuç elde edebiliriz - bazıları daha yaygın, diğerleri daha az yaygındır. Bir olayın olasılığı, bir türden fiilen elde edilen sonuçların sayısının, toplam mümkün. Sadece bu kavramın klasik tanımını bilerek, sürekli rastgele değişkenlerin matematiksel beklentisini ve varyansını incelemeye başlayabilirsiniz.

Ortalama

Okula döndüğünüzde, matematik derslerinde aritmetik ortalama ile çalışmaya başladınız. Bu kavram, olasılık teorisinde yaygın olarak kullanılmaktadır ve bu nedenle göz ardı edilemez. Bizim için en önemli şey şu an rastgele bir değişkenin matematiksel beklentisi ve varyansı için formüllerde karşılaşacağımızdır.

Bir sayı dizimiz var ve aritmetik ortalamayı bulmak istiyoruz. Bizden istenen tek şey, mevcut her şeyi toplamak ve dizideki öğe sayısına bölmek. Diyelim ki 1'den 9'a kadar sayılar var. Elemanların toplamı 45 olacak ve bu değeri 9'a böleceğiz. Cevap: - 5.

Dağılım

Bilimsel anlamda varyans, bir özelliğin elde edilen değerlerinin aritmetik ortalamadan sapmalarının ortalama karesidir. Biri büyük Latince D harfi ile gösterilir. Bunu hesaplamak için neye ihtiyacınız var? Dizinin her elemanı için, mevcut sayı ile aritmetik ortalama arasındaki farkı hesaplayın ve karesini alın. Düşündüğümüz olay için tam olarak sonuçlar olabileceği kadar çok değer olacaktır. Ardından, alınan tüm öğeleri özetler ve dizideki öğelerin sayısına böleriz. Beş olası sonucumuz varsa, o zaman beşe böleriz.

Varyans, problem çözerken uygulanması için hatırlanması gereken özelliklere de sahiptir. Örneğin, rastgele bir değişken X kat artırıldığında, varyans X çarpı kare (yani, X * X) kadar artar. Asla sıfırdan küçük değildir ve değerlerin eşit bir değerde yukarı veya aşağı kaymasına bağlı değildir. Ayrıca bağımsız testler için toplamın varyansı, varyansların toplamına eşittir.

Şimdi ayrık bir rastgele değişkenin varyans örneklerini ve matematiksel beklentiyi kesinlikle dikkate almamız gerekiyor.

21 deney yaptığımızı ve 7 tane elde ettiğimizi varsayalım. farklı sonuçlar... Her birini sırasıyla 1,2,2,3,4,4 ve 5 kez gözlemledik. Varyans nedir?

İlk olarak, aritmetik ortalamayı hesaplayalım: öğelerin toplamı elbette 21'e eşittir. 7'ye bölün, 3 elde edin. Şimdi, orijinal dizideki her sayıdan 3 çıkarın, her bir değeri kareye alın ve ekleyin. birlikte sonuçlar. 12 ortaya çıkacak. Şimdi sayıyı eleman sayısına bölmemiz gerekiyor ve öyle görünüyor ki, hepsi bu. Ama bir yakalama var! Bunu tartışalım.

Deney sayısına bağımlılık

Varyans hesaplanırken paydanın iki sayıdan biri olabileceği ortaya çıktı: N veya N-1. Burada N, gerçekleştirilen deneylerin sayısı veya dizideki (esas olarak aynı olan) öğelerin sayısıdır. Bu neye bağlıdır?

Test sayısı yüzlerce ölçülürse, payda N'yi koymalıyız. Birimlerde ise, N-1. Bilim adamları sınırı oldukça sembolik olarak çizmeye karar verdiler: bugün 30 numarada çalışıyor. 30'dan az deney yaptıysak, toplamı N-1'e ve daha fazlaysa N'ye böleceğiz.

Görev

Varyans ve beklenti problemini çözme örneğimize geri dönelim. N veya N-1'e bölünmesi gereken bir ara sayı 12'ye sahibiz. 30'dan az olan 21 deney yaptığımız için ikinci seçeneği seçeceğiz. Yani cevap: varyans 12/2 = 2'dir.

Beklenen değer

Gelelim bu yazıda kesinlikle dikkate almamız gereken ikinci konsepte. Beklenen değer, karşılık gelen olasılıklarla çarpılan tüm olası sonuçların toplamıdır. Elde edilen değerin ve varyansın hesaplanmasının sonucunun, içinde kaç sonuç dikkate alınırsa alınsın, tüm problem için yalnızca bir kez elde edildiğini anlamak önemlidir.

Matematiksel beklentinin formülü oldukça basittir: sonucu alırız, olasılığıyla çarparız, aynısını ikinci, üçüncü sonuç için toplarız, vb. Bu kavramla ilgili her şeyi hesaplamak kolaydır. Örneğin, beklentilerin toplamı, toplamın beklentisine eşittir. Aynı şey bir iş için de geçerlidir. Olasılık teorisindeki her değer, bu kadar basit işlemlerin kendi başına yapılmasına izin vermez. Bir problem alalım ve incelediğimiz iki kavramın anlamlarını tek seferde hesaplayalım. Ek olarak, teori dikkatimizi dağıttı - uygulama zamanıydı.

Bir örnek daha

50 deneme yaptık ve farklı yüzdelerde meydana gelen 0'dan 9'a kadar 10 çeşit sonuç elde ettik. Bunlar sırasıyla: %2, %10, %4, %14, %2, %18, %6, %16, %10, %18'dir. Olasılıkları elde etmek için değerleri yüzde 100'e bölmeniz gerektiğini hatırlayın. Böylece 0,02 elde ederiz; 0.1, vb. Rastgele bir değişkenin varyansı ve matematiksel beklenti için problem çözme örneğini sunalım.

Aritmetik ortalamayı, hatırladığımız formülle hesaplıyoruz. ilkokul: 50/10 = 5.

Şimdi, saymayı kolaylaştırmak için olasılıkları "parçalar halinde" sonuç sayısına çevirelim. 1, 5, 2, 7, 1, 9, 3, 8, 5 ve 9 elde ederiz. Elde edilen her değerden aritmetik ortalamayı çıkarın, ardından elde edilen sonuçların her birinin karesini alırız. Örnek olarak ilk öğeyi kullanarak bunu nasıl yapacağınızı görün: 1 - 5 = (-). Sonraki: (-4) * (-4) = 16. Geri kalan değerler için bu işlemleri kendiniz yapın. Her şeyi doğru yaptıysanız, hepsini ekledikten sonra 90 alırsınız.

90'ı N'ye bölerek varyansı ve ortalamayı hesaplamaya devam edelim. Neden N-1 değil de N'yi seçiyoruz? Doğru, çünkü yapılan deney sayısı 30'u aşıyor. Yani: 90/10 = 9. Varyansı bulduk. Farklı bir numara alırsanız, umutsuzluğa kapılmayın. Büyük olasılıkla, hesaplamalarda yaygın bir hata yaptınız. Yazdıklarınızı tekrar kontrol edin ve kesinlikle her şey yerine oturacaktır.

Son olarak, matematiksel beklenti formülünü hatırlayalım. Tüm hesaplamaları vermeyeceğiz, sadece gerekli tüm prosedürleri tamamladıktan sonra kontrol edebileceğiniz cevabı yazacağız. Beklenti 5,48 olacak. Sadece ilk öğelerin örneğini kullanarak işlemlerin nasıl gerçekleştirileceğini hatırlayalım: 0 * 0.02 + 1 * 0.1 ... vb. Gördüğünüz gibi, sonucun değerini olasılık ile çarpıyoruz.

Sapma

Varyans ve matematiksel beklenti ile yakından ilgili bir diğer kavram da standart sapmadır. Latin harfleri sd veya Yunanca küçük harf "sigma" ile gösterilir. Bu kavram, değerlerin ortalama olarak merkezi özellikten ne kadar saptığını gösterir. Değerini bulmak için varyansın karekökünü hesaplamanız gerekir.

Normal dağılımı çizerseniz ve sapmanın karesini doğrudan üzerinde görmek istiyorsanız, bu birkaç adımda yapılabilir. Görüntünün yarısını modun soluna veya sağına alın (merkezi değer), ortaya çıkan şekillerin alanları eşit olacak şekilde yatay eksene dik çizin. Dağılımın ortası ile elde edilen yatay eksen üzerindeki izdüşüm arasındaki segmentin değeri standart sapmayı temsil edecektir.

Yazılım

Formüllerin açıklamalarından ve sunulan örneklerden de anlaşılacağı gibi, varyans ve matematiksel beklentinin hesaplanması aritmetik açıdan en basit prosedür değildir. Zaman kaybetmemek için yükseköğretimde kullanılan bir programı kullanmak mantıklıdır. Eğitim Kurumları- "R" denir. İstatistik ve olasılık teorisinden birçok kavram için değer hesaplamanıza olanak sağlayan fonksiyonlara sahiptir.

Örneğin, bir değer vektörü tanımlıyorsunuz. Bu şu şekilde yapılır: vektör<-c(1,5,2…). Теперь, когда вам потребуется посчитать какие-либо значения для этого вектора, вы пишете функцию и задаете его в качестве аргумента. Для нахождения дисперсии вам нужно будет использовать функцию var. Пример её использования: var(vector). Далее вы просто нажимаете «ввод» и получаете результат.

Nihayet

Dağılım ve matematiksel beklenti - bunlar olmadan gelecekte herhangi bir şeyi hesaplamak zordur. Üniversitelerdeki derslerin ana dersinde, konuyu incelemenin ilk aylarında zaten dikkate alınırlar. Tam da bu basit kavramların anlaşılmaması ve hesaplanamaması nedeniyle birçok öğrenci hemen programda geri kalmaya başlıyor ve daha sonra oturumda düşük notlar alıyor ve bu da onları burslardan mahrum bırakıyor.

Bu makalede sunulanlara benzer görevleri çözerek en az bir hafta, günde yarım saat pratik yapın. Ardından, olasılık teorisi üzerine yapılan herhangi bir testte, gereksiz ipuçları ve hile sayfaları olmadan örneklerle başa çıkacaksınız.