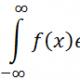vücut momentumu

Bir cismin momentumu, cismin kütlesi ile hızının çarpımına eşit bir niceliktir.

Maddi bir nokta olarak temsil edilebilecek bir bedenden bahsettiğimiz unutulmamalıdır. Bir cismin momentumuna ($p$) momentum da denir. Momentum kavramı fiziğe René Descartes (1596-1650) tarafından tanıtıldı. "Dürtü" terimi daha sonra ortaya çıktı (Latince'de dürtü "itme" anlamına gelir). Momentum bir vektör miktarıdır (hız gibi) ve aşağıdaki formülle ifade edilir:

$p↖(→)=mυ↖(→)$

Momentum vektörünün yönü her zaman hızın yönü ile çakışır.

SI'daki momentum birimi, $1$ m/s hızla hareket eden $1$ kg kütleli bir cismin momentumudur, dolayısıyla momentum birimi $1$ kg $·$ m/s'dir.

$∆t$ zaman aralığında bir cisme (madde noktasına) sabit bir kuvvet etki ederse, ivme de sabit olacaktır:

$a↖(→)=((υ_2)↖(→)-(υ_1)↖(→))/(∆t)$

$(υ_1)↖(→)$ ve $(υ_2)↖(→)$ cismin ilk ve son hızlarıdır. Bu değeri Newton'un ikinci yasasının ifadesinde yerine koyarsak şunu elde ederiz:

$(m((υ_2)↖(→)-(υ_1)↖(→)))/(∆t)=F↖(→)$

Köşeli parantezleri açarak ve cismin momentumu için ifadeyi kullanarak şunu elde ederiz:

$(p_2)↖(→)-(p_1)↖(→)=F↖(→)∆t$

Burada $(p_2)↖(→)-(p_1)↖(→)=∆p↖(→)$, $∆t$ zamana göre momentum değişimidir. O zaman önceki denklem şöyle olur:

$∆p↖(→)=F↖(→)∆t$

$∆p↖(→)=F↖(→)∆t$ ifadesi, Newton'un ikinci yasasının matematiksel bir temsilidir.

Bir kuvvetin çarpımı ve süresine denir kuvvet momentumu. Bu yüzden Bir noktanın momentumundaki değişim, ona etki eden kuvvetin momentumundaki değişime eşittir.

$∆p↖(→)=F↖(→)∆t$ ifadesi çağrılır vücut hareket denklemi. Aynı etkinin - bir noktanın momentumundaki değişiklik - küçük bir kuvvetle uzun bir sürede ve büyük bir kuvvetle kısa sürede elde edilebileceğine dikkat edilmelidir.

Sistemin impuls tel. momentum değişimi kanunu

Mekanik bir sistemin dürtüsü (momentumu), bu sistemin tüm malzeme noktalarının darbelerinin toplamına eşit bir vektördür:

$(p_(syst))↖(→)=(p_1)↖(→)+(p_2)↖(→)+...$

Değişim yasaları ve momentumun korunumu, Newton'un ikinci ve üçüncü yasalarının bir sonucudur.

İki gövdeden oluşan bir sistem düşünün. Sistemin gövdelerinin birbiriyle etkileştiği şekildeki kuvvetler ($F_(12)$ ve $F_(21)$) iç kuvvetler olarak adlandırılır.

Sisteme iç kuvvetlere ek olarak $(F_1)↖(→)$ ve $(F_2)↖(→)$ dış kuvvetleri etki etsin. Her cisim için $∆p↖(→)=F↖(→)∆t$ denklemi yazılabilir. Bu denklemlerin sol ve sağ kısımlarını toplayarak şunu elde ederiz:

$(∆p_1)↖(→)+(∆p_2)↖(→)=((F_(12))↖(→)+(F_(21))↖(→)+(F_1)↖(→)+ (F_2)↖(→))∆t$

Newton'un üçüncü yasasına göre $(F_(12))↖(→)=-(F_(21))↖(→)$.

Buradan,

$(∆p_1)↖(→)+(∆p_2)↖(→)=((F_1)↖(→)+(F_2)↖(→))∆t$

Sol tarafta, sistemin tüm cisimlerinin momentumundaki değişikliklerin geometrik toplamı, sistemin kendisinin momentumundaki değişime eşittir - $(∆p_(syst))↖(→)$. Bununla akılda tutularak $(∆p_1)↖(→)+(∆p_2) ↖(→)=((F_1)↖(→)+(F_2)↖(→))∆t$ eşitliği yazılabilir:

$(∆p_(sys))↖(→)=F↖(→)∆t$

$F↖(→)$, cisme etki eden tüm dış kuvvetlerin toplamıdır. Elde edilen sonuç, sadece dış kuvvetlerin sistemin momentumunu değiştirebileceği ve sistemin momentumundaki değişimin toplam dış kuvvetle aynı yönde olduğu anlamına gelir. Bu, mekanik bir sistemin momentumundaki değişim yasasının özüdür.

İç kuvvetler sistemin toplam momentumunu değiştiremez. Yalnızca sistemin bireysel organlarının dürtülerini değiştirirler.

Momentumun korunumu yasası

$(∆p_(syst))↖(→)=F↖(→)∆t$ denkleminden momentum korunum yasası çıkar. Sisteme hiçbir dış kuvvet etki etmiyorsa, $(∆p_(sys))↖(→)=F↖(→)∆t$ denkleminin sağ tarafı kaybolur, bu da sistemin toplam momentumunun değişmediği anlamına gelir :

$(∆p_(sys))↖(→)=m_1(υ_1)↖(→)+m_2(υ_2)↖(→)=sabit$

Hiçbir dış kuvvetin etki etmediği veya dış kuvvetlerin bileşkesinin sıfıra eşit olduğu sistemlere ne ad verilir? kapalı.

Momentumun korunumu yasası şunu belirtir:

Kapalı bir cisim sisteminin toplam momentumu, sistemin cisimlerinin birbirleriyle herhangi bir etkileşimi için sabit kalır.

Elde edilen sonuç, keyfi sayıda cisim içeren bir sistem için geçerlidir. Dış kuvvetlerin toplamı sıfıra eşit değilse, ancak bir yöndeki izdüşümlerinin toplamı sıfıra eşitse, sistemin momentumunun bu yöndeki izdüşümü değişmez. Bu nedenle, örneğin, tüm cisimlere etki eden yerçekimi kuvveti nedeniyle Dünya yüzeyindeki bir cisimler sistemi kapalı kabul edilemez, ancak, yatay yöndeki impuls izdüşümlerinin toplamı değişmeden kalabilir (yokluğunda) sürtünme), çünkü bu yönde yerçekimi kuvveti geçerli değildir.

jet tahrik

Momentumun korunumu yasasının geçerliliğini doğrulayan örnekleri ele alalım.

Bir çocuk lastik balonu alıp şişirelim ve bırakalım. Hava bir yönden dışarı çıkmaya başladığında balonun kendisinin diğer yöne doğru uçacağını göreceğiz. Topun hareketi, jet tahrikine bir örnektir. Momentumun korunumu yasası ile açıklanır: hava çıkışından önceki "top artı içindeki hava" sisteminin toplam momentumu sıfırdır; hareket sırasında sıfıra eşit kalmalıdır; bu nedenle top, jetin çıkış yönünün tersi yönde ve momentumu mutlak değer olarak hava jetinin momentumuna eşit olacak bir hızla hareket eder.

jet tahriki bir cismin bir parçasının ondan belli bir hızla ayrılmasıyla meydana gelen hareketine denir. Momentumun korunumu kanunu gereği, cismin hareket yönü, ayrılan parçanın hareket yönünün tersidir.

Roket uçuşları, jet tahrik prensibine dayanmaktadır. Modern bir uzay roketi çok karmaşık bir uçaktır. Roketin kütlesi, çalışma sıvısının kütlesinin (yani, yakıtın yanmasından kaynaklanan ve bir jet akışı şeklinde atılan sıcak gazlar) ve nihai veya dedikleri gibi "kuru" kütlenin toplamıdır. çalışma sıvısının roketten atılmasından sonra kalan roketin.

Bir roketten yüksek hızda bir reaktif gaz jeti fırlatıldığında, roketin kendisi ters yönde koşar. Momentum korunumu yasasına göre, roket tarafından elde edilen momentum $m_(p)υ_p$, fırlatılan gazların momentum $m_(gas) υ_(gas)$'a eşit olmalıdır:

$m_(p)υ_p=m_(gaz) υ_(gaz)$

Roketin hızını takip eder

$υ_p=((m_(gaz))/(m_p)) υ_(gaz)$

Bu formülden, roketin hızı ne kadar yüksek olursa, fırlatılan gazların hızı ve çalışma sıvısının kütlesinin (yani yakıt kütlesinin) nihai ("kuru") oranına oranı o kadar yüksek olabilir. roketin kütlesi.

$υ_p=((m_(gaz))/(m_p))·υ_(gaz)$ formülü yaklaşıktır. Yakıt yandıkça uçan roketin kütlesinin giderek küçüldüğünü hesaba katmaz. Bir roketin hızının kesin formülü 1897'de K. E. Tsiolkovsky tarafından elde edildi ve onun adını taşıyor.

Zorla çalışma

"İş" terimi fiziğe 1826'da Fransız bilim adamı J. Poncelet tarafından tanıtıldı. Günlük yaşamda yalnızca insan emeğine iş deniyorsa, o zaman fizikte ve özellikle mekanikte, işin zorla yapıldığı genel olarak kabul edilir. İşin fiziksel miktarı genellikle $A$ harfi ile gösterilir.

Zorla çalışma- bu, modülüne ve yönüne ve ayrıca kuvvetin uygulama noktasının yer değiştirmesine bağlı olarak bir kuvvetin hareketinin bir ölçüsüdür. Sabit bir kuvvet ve doğrusal hareket için iş şu eşitlikle belirlenir:

$A=F|∆r↖(→)|cosα$

$F$ cisme etki eden kuvvet, $∆r↖(→)$ yer değiştirme, $α$ kuvvet ile yer değiştirme arasındaki açıdır.

Kuvvetin işi, kuvvet ve yer değiştirme modüllerinin çarpımına ve bunlar arasındaki açının kosinüsüne, yani $F↖(→)$ ve $∆r↖(→)$ vektörlerinin skaler çarpımına eşittir.

İş, skaler bir niceliktir. $α 0$ ise ve $90° ise

Bir cisme birkaç kuvvet etki ettiğinde, toplam iş (tüm kuvvetlerin yaptığı işin toplamı), ortaya çıkan kuvvetin işine eşittir.

SI iş birimi joule($1$ J). $1$ J, $1$ N'lik bir kuvvetin bu kuvvet yönünde $1$ m'lik bir yolda yaptığı iştir. Bu birim, İngiliz bilim adamı J. Joule'nin (1818-1889) adını almıştır: $1$ J = $1$ N $·$ m Kilojul ve milijul de sıklıkla kullanılır: $1$ kJ $= 1,000$ J, $1$ mJ $ = 0.001$ J.

yerçekimi işi

Eğim açısı $α$ ve yüksekliği $H$ olan eğimli bir düzlem boyunca kayan bir cisim düşünelim.

$∆x$'ı $H$ ve $α$ cinsinden ifade ederiz:

$∆x=(H)/(sinα)$

$F_т=mg$ yerçekiminin hareket yönü ile bir açı ($90° - α$) yaptığı göz önüne alındığında, $∆x=(H)/(sin)α$ formülünü kullanarak yerçekimi işi için bir ifade elde ederiz. $A_g$:

$A_g=mg cos(90°-α)(H)/(sinα)=mgH$

Bu formülden, yerçekimi işinin yüksekliğe bağlı olduğu ve düzlemin eğim açısına bağlı olmadığı görülebilir.

Bundan şu sonuç çıkar:

1. yerçekimi işi, vücudun hareket ettiği yörüngenin şekline değil, yalnızca vücudun ilk ve son konumuna bağlıdır;
2. bir vücut kapalı bir yörünge boyunca hareket ettiğinde, yerçekimi işi sıfırdır, yani yerçekimi korunumlu bir kuvvettir (korunumlu kuvvetler bu özelliğe sahip kuvvetlerdir).

Tepki kuvvetlerinin çalışması, sıfırdır çünkü tepki kuvveti ($N$) $∆x$ yer değiştirmeye dik olarak yönlendirilir.

Sürtünme kuvvetinin yaptığı iş

Sürtünme kuvveti, $∆x$ deplasmanının karşısına yönlendirilir ve onunla $180°$ açı yapar, dolayısıyla sürtünme kuvvetinin işi negatiftir:

$A_(tr)=F_(tr)∆x cos180°=-F_(tr) ∆x$

$F_(tr)=μN, N=mg cosα, ∆x=l=(H)/(sinα),$ olduğundan

$A_(tr)=μmgHctgα$

Elastik kuvvetin işi

$F↖(→)$ bir dış kuvvetin $l_0$ uzunluğundaki gerilmemiş bir yayı $∆l_0=x_0$ kadar gererek etkimesine izin verin. $x=x_0F_(kontrol)=kx_0$ konumunda. $F↖(→)$ kuvvetinin $x_0$ noktasında sona ermesinden sonra, yay $F_(kontrol)$ kuvvetinin etkisi altında sıkıştırılır.

Yayın sağ ucunun koordinatı $х_0$'dan $х$'a değiştiğinde elastik kuvvetin işini belirleyelim. Bu alandaki elastik kuvvet doğrusal olarak değiştiğinden, Hooke yasasında bu alandaki ortalama değeri kullanılabilir:

$F_(ex.ort.)=(kx_0+kx)/(2)=(k)/(2)(x_0+x)$

O zaman iş ($(F_(exp.ort.))↖(→)$ ve $(∆x)↖(→)$ yönlerinin çakıştığı gerçeğini dikkate alarak) şuna eşittir:

$A_(exerc)=(k)/(2)(x_0+x)(x_0-x)=(kx_0^2)/(2)-(kx^2)/(2)$

Son formülün formunun $(F_(exp.ort.))↖(→)$ ve $(∆x)↖(→)$ arasındaki açıya bağlı olmadığı gösterilebilir. Elastik kuvvetlerin işi sadece yayın ilk ve son hallerindeki deformasyonlarına bağlıdır.

Bu nedenle, yerçekimi gibi elastik kuvvet korunumlu bir kuvvettir.

gücün gücü

Güç, işin üretildiği süreye oranıyla ölçülen fiziksel bir niceliktir.

Başka bir deyişle güç, birim zamanda ne kadar iş yapıldığını gösterir (SI cinsinden, $1$ s için).

Güç aşağıdaki formülle belirlenir:

$N$ güç, $A$ ise $∆t$ zamanında yapılan iştir.

$N=(A)/(∆t)$ formülünde $A$ çalışması yerine $A=F|(∆r)↖(→)|cosα$ ifadesi yerine şunu elde ederiz:

$N=(F|(∆r)↖(→)|cosα)/(∆t)=Fυcosα$

Güç, kuvvet ve hız vektörlerinin modüllerinin ürününe ve bu vektörler arasındaki açının kosinüsüne eşittir.

SI sistemindeki güç, watt (W) cinsinden ölçülür. Bir watt ($1$ W), $1$ J işin $1$ s'de yapıldığı güçtür: $1$ W $= 1$ J/s.

Bu birim, adını ilk buhar makinesini yapan İngiliz mucit J. Watt'tan (Watt) almıştır. J. Watt'ın kendisi (1736-1819), bir buhar makinesinin ve bir atın performansını karşılaştırabilmek için tanıttığı farklı bir güç - beygir gücü (hp) kullandı: 1 $ hp. $= 735.5$ Sal.

Teknolojide, genellikle daha büyük güç birimleri kullanılır - kilovat ve megavat: $1$ kW $= 1000$ W, $1$ MW $= 1000000$ W.

Kinetik enerji. Kinetik enerjinin değişim yasası

Bir cisim veya birkaç etkileşimli cisim (bir cisimler sistemi) iş yapabiliyorsa, o zaman enerjileri olduğunu söylerler.

"Enerji" kelimesi (Yunanca'dan. energia - eylem, aktivite) günlük yaşamda sıklıkla kullanılır. Yani, örneğin, hızlı bir şekilde iş yapabilen insanlara enerjik, büyük enerji ile denir.

Bir cismin hareket nedeniyle sahip olduğu enerjiye kinetik enerji denir.

Genel olarak enerjinin tanımında olduğu gibi kinetik enerji için de kinetik enerjinin hareket eden bir cismin iş yapabilme yeteneği olduğunu söyleyebiliriz.

$υ$ hızıyla hareket eden $m$ kütleli bir cismin kinetik enerjisini bulalım. Kinetik enerji hareketten kaynaklanan enerji olduğundan, onun için sıfır durumu, vücudun hareketsiz olduğu durumdur. Vücuda belirli bir hızı iletmek için gerekli işi bulduktan sonra, onun kinetik enerjisini bulacağız.

Bunu yapmak için, kuvvet vektörlerinin $F↖(→)$ ve yer değiştirme $∆r↖(→)$ yönleri çakıştığında $∆r↖(→)$ yer değiştirme kesiti üzerinde yapılan işi hesaplıyoruz. Bu durumda iş,

burada $∆x=∆r$

$α=const$ ivmeli bir noktanın hareketi için hareket ifadesi şu şekildedir:

$∆x=υ_1t+(at^2)/(2),$

$υ_1$ başlangıç ​​hızıdır.

$∆x=υ_1t+(at^2)/(2)$ ifadesinden $∆x$ ifadesini $A=F ∆x$ denkleminde değiştirerek ve Newton'un ikinci kanunu $F=ma$ kullanarak şunu elde ederiz:

$A=ma(υ_1t+(at^2)/(2))=(mat)/(2)(2υ_1+at)$

İvmeyi ilk $υ_1$ ve son $υ_2$ hızları cinsinden ifade etme $a=(υ_2-υ_1)/(t)$ ve yerine $A=ma(υ_1t+(at^2)/(2))=( mat)/ (2)(2υ_1+at)$ elimizde:

$A=(m(υ_2-υ_1))/(2) (2υ_1+υ_2-υ_1)$

$A=(mυ_2^2)/(2)-(mυ_1^2)/(2)$

Şimdi ilk hızı sıfıra eşitleyerek: $υ_1=0$, için bir ifade elde ederiz. kinetik enerji:

$E_K=(mυ)/(2)=(p^2)/(2m)$

Dolayısıyla hareket eden bir cismin kinetik enerjisi vardır. Bu enerji, cismin hızını sıfırdan $υ$'a çıkarmak için yapılması gereken işe eşittir.

$E_K=(mυ)/(2)=(p^2)/(2m)$'dan, bir cismi bir konumdan diğerine hareket ettirmek için yapılan kuvvetin kinetik enerjideki değişime eşit olduğu sonucu çıkar:

$A=E_(K_2)-E_(K_1)=∆E_K$

$A=E_(K_2)-E_(K_1)=∆E_K$ eşitliği ifade eder kinetik enerjideki değişim teoremi.

Vücudun kinetik enerjisindeki değişim(maddi nokta) belirli bir süre için cisme etki eden kuvvetin bu süre içinde yaptığı işe eşittir.

Potansiyel enerji

Potansiyel enerji, etkileşen cisimlerin veya aynı bedenin parçalarının karşılıklı düzenlenmesiyle belirlenen enerjidir.

Enerji, bir cismin iş yapma yeteneği olarak tanımlandığından, potansiyel enerji doğal olarak sadece cisimlerin göreli konumuna bağlı olan bir kuvvetin işi olarak tanımlanır. Bu, yerçekimi işi $A=mgh_1-mgh_2=mgH$ ve esneklik işidir:

$A=(kx_0^2)/(2)-(kx^2)/(2)$

Vücudun potansiyel enerjisi Dünya ile etkileşim, bu cismin kütlesi $m$ ile serbest düşüş ivmesi $g$ ve cismin Dünya yüzeyinden yüksekliğinin $h$ ürününe eşit değer olarak adlandırılır:

Elastik olarak deforme olmuş bir cismin potansiyel enerjisi, cismin esneklik katsayısı (sertlik) $k$ ile deformasyon karesinin $∆l$ çarpımının yarısına eşit değerdir:

$E_p=(1)/(2)k∆l^2$

$E_p=mgh$ ve $E_p=(1)/(2)k∆l^2$ hesaba katıldığında korunumlu kuvvetlerin (yerçekimi ve esneklik) işi şu şekilde ifade edilir:

$A=E_(p_1)-E_(p_2)=-(E_(p_2)-E_(p_1))=-∆E_p$

Bu formül, potansiyel enerjinin genel bir tanımını vermemizi sağlar.

Bir sistemin potansiyel enerjisi, sistemin başlangıç ​​durumundan son duruma geçişi sırasındaki değişimi sistemin iç muhafazakar kuvvetlerinin çalışmasına eşit olan cisimlerin konumuna bağlı bir değerdir; ters işaretle alınır.

$A=E_(p_1)-E_(p_2)=-(E_(p_2)-E_(p_1))=-∆E_p$ denkleminin sağ tarafındaki eksi işareti, işin iç kuvvetler tarafından yapıldığında ( örneğin "taş-toprak" sisteminde yerçekimi etkisi altında yere düşen cisim), sistemin enerjisi azalır. Bir sistemdeki iş ve potansiyel enerjideki değişim her zaman zıt işaretlere sahiptir.

İş, yalnızca potansiyel enerjideki değişimi belirlediğinden, mekanikte yalnızca enerjideki değişimin fiziksel anlamı vardır. Bu nedenle, sıfır enerji seviyesinin seçimi keyfidir ve yalnızca örneğin karşılık gelen denklemleri yazmanın kolaylığı gibi uygunluk hususlarıyla belirlenir.

Mekanik enerjinin değişim ve korunum yasası

Sistemin toplam mekanik enerjisi kinetik ve potansiyel enerjilerinin toplamına denir:

Cisimlerin konumu (potansiyel enerji) ve hızları (kinetik enerji) tarafından belirlenir.

Kinetik enerji teoremine göre,

$E_k-E_(k_1)=A_p+A_(pr),$

$А_р$ potansiyel kuvvetlerin işidir, $А_(p)$ potansiyel olmayan kuvvetlerin işidir.

Buna karşılık, potansiyel kuvvetlerin işi, cismin ilk $E_(p_1)$ ve son $E_p$ durumlarındaki potansiyel enerjisindeki farka eşittir. Bunu akılda tutarak, için bir ifade elde ederiz. mekanik enerjinin değişim yasası:

$(E_k+E_p)-(E_(k_1)+E_(p_1))=A_(pr)$

eşitliğin sol tarafı toplam mekanik enerjideki değişimi, sağ tarafı ise potansiyel olmayan kuvvetlerin işidir.

Bu yüzden, mekanik enerjinin değişim yasası okur:

Sistemin mekanik enerjisindeki değişim, tüm potansiyel olmayan kuvvetlerin işine eşittir.

Yalnızca potansiyel kuvvetlerin hareket ettiği mekanik bir sisteme muhafazakar denir.

Muhafazakar bir sistemde $A_(pr) = 0$. bu ima ediyor mekanik enerjinin korunumu yasası:

Kapalı muhafazakar bir sistemde, toplam mekanik enerji korunur (zamanla değişmez):

$E_k+E_p=E_(k_1)+E_(p_1)$

Mekanik enerjinin korunumu yasası, maddi noktalar (veya makro parçacıklar) sistemine uygulanabilen Newton mekaniği yasalarından türetilmiştir.

Bununla birlikte, mekanik enerjinin korunumu yasası, Newton yasalarının artık geçerli olmadığı bir mikro parçacık sistemi için de geçerlidir.

Mekanik enerjinin korunumu yasası, zamanın homojenliğinin bir sonucudur.

zamanın tekdüzeliği aynı başlangıç ​​koşulları altında fiziksel süreçlerin seyri, bu koşulların yaratıldığı ana bağlı değildir.

Toplam mekanik enerjinin korunumu yasası, korunumlu bir sistemdeki kinetik enerji değiştiğinde toplamlarının sabit kalması için potansiyel enerjisinin de değişmesi gerektiği anlamına gelir. Bu, bir tür enerjiyi diğerine dönüştürme olasılığı anlamına gelir.

Maddenin çeşitli hareket biçimlerine göre, çeşitli enerji türleri dikkate alınır: mekanik, iç (vücudun kütle merkezine göre moleküllerin kaotik hareketinin kinetik enerjisinin toplamına ve potansiyel enerjiye eşittir. moleküllerin birbirleriyle etkileşimi), elektromanyetik, kimyasal (elektronların hareketinin kinetik enerjisinden ve elektriğin birbirleriyle ve atom çekirdeği ile etkileşimlerinin enerjisinden oluşur), nükleer enerji vb. enerjinin farklı türlere bölünmesi oldukça keyfidir.

Doğal olaylara genellikle bir tür enerjinin diğerine dönüşümü eşlik eder. Bu nedenle, örneğin, çeşitli mekanizmaların parçalarının sürtünmesi, mekanik enerjinin ısıya, yani içsel enerji. Isı motorlarında ise tam tersine iç enerji mekanik enerjiye dönüştürülür; galvanik hücrelerde kimyasal enerji elektrik enerjisine vb. dönüştürülür.

Günümüzde enerji kavramı fiziğin temel kavramlarından biridir. Bu kavram, bir hareket biçiminin diğerine dönüşmesi fikriyle ayrılmaz bir şekilde bağlantılıdır.

Modern fizikte enerji kavramı şu şekilde formüle edilmiştir:

Enerji, her tür maddenin hareketinin ve etkileşiminin genel niceliksel bir ölçüsüdür. Enerji yoktan var olmaz ve yok olmaz, ancak bir biçimden diğerine geçebilir. Enerji kavramı, doğadaki tüm olguları birbirine bağlar.

basit mekanizmalar. mekanizma verimliliği

Basit mekanizmalar, vücuda uygulanan kuvvetlerin büyüklüğünü veya yönünü değiştiren cihazlardır.

Büyük yükleri çok az çabayla taşımak veya kaldırmak için kullanılırlar. Bunlar arasında kaldıraç ve çeşitleri - bloklar (hareketli ve sabit), bir kapı, eğimli bir düzlem ve çeşitleri - bir kama, bir vida vb.

Manivela. kaldıraç kuralı

Kol, sabit bir destek etrafında dönebilen sert bir gövdedir.

Kaldıraç kuralı diyor ki:

Bir kaldıraç, kendisine uygulanan kuvvetler kollarıyla ters orantılıysa dengededir:

$(F_2)/(F_1)=(l_1)/(l_2)$

$(F_2)/(F_1)=(l_1)/(l_2)$ formülünden, ona orantı özelliğini uygulayarak (oranın aşırı terimlerinin çarpımı, orta terimlerinin ürününe eşittir), biz aşağıdaki formülü elde edebilir:

Ancak $F_1l_1=M_1$, kolu saat yönünde döndürme eğiliminde olan kuvvet momentidir ve $F_2l_2=M_2$, kolu saat yönünün tersine döndürme eğiliminde olan kuvvet momentidir. Böylece, kanıtlanması gereken $M_1=M_2$.

Kaldıraç, eski çağlarda insanlar tarafından kullanılmaya başlandı. Yardımı ile eski Mısır'daki piramitlerin inşası sırasında ağır taş levhaları kaldırmak mümkün oldu. Kaldıraç olmadan, bu mümkün olmazdı. Nitekim örneğin 147$ m yüksekliğe sahip Cheops piramidinin inşası için en küçüğü 2.5$ ton olan iki milyondan fazla taş blok kullanıldı!

Günümüzde kaldıraçlar hem üretimde (örneğin vinçlerde) hem de günlük hayatta (makas, tel kesiciler, teraziler) yaygın olarak kullanılmaktadır.

sabit blok

Sabit bir bloğun hareketi, eşit kaldıraçlı bir kaldıracın hareketine benzer: $l_1=l_2=r$. Uygulanan kuvvet $F_1$, yüke $F_2$ eşittir ve denge koşulu:

sabit blok bir kuvvetin büyüklüğünü değiştirmeden yönünü değiştirmeniz gerektiğinde kullanılır.

hareketli blok

Hareket edebilen blok, kolları şu şekilde olan bir manivelaya benzer şekilde hareket eder: $l_2=(l_1)/(2)=r$. Bu durumda, denge koşulu şu şekildedir:

$F_1$ uygulanan kuvvet, $F_2$ ise yüktür. Hareketli bir bloğun kullanılması, iki kat güç artışı sağlar.

Polyspast (blok sistem)

Sıradan bir zincirli vinç, $n$ hareketli ve $n$ sabit bloktan oluşur. Bunu uygulamak, 2n$ kat güç artışı sağlar:

$F_1=(F_2)/(2n)$

Güç zincirli vinç n hareketli ve bir sabit bloktan oluşur. Bir güç zinciri vincinin kullanılması, 2^n$ kat güç artışı sağlar:

$F_1=(F_2)/(2^n)$

Vida

Vida, eksen üzerine sarılmış eğimli bir düzlemdir.

Vidaya etki eden kuvvetlerin dengesi için koşul şu şekildedir:

$F_1=(F_2h)/(2πr)=F_2tgα, F_1=(F_2h)/(2πR)$

burada $F_1$, vidaya uygulanan ve ekseninden $R$ uzaklıkta etki eden bir dış kuvvettir; $F_2$, vida ekseni yönünde etki eden kuvvettir; $h$ - vida adımı; $r$, ortalama diş yarıçapıdır; $α$ ipliğin açısıdır. $R$, vidayı $F_1$ kuvvetiyle döndüren kolun (anahtar) uzunluğudur.

Yeterlik

Performans katsayısı (COP) - yararlı işin harcanan tüm işe oranı.

Verimlilik genellikle yüzde olarak ifade edilir ve Yunanca $η$ ("bu") harfiyle gösterilir:

$η=(A_p)/(A_3) %100$

$A_n$ faydalı iş olduğunda, $A_3$ harcanan tüm iştir.

Yararlı çalışma, her zaman, bir kişinin şu veya bu mekanizmayı kullanarak harcadığı toplam çalışmanın yalnızca bir parçasıdır.

Yapılan işin bir kısmı sürtünme kuvvetlerinin üstesinden gelmek için harcanır. $А_3 > А_п$ olduğundan, verimlilik her zaman $1$'dan (veya $< 100%$).

Bu denklemdeki işlerin her biri, karşılık gelen kuvvetin ve kat edilen mesafenin ürünü olarak ifade edilebileceğinden, şu şekilde yeniden yazılabilir: $F_1s_1≈F_2s_2$.

Bundan şu sonuç çıkar ki, yürürlükteki mekanizmanın yardımıyla kazanırken, yolda aynı sayıda kaybederiz ve bunun tersi de geçerlidir.. Bu yasaya mekaniğin altın kuralı denir.

Mekaniğin altın kuralı, kullanılan cihazların parçalarının sürtünme ve yer çekiminin üstesinden gelme işini hesaba katmadığı için yaklaşık bir yasadır. Bununla birlikte, herhangi bir basit mekanizmanın işleyişini analiz ederken çok yararlı olabilir.

Bu nedenle, örneğin, bu kural sayesinde, şekilde gösterilen işçinin, kaldırma kuvvetinde 10 $ cm'lik çifte kazançla, kolun karşı ucunu 20 $ indirmesi gerekeceğini hemen söyleyebiliriz. santimetre.

Vücutların çarpışması. Elastik ve elastik olmayan etkiler

Momentumun ve mekanik enerjinin korunumu yasaları, bir çarpışmadan sonra cisimlerin hareketi problemini çözmek için kullanılır: Çarpışmadan önceki bilinen momentumlar ve enerjiler, bu miktarların çarpışmadan sonraki değerlerini belirlemek için kullanılır. Elastik ve elastik olmayan çarpma durumlarını göz önünde bulundurun.

Kesinlikle esnek olmayan bir etki denir, bundan sonra cisimler belirli bir hızda hareket eden tek bir cisim oluşturur. İkincisinin hızı sorunu, çarpmadan önce ve sonra kütleleri $m_1$ ve $m_2$ (iki cisimden bahsediyorsak) olan bir cisimler sistemi için momentumun korunumu yasası kullanılarak çözülür:

$m_1(υ_1)↖(→)+m_2(υ_2)↖(→)=(m_1+m_2)υ↖(→)$

Açıkçası, esnek olmayan bir çarpma sırasında cisimlerin kinetik enerjisi korunmaz (örneğin, $(υ_1)↖(→)=-(υ_2)↖(→)$ ve $m_1=m_2$'de sıfıra eşit olur. darbe).

Sadece impulsların toplamının değil, aynı zamanda çarpışan cisimlerin kinetik enerjilerinin toplamının da korunduğu mutlak elastik bir etki denir.

Mutlak elastik bir etki için, denklemler

$m_1(υ_1)↖(→)+m_2(υ_2)↖(→)=m_1(υ"_1)↖(→)+m_2(υ"_2)↖(→);$

$(m_(1)υ_1^2)/(2)+(m_(2)υ_2^2)/(2)=(m_1(υ"_1)^2)/(2)+(m_2(υ"_2) )^2)/(2)$

$m_1, m_2$ topların kütleleridir, $υ_1, υ_2$ topların çarpmadan önceki hızlarıdır, $υ"_1, υ"_2$ topların çarpmadan sonraki hızlarıdır.

3.2. Nabız

3.2.2. Vücut momentumundaki değişiklik

Momentumun değişim ve korunum yasalarını uygulamak için momentumdaki değişimi hesaplayabilmek gerekir.

Momentum değişikliğiΔ P → vücut formülle belirlenir

∆ P → = P → 2 - P → 1 ,

burada P → 1 = m v → 1 cismin ilk momentumudur; P → 2 = m v → 2 - son momentumu; m - vücut ağırlığı; v → 1 - vücudun ilk hızı; v → 2 son hızıdır.

Vücut momentumundaki değişikliği hesaplamak için aşağıdaki algoritmanın kullanılması tavsiye edilir:

1) bir koordinat sistemi seçin ve cismin ilk P → 1 ve son P → 2 momentumlarının koordinat eksenlerine izdüşümlerini bulun:

P1x, P2x;

P 1 y , P 2 y ;

∆P x = P 2 x - P 1 x ;

∆P y = P 2 y - P 1 y ;

3) momentum değişim vektörü Δ P →'nin modülünü şu şekilde hesaplayın:

ΔP = ΔPx2 + ΔPy2 .

Örnek 4. Bir cisim dikeyle 30° açı yapacak şekilde yatay bir düzleme düşüyor. Uçakla temas anında cismin momentum modülü 15 kg m/s ise, çarpma sırasında cismin momentumundaki değişim modülünü belirleyin. Bir cismin bir düzlem üzerindeki etkisinin kesinlikle elastik olduğu varsayılır.

Çözüm. Yatay bir yüzey üzerine düşeye α açısı yaparak düşen ve bu yüzeyle çarpışan bir cisim mutlak elastiktir,

• ilk olarak, hızının modülünü ve dolayısıyla momentumun büyüklüğünü değişmeden tutar:

P 1 \u003d P 2 \u003d P;

• ikincisi, yüzeyden üzerine düştüğü açıyla yansıtılır:

α 1 = α 2 = α,

nerede P 1 \u003d mv 1 - çarpmadan önceki vücudun momentum modülü; P 2 \u003d mv 2 - çarpmadan sonra vücudun momentum modülü; m - vücut ağırlığı; v 1 - vücudun çarpmadan önceki hızının değeri; v 2 - çarpmadan sonra vücudun hızının değeri; α 1 - geliş açısı; α 2 - yansıma açısı.

Belirtilen vücut impulsları, açıları ve koordinat sistemi şekilde gösterilmiştir.

Vücudun momentumundaki değişim modülünü hesaplamak için aşağıdaki algoritmayı kullanırız:

1) Vücudun yüzeye çarpmasından önceki ve sonraki impulsların izdüşümlerini koordinat eksenlerine yazarız:

P 1 x = mv  sin α, P 2 x = mv  sin α;

P 1 y = −mv  cos α, P 2 y = mv  cos α;

2) formülleri kullanarak momentum değişiminin koordinat eksenlerindeki izdüşümlerini bulun

Δ P x \u003d P 2 x - P 1 x \u003d m v sin α - m v sin α \u003d 0;

Δ P y = P 2 y - P 1 y = m v çünkü α - (− m v çünkü α) = 2 m v çünkü α ;

Δ P = (Δ P x) 2 + (Δ P y) 2 = (Δ P y) 2 = | ∆P y | = 2 m v cos α .

P = mv değeri problemin koşulunda belirtilir; bu nedenle, momentumdaki değişim modülünü formülle hesaplayacağız.

Δ P = 2 P cos 30 ° = 2 ⋅ 15 ⋅ 0,5 3 ≈ 26 kg ⋅ m/s.

Örnek 5. Kütlesi 50 g olan bir taş ufka 45° açı yapacak şekilde 20 m/s hızla fırlatılıyor. Uçuş sırasında taşın momentumundaki değişim modülünü bulun. Hava direncini ihmal edin.

Çözüm. Hava direnci yoksa, vücut simetrik bir parabol boyunca hareket eder; burada

• ilk olarak, cismin çarpma noktasındaki hız vektörü ufukla α açısına eşit bir β açısı yapar (α, cismin çarpma noktasındaki hız vektörü ile ufuk arasındaki açıdır):

• ikincisi, v 0 fırlatma noktasındaki ve v gövdesinin düşme noktasındaki hız modülleri de aynıdır:

v 0 = v ,

nerede v 0 - vücudun atış noktasındaki hızının değeri; v, vücudun düşme noktasındaki hızıdır; α, cismi fırlatma noktasında hız vektörünün ufukla yaptığı açıdır; β, vücudun düşme noktasında hız vektörünün ufukla yaptığı açıdır.

Vücut hız vektörleri (momentum vektörleri) ve açılar şekilde gösterilmiştir.

Uçuş sırasında vücudun momentumundaki değişim modülünü hesaplamak için aşağıdaki algoritmayı kullanırız:

1) fırlatma noktası ve düşme noktası için impulsların projeksiyonlarını koordinat eksenlerine yazın:

P 1 x = mv 0  cos α, P 2 x = mv 0  cos α;

P 1 y = mv 0  sin α, P 2 y = −mv 0  sin α;

2) formülleri kullanarak momentum değişiminin koordinat eksenlerindeki izdüşümlerini bulun

Δ P x \u003d P 2 x - P 1 x \u003d m v 0 çünkü α - m v 0 çünkü α \u003d 0;

Δ P y \u003d P 2 y - P 1 y \u003d - m v 0 sin α - m v 0 sin α \u003d - 2 m v 0 sin α;

3) momentum modülünü şu şekilde hesaplayın:

Δ P = (Δ P x) 2 + (Δ P y) 2 = (Δ P y) 2 = | ∆P y | \u003d 2 m v 0 sin α,

nerede m - vücut ağırlığı; v 0 - vücudun ilk hızının modülü.

Bu nedenle, momentumdaki değişim modülünü formülle hesaplayacağız.

Δ P = 2 m v 0 sin 45 ° = 2 ⋅ 50 ⋅ 10 − 3 ⋅ 20 ⋅ 0,5 2 ≈ 1,4 kg ⋅ m/s.

Newton yasaları, cisimlerin etkileşimi ve hareketi ile ilgili pratik olarak önemli çeşitli sorunları çözmeyi mümkün kılar. Örneğin, bu cisme etki eden tüm kuvvetler biliniyorsa, hareket eden bir cismin ivmesini bulmak gibi çok sayıda bu tür problem bağlantılıdır. Ve sonra diğer miktarlar ivme ile belirlenir (anlık hız, yer değiştirme vb.).

Ancak vücuda etki eden kuvvetleri belirlemek genellikle çok zordur. Bu nedenle, birçok sorunu çözmek için başka bir önemli fiziksel nicelik kullanılır - vücudun momentumu.

• Bir cismin momentumu p, cismin kütlesi ile hızının çarpımına eşit bir vektör fiziksel niceliktir.

Momentum bir vektör miktarıdır. Cismin momentum vektörünün yönü her zaman hız vektörünün yönü ile çakışır.

SI'daki momentum birimi, 1 m/s hızla hareket eden 1 kg kütleli bir cismin momentumudur. Bu, SI cinsinden bir cismin momentum biriminin 1 kg m/s olduğu anlamına gelir.

Hesaplarken, vektörlerin projeksiyonları için denklemi kullanırlar: p x \u003d mv x.

Seçilen X eksenine göre hız vektörünün yönüne bağlı olarak, momentum vektörünün izdüşümü pozitif veya negatif olabilir.

Latince "impulse" (impulsus) kelimesi "itme" anlamına gelir. Bazı kitaplar momentum yerine momentum terimini kullanır.

Bu nicelik, Newton'un daha sonra onun adını alacak yasaları keşfettiği sıralarda (yani 17. yüzyılın sonunda) bilime girdi.

Vücutlar etkileşime girdiğinde, momentumları değişebilir. Bu basit bir deneyle doğrulanabilir.

Aynı kütleye sahip iki top, Şekil 44 a'da gösterildiği gibi, bir tripod halkasına sabitlenmiş ahşap bir cetvele iplik halkalarına asılmıştır.

Pirinç. 44. Momentumun Korunumu Yasasının Gösterimi

Top 2 dikeyden a açısı kadar saptırılır (Şek. 44, b) ve serbest bırakılır. Önceki konumuna dönerek topa 1 vurur ve durur. Bu durumda top 1 harekete geçer ve aynı a açısı kadar sapar (Şekil 44, c).

Bu durumda, topların etkileşiminin bir sonucu olarak, her birinin momentumunun değiştiği açıktır: top 2'nin momentumu ne kadar azaldıysa, top 1'in momentumu aynı miktarda arttı.

İki veya daha fazla cisim sadece birbirleriyle etkileşime giriyorsa (yani dış kuvvetlere maruz kalmıyorlarsa), bu cisimler kapalı bir sistem oluşturur.

Kapalı bir sisteme dahil olan cisimlerin her birinin momentumu, birbirleriyle etkileşimleri sonucunda değişebilir. Ancak

• kapalı bir sistemi oluşturan cisimlerin impulslarının vektörel toplamı, bu cisimlerin herhangi bir hareketi ve etkileşimi için zamanla değişmez.

Bu, momentumun korunumu yasasıdır.

Momentumun korunumu yasası, vektör toplamı sıfıra eşit olan sistemin gövdelerine dış kuvvetler etki ederse de yerine getirilir. Bunu, momentumun korunumu yasasını türetmek için Newton'un ikinci ve üçüncü yasalarını kullanarak gösterelim. Basit olması için, yalnızca iki gövdeden oluşan bir sistemi düşünün - kütleleri m 1 ve m 2 olan ve v 1 ve v 2 hızlarıyla birbirlerine doğru doğrusal olarak hareket eden toplar (Şekil 45).

Pirinç. 45. İki cisimden oluşan bir sistem - birbirine doğru düz bir çizgide hareket eden toplar

Topların her birine etki eden yerçekimi kuvvetleri, üzerinde yuvarlandıkları yüzeyin elastik kuvvetleri ile dengelenir. Dolayısıyla, bu kuvvetlerin etkisi göz ardı edilebilir. Bu durumda harekete karşı direnç güçleri küçüktür, bu nedenle etkilerini de dikkate almayacağız. Böylece topların sadece birbirleriyle etkileştiğini varsayabiliriz.

Şekil 45, bir süre sonra topların çarpışacağını göstermektedir. Çok kısa bir süre t süren bir çarpışma sırasında, sırasıyla birinci ve ikinci toplara uygulanan F 1 ve F 2 etkileşim kuvvetleri ortaya çıkacaktır. Kuvvetlerin hareketi sonucunda topların hızları değişecektir. Topların çarpışmadan sonraki hızlarını v 1 ve v 2 harfleriyle gösterelim.

Newton'un üçüncü yasasına göre, topların etkileşim kuvvetleri mutlak değerde eşittir ve zıt yönlerdedir:

Newton'un ikinci yasasına göre, bu kuvvetlerin her biri, etkileşim sırasında topların her biri tarafından alınan kütle ve ivmenin ürünü ile değiştirilebilir:

m 1 bir 1 \u003d -m 2 bir 2.

Bildiğiniz gibi ivmeler eşitliklerden belirlenir:

İvme kuvvetleri için denklemdeki karşılık gelen ifadeleri değiştirerek şunu elde ederiz:

Eşitliğin her iki tarafını da t ile azaltmanın bir sonucu olarak şunu elde ederiz:

m1 (v "1 - v 1) \u003d -m 2 (v" 2 - v 2).

Bu denklemin terimlerini aşağıdaki gibi gruplandırırız:

m 1 v 1 "+ m 2 v 2" = m 1 v 1 = m 2 v 2. (1)

mv = p olduğunu göz önünde bulundurarak, denklemi (1) aşağıdaki biçimde yazarız:

P "1 + P" 2 \u003d P 1 + P 2. (2)

Denklem (1) ve (2)'nin sol kısımları topların etkileşimlerinden sonraki toplam momentumunu, sağ kısımları ise etkileşimden önceki toplam momentumunu göstermektedir.

Bu, etkileşim sırasında topların her birinin momentumunun değişmesine rağmen, etkileşimden sonraki momentumlarının vektör toplamının etkileşimden öncekiyle aynı kaldığı anlamına gelir.

Denklemler (1) ve (2), momentumun korunumu yasasının matematiksel kaydıdır.

Bu kurs yalnızca tek bir düz çizgi boyunca hareket eden cisimlerin etkileşimlerini ele aldığından, momentumun korunumu yasasını skaler formda yazmak için, vektör niceliklerinin X ekseni üzerindeki izdüşümlerini içeren bir denklem yeterlidir:

m 1 v "1x + m 2 v" 2x \u003d m 1 v 1x + m 2 v 2x.

Sorular

1. Vücudun momentumuna ne denir?
2. Momentum vektörlerinin yönleri ve hareket eden bir cismin hızı hakkında ne söylenebilir?
3. Bize Şekil 44'te gösterilen deneyin gidişatından bahsedin. Bu neyi gösteriyor?
4. Birkaç cismin kapalı bir sistem oluşturduğu ifadesi ne anlama geliyor?
5. Momentumun korunumu yasasını formüle edin.
6. İki cisimden oluşan kapalı bir sistem için, momentumun korunumu yasasını bu cisimlerin kütlelerini ve hızlarını içeren bir denklem şeklinde yazın. Bu denklemdeki her sembolün ne anlama geldiğini açıklayın.

Alıştırma 20

1. Her biri 0,2 kg ağırlığındaki iki oyuncak saat makinesi düz bir çizgide birbirine doğru hareket eder. Her makinenin yere göre hızı 0,1 m/s'dir. Makinelerin momentum vektörleri eşit mi; momentum vektörlerinin modülleri? Yörüngelerine paralel olarak, makinelerin her birinin momentumunun X ekseni üzerindeki izdüşümünü belirleyin.
2. Kütlesi 1 ton olan bir arabanın hızı 54'ten 72 km/s'ye değiştiğinde momentumu (mutlak değer olarak) ne kadar değişir?
3. Bir adam gölün yüzeyinde dinlenen bir teknede oturuyor. Bir noktada ayağa kalkar ve kıçtan pruvaya gider. Tekne ne olacak? Olayı momentumun korunumu yasasına göre açıklayınız.
4. 35 ton ağırlığındaki bir vagon, aynı hat üzerinde duran 28 ton ağırlığındaki bir vagona yanaşıyor ve otomatik olarak onunla eşleşiyor. Bağlandıktan sonra arabalar düz bir çizgide 0,5 m/s hızla hareket ederler. 35 ton ağırlığındaki arabanın bağlanmadan önceki hızı ne kadardı?

Genellikle fizikte bir cismin momentumundan söz edilir, bu da hareket miktarını ima eder. Aslında, bu kavram tamamen farklı bir nicelikle - kuvvetle - yakından bağlantılıdır. Kuvvet dürtüsü - nedir, fiziğe nasıl dahil edilir ve anlamı nedir: tüm bu konular makalede ayrıntılı olarak ele alınmıştır.

hareket sayısı

Vücudun dürtüsü ve kuvvetin dürtüsü birbiriyle ilişkili iki niceliktir, ayrıca pratikte aynı anlama gelirler. Öncelikle momentum kavramına bir göz atalım.

Fiziksel bir nicelik olarak hareket miktarı, ilk olarak modern bilim adamlarının bilimsel çalışmalarında, özellikle 17. yüzyılda ortaya çıktı. Burada iki rakama dikkat etmek önemlidir: Tartışılan niceliği impeto (dürtü) olarak adlandıran ünlü İtalyan Galileo Galilei ve motus'un (hareket) büyüklüğüne ek olarak aynı zamanda büyük İngiliz Isaac Newton da kullandı. vis motrix (itici güç) kavramı.

Böylece, yukarıda adı geçen bilim adamları, bir nesnenin kütlesinin ürünü ile uzaydaki doğrusal hareketinin hızını hareket miktarı olarak anladılar. Bu tanım matematik dilinde şöyle yazılmıştır:

Hız modülüyle orantılı olan vücut hareketi yönüne yönelik vektör değerinden (p¯) bahsettiğimize ve vücut kütlesinin orantılılık katsayısının rolünü oynadığına dikkat edin.

Kuvvetin momentumu ile p¯'deki değişim arasındaki ilişki

Yukarıda bahsedildiği gibi, momentuma ek olarak Newton, itici güç kavramını da tanıttı. Bunu şöyle tanımladı:

Bu, üzerine etki eden bazı dış kuvvetler F¯ sonucunda bir cisim üzerinde ivmenin a¯ görünümünün bilinen yasasıdır. Bu önemli formül kuvvetin momentum yasasını türetmemizi sağlar. a¯'nin oranın (v¯'nin değişim oranı) zamana göre türevi olduğuna dikkat edin, bunun anlamı:

F¯ = m*dv¯/dt veya F¯*dt = m*dv¯ =>

F¯*dt = dp¯, burada dp¯ = m*dv¯

İkinci satırdaki ilk formül, kuvvetin dürtüsüdür, yani kuvvetin ürününe eşit değer ve vücuda etki ettiği zaman aralığıdır. Newton/saniye cinsinden ölçülür.

Formül Analizi

Bir önceki paragrafta yer alan kuvvet itkisi ifadesi, bu niceliğin fiziksel anlamını da ortaya koymaktadır: dt süresi boyunca hareket miktarının ne kadar değiştiğini gösterir. Bu değişikliğin (dp¯) cismin toplam momentumundan tamamen bağımsız olduğuna dikkat edin. Kuvvet dürtüsü, momentumda bir değişikliğin nedenidir, bu da hem ikincisinde bir artışa (F¯ kuvveti ile v¯ arasındaki açı 90 o'dan az olduğunda) hem de azalmasına (açı) yol açabilir. F¯ ve v¯ arasındaki değer 90 o'dan büyüktür).

Formülün analizinden önemli bir sonuç çıkar: kuvvet dürtüsünün ölçüm birimleri p¯ (saniyede newton ve saniyede metre başına kilogram) ile aynıdır, ayrıca ilk değer değişime eşittir bu nedenle ikincisinde, kuvvet dürtüsü yerine genellikle "vücut dürtüsü" ifadesi kullanılır, ancak "momentumdaki değişiklik" demek daha doğru olur.

Zamana bağlı olan ve olmayan kuvvetler

Yukarıda, kuvvet dürtü yasası diferansiyel biçimde sunuldu. Bu niceliğin değerini hesaplamak için eylem süresi üzerinden integral almak gerekir. Sonra formülü elde ederiz:

∫ t1 t2 F¯(t)*dt = Δp¯

Burada Δt = t2-t1 süresi boyunca F¯(t) kuvveti cisme etki eder, bu da momentumda Δp¯ kadar bir değişikliğe yol açar. Gördüğünüz gibi, bir kuvvetin itmesi, zamana bağlı olarak kuvvet tarafından belirlenen bir niceliktir.

Şimdi, bir dizi deneysel durumda gerçekleşen daha basit bir durumu ele alalım: kuvvetin zamana bağlı olmadığını varsayarsak, o zaman kolayca integral alabilir ve basit bir formül elde edebiliriz:

F¯*∫ t1 t2 dt = Δp¯ ​​​​=> F¯*(t2-t1) = Δp¯

Momentumun değiştirilmesiyle ilgili gerçek problemler çözülürken, kuvvetin genellikle etki süresine bağlı olmasına rağmen, sabit olduğu varsayılır ve bazı etkin ortalama değer F¯ hesaplanır.

Bir güç dürtüsünün pratikte tezahürüne örnekler

Bu değerin hangi rolü oynadığı, uygulamadan belirli örneklerle anlaşılması en kolay olanıdır. Onları vermeden önce, ilgili formülü bir kez daha yazıyoruz:

Δp¯ sabit bir değer ise, kuvvetin momentum modülü de sabittir, yani Δt ne kadar büyükse, F¯ o kadar küçüktür ve tersi de geçerlidir.

Şimdi eylem halindeki kuvvet momentumunun somut örneklerini verelim:

• Herhangi bir yükseklikten yere atlayan bir kişi, yere inerken dizlerini bükmeye çalışır, böylece zemin yüzeyinin çarpma süresini Δt arttırır (desteğin F¯ tepki kuvveti), dolayısıyla gücünü azaltır.
• Başını darbeden saptıran boksör, rakibin eldiveninin yüzüyle temas süresini Δt uzatarak darbe kuvvetini azaltır.
• Modern arabalar, bir çarpışma durumunda gövdeleri olabildiğince deforme olacak şekilde tasarlamaya çalışıyor (deformasyon, zamanla gelişen ve çarpışma kuvvetinde önemli bir azalmaya yol açan bir süreçtir ve sonuç olarak, yolcuların yaralanma riskinde azalma).

Kuvvet momenti kavramı ve momentumu

Ve bu anın dürtüsü, yukarıda ele alınanlardan farklı diğer niceliklerdir, çünkü bunlar artık doğrusal hareketle değil, dönme hareketiyle ilgilidir. Bu nedenle, M¯ kuvvet momenti, omzun vektör ürünü (dönme ekseninden kuvvetin etki noktasına olan mesafe) ve kuvvetin kendisinin, yani formül geçerlidir:

Kuvvet momenti, ikincisinin sistemin eksen etrafında burulmasını gerçekleştirme yeteneğini yansıtır. Örneğin, anahtarı somundan uzakta tutarsanız (büyük d¯ kolu), somunu sökmenizi sağlayacak büyük bir M¯ momenti oluşturabilirsiniz.

Doğrusal duruma benzeterek, M¯ momentumu, dönen bir sistem üzerinde hareket ettiği zaman aralığı ile çarpılarak elde edilebilir, yani:

ΔL¯ miktarına açısal momentumdaki değişiklik veya açısal momentum denir. Son denklem, dönme ekseni olan sistemleri ele almak için önemlidir, çünkü matematiksel olarak aşağıdaki gibi yazılan M¯ momentini yaratan hiçbir dış kuvvet yoksa sistemin açısal momentumunun korunacağını gösterir:

M¯= 0 ise L¯ = sabit

Böylece, her iki momentum denklemi (doğrusal ve dairesel hareket için), fiziksel anlamları ve matematiksel sonuçları açısından benzer görünmektedir.

Kuş ve Uçak Çarpışma Mücadelesi

Bu sorun fantastik bir şey değil. Bu tür çarpışmalar oldukça sık meydana gelir. Bu nedenle, bazı verilere göre, 1972'de İsrail hava sahasında (en yoğun kuş göçünün olduğu bölge) savaş ve nakliye uçaklarının yanı sıra helikopterlerle yaklaşık 2,5 bin kuş çarpışması kaydedildi.

Görev şu şekildedir: Yolu üzerinde v = 800 km / s hızında uçan bir uçakla karşılaşılırsa, bir kuşa hangi çarpma kuvvetinin düştüğünü yaklaşık olarak hesaplamak gerekir.

Çözüme geçmeden önce uçmakta olan kuşun uzunluğunun l = 0,5 metre ve kütlesinin m = 4 kg olduğunu varsayalım (örneğin, erkek ördek veya kaz olabilir).

Kuşun hızını (uçağınkine kıyasla küçük) ihmal edeceğiz ve ayrıca uçağın kütlesinin kuşlarınkinden çok daha büyük olduğunu kabul edeceğiz. Bu yaklaşımlar, kuşun momentumundaki değişimin şuna eşit olduğunu söylememizi sağlar:

Darbe kuvveti F'yi hesaplamak için, bu olayın süresini bilmeniz gerekir, yaklaşık olarak şuna eşittir:

Bu iki formülü birleştirerek istenen ifadeyi elde ederiz:

F \u003d Δp / Δt \u003d m * v 2 / l.

Sorunun durumundaki sayıları yerine koyarsak, F = 395062 N elde ederiz.

Vücut ağırlığı formülünü kullanarak bu rakamı eşdeğer bir kütleye çevirmek daha görsel olacaktır. O zaman şunu elde ederiz: F = 395062/9,81 ≈ 40 ton! Yani bir kuş, bir uçakla çarpışmayı sanki üzerine 40 ton yük düşmüş gibi algılar.

Klasik mekanikte hareket eden cisimlerle ilgili herhangi bir problem, momentum kavramının bilgisini gerektirir. Bu makale bu kavramı ele almakta, cismin momentum vektörünün nereye yöneldiği sorusuna cevap vermekte ve aynı zamanda problemin çözümüne ilişkin bir örnek sunmaktadır.

hareket sayısı

Vücudun momentum vektörünün nereye yönlendirildiğini bulmak için öncelikle fiziksel anlamını anlamak gerekir. Terim ilk olarak Isaac Newton tarafından açıklanmıştı ancak İtalyan bilim adamı Galileo Galilei'nin de benzer bir kavramı eserlerinde zaten kullandığını belirtmekte fayda var. Hareket eden bir nesneyi karakterize etmek için, aspirasyon, saldırı veya dürtü (İtalyanca impeto) olarak adlandırılan bir niceliği tanıttı. Isaac Newton'un değeri, bu özelliği vücuda etki eden kuvvetlerle ilişkilendirebilmesinde yatmaktadır.

Yani başlangıçta ve daha doğrusu, çoğu insanın cismin momentumundan anladığı şeye momentum diyoruz. Aslında, dikkate alınan miktarın matematiksel formülü şu şekilde yazılmıştır:

Burada m cismin kütlesi, v¯ hızıdır. Formülden de anlaşılacağı gibi herhangi bir dürtüden bahsetmiyoruz, sadece cismin hızı ve kütlesi yani hareket miktarı var.

Bu formülün matematiksel kanıtlardan veya ifadelerden kaynaklanmadığına dikkat etmek önemlidir. Fizikte ortaya çıkışı, yalnızca sezgisel, günlük bir karaktere sahiptir. Bu nedenle, herhangi bir kişi, bir sinek ve bir kamyon aynı hızda hareket ederse, bir böcekten çok daha fazla harekete sahip olduğu için kamyonu durdurmanın çok daha zor olduğunun farkındadır.

Vücudun momentum vektörü kavramının kökeni aşağıda tartışılmaktadır.

Kuvvetin dürtüsü, momentumdaki değişimin nedenidir.

Newton, sezgisel olarak tanıtılan özelliği, soyadını taşıyan ikinci yasa ile ilişkilendirmeyi başardı.

Kuvvetin dürtüsü, eylem anında herhangi bir cisme uygulanan dış kuvvetin ürününe eşit olan bilinen bir fiziksel niceliktir. Meşhur Newton yasasını kullanarak ve kuvvetin zamana bağlı olmadığını varsayarak şu ifadeye ulaşabiliriz:

F¯ * Δt = m * a¯ * Δt.

Burada Δt, F kuvvetinin etki süresidir, a, F kuvvetinin m kütleli bir cisme verdiği doğrusal ivmedir. Bildiğiniz gibi, bir cismin ivmesini hareket ettiği süre ile çarpmak, hızda bir artış verir. Bu gerçek, yukarıdaki formülü biraz farklı bir biçimde yeniden yazmamızı sağlar:

F¯ * Δt = m * Δv¯, burada Δv¯= a¯ * Δt.

Denklemin sağ tarafı momentumdaki değişimi temsil eder (önceki paragraftaki ifadeye bakın). Sonra ortaya çıkacak:

F¯ * Δt = Δp¯, burada Δp¯ = m * Δv¯.

Böylece, Newton yasasını ve bir kuvvetin momentumu kavramını kullanarak, önemli bir sonuca varılabilir: bir dış kuvvetin bir nesne üzerindeki etkisi, nesnenin momentumunda bir değişikliğe yol açar.

Şimdi, hareket miktarına neden genellikle dürtü denildiği açık hale geliyor, çünkü değişikliği kuvvetin momentumuyla çakışıyor ("kuvvet" kelimesi kural olarak atlanmıştır).

vektör miktarı p¯

Bazı niceliklerin (F¯, v¯, a¯, p¯) üzerinde bir çubuk bulunur. Bu, bir vektör özelliğinden bahsettiğimiz anlamına gelir. Yani mutlak değere (modül) ek olarak hareket miktarı, hız, kuvvet ve ivme de yön ile tanımlanır.

Her vektör ayrı bileşenlere ayrılabileceğinden, Kartezyen dikdörtgen koordinat sistemini kullanarak aşağıdaki eşitlikleri yazabiliriz:

1) p¯ = m * v¯;

2) p x \u003d m * v x; p y = m * v y ; p z = m * v z ;

3) |p¯| = √(p x 2 + p y 2 + p z 2).

Burada, 1. ifade momentum temsilinin vektör formudur, 2. formül seti, karşılık gelen hız bileşenlerini (x, y, z endeksleri vektörün izdüşümünü gösterir) bilerek momentum bileşenlerinin her birini p¯ hesaplamanıza izin verir. karşılık gelen koordinat ekseni). Son olarak, 3. formül, bileşenleri aracılığıyla momentum vektörünün uzunluğunu (miktarın mutlak değeri) hesaplamanıza olanak tanır.

Vücudun momentum vektörü nereye yönlendirilir?

Momentum p¯ kavramını ve temel özelliklerini göz önünde bulundurarak, sorulan soruya kolayca cevap verilebilir. Vücudun momentum vektörü, doğrusal hız vektörü ile aynı şekilde yönlendirilir. Aslında, a¯ vektörünün k sayısı ile çarpılmasının, aşağıdaki özelliklere sahip yeni bir b¯ vektörünün oluşumuna yol açtığı matematikten bilinmektedir:

• uzunluğu, sayının ürününe ve orijinal vektörün modülüne eşittir, yani |b¯| = k * |a¯|;
• k > 0 ise orijinal vektörle aynı şekilde yönlendirilir, aksi takdirde a¯'nin tersine yönlendirilir.

Bu durumda a¯ vektörünün rolü v¯ hızı tarafından oynanır, momentum p¯ yeni vektör b¯ ve k sayısı cismin kütlesi m'dir. İkincisi her zaman pozitif (m>0) olduğu için, şu soruyu yanıtlayarak: p¯ cismi momentum vektörünün yönü nedir, bunun v¯ hızına eş-yönlü olduğu söylenmelidir.

Momentum değişim vektörü

Başka bir benzer soruyu düşünmek ilginçtir: Vücudun momentumundaki değişim vektörü, yani Δp¯ nereye yönlendirilir. Cevaplamak için yukarıda elde edilen formülü kullanmalısınız:

F¯ * Δt = m * Δv¯ = Δp¯.

Bir önceki paragraftaki mantığa dayanarak, momentumdaki değişim yönünün Δp¯ kuvvet vektörünün F¯ (Δt > 0) yönüyle veya hızdaki değişim vektörünün yönü Δv¯ ile çakıştığını söyleyebiliriz ( m > 0).

Değerlerdeki bir değişiklikten bahsettiğimizi burada karıştırmamak önemlidir. Genel olarak, p¯ ve Δp¯ vektörleri birbirleriyle hiçbir şekilde ilişkili olmadıkları için çakışmazlar. Örneğin, F¯ kuvveti cismin v¯ hızına etki edecekse, o zaman p¯ ve Δp¯ zıt yönlere yönlendirilecektir.

Momentumun vektör doğasını hesaba katmak nerede önemlidir?

Yukarıda tartışılan sorular: cismin momentum vektörünün ve değişim vektörünün nereye yönlendirildiği, basit meraktan kaynaklanmaz. Buradaki nokta, momentum korunum yasasının p¯ bileşenlerinin her biri için geçerli olmasıdır. Yani en eksiksiz haliyle şu şekilde yazılmıştır:

p x = m * v x ; p y = m * v y ; p z = m * v z .

p¯ vektörünün her bileşeni, dış kuvvetlerden etkilenmeyen etkileşimli nesneler sisteminde değerini korur (Δp¯ = 0).

Cisimlerin etkileşimi (çarpışma) ile ilgili problemleri çözmek için p¯'nin bu kanunu ve vektör temsilleri nasıl kullanılır?

İki top sorunu

Aşağıdaki şekilde yatay bir çizgi üzerinde farklı açılarda uçan farklı kütlelere sahip iki top gösterilmektedir. Topların kütleleri m 1 = 1 kg, m 2 = 0,5 kg, hızları v 1 = 2 m/s, v 2 = 3 m/s olsun. Topların çarpmasından sonraki momentumun yönünü, topların kesinlikle esnek olmadığını varsayarak belirlemek gerekir.

Problemi çözmeye başlayarak, momentumun değişmezliği yasasını vektör biçiminde yazmalıyız, yani:

p 1 ¯ + p 2 ¯ = sabit.

Her bir momentum bileşeninin korunması gerektiğinden, çarpışmadan sonra iki topun tek bir nesne olarak hareket etmeye başlayacağı (tamamen elastik olmayan etki) dikkate alınarak bu ifade yeniden yazılmalıdır:

m 1 * v 1x + m 2 * v 2x = (m 1 + m 2) * u x ;

M 1 * v 1y + m 2 * v 2y = (m 1 + m 2) * sen y .

Birinci cismin momentumunun y eksenine izdüşümü için eksi işareti, y ekseninin seçilen vektörüne karşı yönü nedeniyle ortaya çıktı (bkz. Şekil).

Şimdi u hızının bilinmeyen bileşenlerini ifade etmemiz ve ardından bilinen değerleri ifadelere koymamız gerekiyor (hızların karşılık gelen projeksiyonları, v 1 ¯ ve v 2 ¯ vektörlerinin modüllerinin trigonometrik fonksiyonlarla çarpılmasıyla belirlenir. ):

u x = (m 1 * v 1x + m 2 * v 2x) / (m 1 + m 2), v 1x = v 1 * cos(45 o); v 2x = v 2 * cos(30o);

u x \u003d (1 * 2 * 0,7071 + 0,5 * 3 * 0,866) / (1 + 0,5) \u003d 1,8088 m / s;

u y = (-m 1 * v 1y + m 2 * v 2y) / (m 1 + m 2), v 1y = v 1 * sin(45 o); v 2y = v 2 * sin(30o);

u y = (-1 * 2 * 0,7071 + 0,5 * 3 * 0,5) / (1 + 0,5) = -0,4428 m/s.

Bunlar, topların çarpması ve "yapışması" sonrasında vücudun hızının iki bileşenidir. Hızın yönü momentum vektörü p¯ ile çakıştığı için, u¯'yi tanımlarsak problemin sorusu cevaplanabilir. Yatay eksene göre açısı, u y ve u x bileşenlerinin oranının yay tanjantına eşit olacaktır:

α \u003d arktg (-0,4428 / 1,8088) \u003d -13,756 o.

Eksi işareti, darbeden sonraki momentumun (hızın) x ekseninden aşağı doğru yönlendirileceğini gösterir.