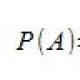Раздели на сайта
Избор на редакторите:
- Удостоверение за завършване на неделното училище (Toosh).
- Свети доктор-мъченик Евгений Боткин
- Страстоносец Евгений Боткин
- Как да се отървете от безпокойство, страх и тревога
- Какво представлява "наполеоновият комплекс" синдром на Наполеон в мъжката психология
- Евгени Боткин
- Женски глас: класификация, най-нисък и най-висок женски глас
- Как се променя животът след преживяването на просветление (пробуждане)?
- Основните точки на тестване
- Как да се отървете от страха от смъртта: съвети и психотерапевтична помощ
Реклама
| Теореми за абсорбция, залепване и де Морган. Размити и произволни множества Основни еквивалентности на пропозиционалната алгебра |
|
Асоциативност x 1 (x 2 x 3) = (x 1 x 2) x 3; x 1 Ú (x 2 Ú x 3) = (x 1 Ú x 2) Ú x 3. Комутативност x 1 x 2 = x 2 x 1 x 1 Ú x 2 = x 2 Ú x 1 Дистрибутивност на конюнкция спрямо дизюнкция x 1 (x 2 Ú x 3) = x 1 x 2 Ú x 1 x 3. Дистрибутивност на дизюнкция спрямо конюнкция x 1 Ú (x 2 × x 3) = (x 1 Úx 2) × (x 1 Úx 3). * Идемпотентност (тавтология) Два пъти не Постоянни свойства x & 1 = x; (закони на универсалния набор) x & 0 = 0; (нулеви закони) Правилата на Де Морган (закони)
Закон за противоречието (допълняемостта). Трети (комплементарност) закон за изключване Доказателствата на всички тези формули са тривиални. Една от възможностите е да изградите таблици на истинността за лявата и дясната страна и да ги сравните. Правила за свързване Правилото за залепване за елементарни конюнкции следва от закона за разпределението, закона за допълването и закона за универсалното множество: дизюнкция на два съседни съюза може да бъде заменена с единичен елементарен съюз, който е обща част от оригиналните съюзи . Правилото за слепване за елементарни суми следва от закона за разпределението от втория вид, закона за допълването и закона за нулевото множество: съюзът на две съседни клаузи може да бъде заменен с една елементарна клауза, която е общата част на оригиналните клаузи . Правило за усвояване Правилото за поглъщане за сумата от два елементарни произведения следва от закона за разпределението от първия вид и законите на универсалното множество: дизюнкция от две елементарни конюнкции, от които едната е неразделна част от другата, може да бъде заменена с конюнкция с по-малък брой операнди . Правилото на абсорбция за произведението на елементарните суми следва от закона за разпределението от втория вид и законите на нулевия набор: конюнкцията на две елементарни дизюнкции, едната от които е неразделна част от другата, може да бъде заменена с елементарна дизюнкция с по-малък брой операнди. Правило за внедряване Това правило определя обратното действие на залепването. Правилото за разширяване на елементарно произведение в логическа сума от елементарни произведения от по-висок ранг (до r = n, т.е. до съставните части на единица, както ще бъде обсъдено по-долу) следва от законите на универсалното множество, разпределението закон от първи вид и се изпълнява на три етапа: В разширяемото елементарно произведение на ранг r той се въвежда като фактори на n-r единици, където n е рангът на съставната част на единица; Всяка единица се заменя с логическата сума на някаква променлива, която не присъства в оригиналния елементарен продукт и неговото отрицание: x i v `x i = 1; Всички скоби се отварят на базата на закона за разпределението от първи вид, което води до разширяване на първоначалното елементарно произведение от ранг r в логическа сума от 2 n-r съставни части на единицата. Правилото за разгъване на елементарния продукт се използва за минимизиране на функциите на булевата алгебра (FAL). Правилото за разширяване на елементарна сума от ранг r до произведението на елементарни суми от ранг n (компоненти на нула) следва техните закони за нулевия набор (6) и закона за разпределението от втория вид (14) и се изпълнява в три етапи: В разширяемата сума от ранг r, n-r нули се въвеждат като членове; Всяка нула е представена като логически продукт на някаква променлива, която не присъства в първоначалната сума и нейното отрицание: x i·` x i = 0; Полученият израз се трансформира въз основа на закона за разпределението от втори вид (14), така че първоначалната сума от ранг r се разгръща в логически продукт от 2 n-r съставни части на нула. 16. Концепцията за цялостна система. Примери за цялостни системи (с доказателство) Определение.Набор от булеви функции A се нарича пълна система (в P2), ако някоя булева функция може да бъде изразена с формула над A. Система от функции A = ( f 1, f 1, ..., f m), който е пълен се нарича основа. Минимална основа е база, за която е премахната поне една функция е 1формирайки тази основа, трансформира системата от функции (f 1, f 1, ..., f m)непълна. Теорема.Системата A = (∨, &,) е пълна. Доказателство. Ако функцията на алгебрата на логиката f е различна от идентичната нула, тогава f се изразява под формата на перфектна дизюнктивна нормална форма, която включва само дизюнкция, конюнкция и отрицание. Ако f ≡ 0, тогава f = x & x. Теоремата е доказана. Лема.Ако система A е пълна и всяка функция на система A може да бъде изразена с формула върху някаква друга система B, тогава B също е пълна система. Доказателство. Да разгледаме произволна булева функция f (x 1,…, x n) и две системи от функции: A = (g 1, g 2,…) и B = (h 1, h 2,…). Тъй като системата A е пълна, функцията f може да бъде изразена като формула над нея: f (x 1,…, x n) = ℑ където g i = ℜ i т.е. функцията f се представя като f (x 1,…, x n) = ℑ [ℜ1, ℜ2, ...] с други думи, тя може да бъде представена с формула над B. Преминавайки през всички функции на булевата алгебра по този начин, получаваме, че системата B също е пълна. Лемата е доказана. Теорема.Следните системи са завършени в P 2: 4) (&, ⊕, 1) основа на Жегалкин. Доказателство. 1) Известно е (теорема 3), че системата A = (&, V,) е пълна. Нека покажем, че системата B = (V, е пълна. Всъщност от закона на де Морган (x & y) = (x ∨ y) получаваме, че x & y = (x ∨ y), т.е. конюнкцията е изразено чрез дизюнкция и отрицание, а всички функции на система A се изразяват с формули върху система B. Според лемата, система B е пълна. 2) Подобно на т. 1: (x ∨ y) = x & y ⇔ x ∨ y = (x & y) и лема 2 предполага истинността на точка 2. 3) х | y = (x & y), x | х = х; x & y = (x | y) = (x | y) | (x | y) и съгласно лема 2 системата е пълна. 4) x = x ⊕1 и съгласно лема 2 системата е пълна. Теоремата е доказана. 17. Алгебрата на Жегалкин. Свойства и пълнота на операцията Наборът от булеви функции, дефинирани в основата на Жегалкин S4 = (⊕, &, 1), се нарича Алгебра на Жегалкин. Основни свойства. 1. коммутируемост h1⊕h2 = h2⊕h1 h1 & h2 = h2 & h1 2. асоциативност h1⊕ (h2⊕h3) = (h1⊕h2) ⊕h3 h1 & (h2 & h3) = (h1 & h2) & h3 3. дистрибутивност h1 & (h2⊕h3) = (h1 & h2) ⊕ (h1 & h3) 4. свойства на константите 5.h⊕h = 0 h & h = h x → y = 1⊕x⊕xy x ↓ y = 1⊕x⊕y⊕xy 18. Полином Жегалкина. Строителни методи. Пример. Полиномът на Жегалкин (полином по модул 2) в нпроменливите x 1, x 2 ... x n се нарича израз от вида: c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n, където константите C k могат да приемат стойности 0 или 1. Ако полиномът на Жегалкин не съдържа произведения на отделни променливи, тогава той се нарича линеен (линейна функция). Например, f = x⊕yz⊕xyz и f 1 = 1⊕x⊕y⊕z са полиноми, а втората е линейна функция. Теорема... Всяка булева функция е уникално представена като полином на Жегалкин. Ето основните методи за конструиране на полиноми на Жегалкин в дадена функция. 1. Методът на недефинираните коефициенти. Нека P (x 1, x 2 ... x n) е необходимият полином на Жегалкин, реализиращ дадена функция f (x 1, x 2 ... x n). Нека го запишем във формата P = c 0 ⊕c 1 x 1 ⊕c 2 x 2 ⊕ ... ⊕c n x n ⊕c 12 x 1 x 2 ⊕ ... ⊕c 12 ... n x 1 x 2 ... x n Намерете коефициентите C k. За да направите това, ние последователно присвояваме променливите x 1, x 2 ... x n стойности от всеки ред на таблицата на истината. В резултат на това получаваме система от 2 n уравнения с 2 n неизвестни, която има уникално решение. След като го решим, намираме коефициентите на полинома P (X 1, X 2 ... X n). 2. Метод, базиран на трансформиране на формули върху набор от съединителни (, &). Създайте някаква формула Фнад множеството съединителни (, &), реализиращи дадената функция f (X 1, X 2 ... X n). След това навсякъде заменете подформулите от формата A с A⊕1, разширете скобите, използвайки разпределителния закон (вижте свойство 3) и след това приложете свойства 4 и 5. Пример... Построете полинома на Жегалкин на функцията f (X, Y) = X → Y Решение. P = c 0 ⊕c 1 x⊕c 2 y⊕c 12 xy Използвайки таблицата на истинността на импликацията, намираме това f (0,0) = P (0,0) = C 0 = 1 f (0,1) = P (0,1) = C 0 ⊕C 2 = 1 f (1,0) = P (1,0) = C 0 ⊕C 1 = 0 f (1,1) = P (1,1) = C 0 ⊕C 1 ⊕C 2 ⊕C 12 = 1 Откъдето последователно намираме C 0 = 1, C 1 = 1, C 2 = 0, C 12 = 1 Следователно: x → y = 1⊕X⊕XY. 2. (Метод на преобразуване на формули.). Имаме: x → y = xvy = (xy) = (x (y⊕1)) ⊕1 = 1⊕x⊕xy Подобна информация. Разглежданите операции върху множества са подчинени на определени закони, които наподобяват добре познатите елементарни закони на алгебрата на числата. Това определя името набор алгебра, която често се нарича булева алгебра на множествата, което се свързва с името на английския математик Джон Бул, който основава своите логически изследвания върху идеята за аналогия между алгебрата и логиката. За произволни множества A, B и C са валидни следните идентичности (Таблица 3.1): Таблица 3.1
Законите на алгебрата на множествата по отношение на операциите на пресичане () и обединение () се подчиняват на принципа на двойствеността: ако във всеки закон всички знаци за пресичане се заменят със знаци за обединение, а всички знаци на обединение със знаци за пресичане, знакът на вселената (U) се заменя със знака за празно множество (Ø), а празният знак е знакът на вселената, тогава отново получаваме правилната идентичност. Например (по силата на този принцип) следва от и т.н. 3.1. Тестване на истинността на идентичностите с помощта на диаграми на Ойлер-ВенВсички закони на алгебрата на множествата могат да бъдат визуализирани и доказани с помощта на диаграми на Ойлер-Вен. Това изисква: Начертайте съответната диаграма и засенчете всички множества от лявата страна на равенството. Начертайте друга диаграма и направете същото за дясната страна на уравнението. Тази идентичност е вярна, ако и само ако една и съща област е засенчена и на двете диаграми. Забележка 3.1.Две пресичащи се окръжности разделят целия универсален набор на четири области (виж фигура 3.1)
 Забележка 3.2.Три пресичащи се кръга разделят целия универсален набор на осем региона (виж фигура 3.2):  Забележка 3.2.При записване на условията на различни примери често се използва нотацията: - от ... следва ...; - ако и само ако…. Задача 3.1 ... Опростете изразите за алгебра на набора:  Решение. 
Задача 3 .2 ... Докажете самоличности: (AB) \ B = A \ B; A (BC) = A \ (A \ B) (A \ C). Решение. 
Задача 3.3 ... Докажете следните отношения по два начина: с помощта на диаграми и с помощта на определението за равенство на множествата.  Решение. 
2. Доказателство с помощта на определението за равенство на множествата. По дефиниция множествата X и Y са равни, ако следните отношения са изпълнени едновременно: XY и YX. Нека първо покажем това Сега нека докажем обратното, тоест означава, A (BC) = (AB) (AC); 1. Доказателство чрез диаграма:
Нека бъде NSА (ВС). Тогава NSА и NSВС. Ако NSВ, тогава NSАВ, което не противоречи на казаното, което означава, че NS (АВ) (АС). Ако NSС, тогава NSАС. следователно, NS (AB) (AC). И така, доказахме, че A (BC) (AB) (AC. Нека сега NS (AB) (AC). Ако NSАВ, значи NSА и NSV. Оттук следва, че NSА и NSВС, т.е NSА (ВС). Ако NSАС, значи NSА и NSC. Оттук следва, че NSА и NSВС, т.е NSА (ВС). Така (AB) (AC) A (BC). Следователно A (BC) = (AB) (AC). Q.E.D.
При доказване на достатъчността получихме, че AB = . Очевидно C, така че връзката е доказана. При доказването беше разгледан най-общият случай. Тук обаче са възможни още някои опции при конструиране на диаграми. Например случай на равенство АВ = С или 2. Доказателство с помощта на определението за равенство на множествата. Трябва. Нека АВС и елемента NSА. Нека покажем, че в този случай елемент от множеството A също ще бъде елемент от множеството Помислете за два случая: NSB или Ако NSВ, тогава NSАВС, т.е NSС и в резултат на това, Ако Нека сега Ако NSАВ, значи NSА и NSV. Дотолкова доколкото  1. Доказателство чрез диаграма:
2. Доказателство с помощта на определението за равенство на множествата. Нека AB. Помислете за елемента NSВ (или Задача 3.4. Изразете обозначените области символично и опростете получените изрази.
Решение. Зоната за търсене се състои от две изолирани части. Да ги наречем отгоре и отдолу. Множеството, което те представляват, може да се опише по следния начин: M = ( х хА и NSB и NSC или NSC и NSA и NSБ). От дефиницията на операциите върху множествата получаваме: M = ((AB) \ C) (C \ A \ B). Нека напишем този израз, използвайки основни операции - допълнение, обединение и пресичане: Невъзможно е да се опрости този израз, тъй като имаме едно срещане на всеки символ. Това е най-простата форма на тази формула. Тази област може да се разглежда като обединение на множествата A \ B \ C и ABC. По дефиниция M = ( х хА и хB и NSC или NSА и NSB и NSC). Нека опростим: Задачи за самостоятелно решение. 1. Опростете: 2. Докажете с помощта на диаграми, закони на алгебрата на множествата и дефиниция на равенството на множествата: (AB) \ B = A \ B; A (BC) = A \ (A \ B) (A \ C); АВ = АВ А = В; A \ B = AB = A. 3. Разберете дали има множество X, удовлетворяващо за всяко A равенството: AX = A; (отговор );
|
Законите на Де Морган са логически правила, установени от шотландския математик Август де Морган, които свързват двойки логически операции с помощта на логическо отрицание. Август де Морган отбеляза, че в класическата логика са верни следните отношения: не (A и B) = (не A) или (не B) не (A или B) = (не A) и (не B) В по-позната за нас форма тези съотношения могат да бъдат записани в следната форма: Законите на Де Морган могат да бъдат формулирани по следния начин: Аз закон на Морган:Отричането на дизюнкция на две прости твърдения е равносилно на свързване на отрицанията на тези твърдения. Законът на II де Морган:Отричането на свързването на две прости твърдения е равносилно на разделянето на отрицанията на тези твърдения. Нека разгледаме прилагането на законите на Де Морган с конкретни примери. Пример 1.Трансформирайте формулата, така че да няма отрицания на сложни твърдения. Използвайки първия закон на дьо Морган получаваме: за да отречем връзката на прости твърдения B и C, прилагаме втория закон на дьо Морган, получаваме:
поради това:
В резултат на това получихме еквивалентно твърдение, в което няма отричане на съставни твърдения и всички отрицания се отнасят само до прости твърдения. Можете да проверите валидността на решението с помощта на таблици за истинност. За да направим това, ще съставим таблици на истинността за оригиналното твърдение: и за твърдение, получено в резултат на трансформации, извършени с помощта на законите на де Морган:
Маса 1.
Както можете да видите от таблиците, оригиналното логическо изявление и логическото твърдение, получено с помощта на законите на де Морган, са еквивалентни. Това се доказва от факта, че в таблиците на истината получихме едни и същи набори от стойности. Формули и закони на логикатаВъв встъпителен урок по основите на математическата логика, запознахме се с основните понятия на този раздел от математиката и сега темата естествено се продължава. В допълнение към нов теоретичен, или по-скоро дори не теоретичен, а общообразователен материал, ни очакват практически задачи и следователно, ако сте влезли в тази страница от търсачка и / или сте зле ориентирани в материала, моля, следвайте горната връзка и започнете с предишната статия. Освен това за практика ни трябват 5 таблици на истината логически операциикоето и горещо препоръчвам пренаписване на ръка. НЕ помнете, НЕ печатайте, а именно, да разберете отново и да пренапишете на хартия със собствената си ръка - така че да са пред очите ви: - масата НЕ Е; Много е важно. По принцип би било удобно да ги номерирате. "Таблица 1", "Таблица 2" и т.н., но многократно съм подчертавал недостатъка на този подход - както се казва, в единия източник таблицата ще бъде първа, а в другия - сто и първата. Затова ще използваме „естествени“ имена. Продължаваме: Всъщност вече сте запознати с концепцията за логическа формула. Ще ви дам стандартен, но доста остроумен определение: формулиалгебрите на изявленията се наричат: 1) всякакви елементарни (прости) твърдения; 2) ако и са формули, тогава формулите също са изрази на формата Няма други формули. По-специално, формула е всяка логическа операция, като логическото умножение. Обърнете внимание на втората точка - тя позволява рекурсивенначин за "създаване" на произволно дълга формула. Дотолкова доколкото Формула неима например запис - и тук е очевидна аналогия с "алгебрични боклуци", от които не става ясно дали числата трябва да се събират или умножават. Логическата формула може да се разглежда като логическа функция... Нека запишем същия съюз във функционална форма: В този случай елементарните изрази също играят ролята на аргументи (независими променливи), които в класическата логика могат да приемат 2 стойности: вярноили Лъжа... В това, което следва, за удобство понякога ще се позовавам на прости твърдения променливи. Таблицата, описваща логическата формула (функция), се нарича, както вече беше обявено, таблица на истината... Моля - позната снимка: Трябва да кажа, че "изходът" тук се оказа "в една стъпка", но в общия случай логическата формула е по-сложна. И в такива "трудни случаи" трябва да наблюдавате ред на изпълнение на логически операции: - първо се извършва отрицание; Така, например, нотацията предполага, че първо трябва да извършите логическо умножение, а след това - логическо събиране:. Точно както в „обикновената“ алгебра – „първо умножаваме, а след това събираме“. Редът на действията може да се промени по обичайния начин - със скоби: Сигурно всеки разбира, но за всеки пожарникар: и този две различниформули! (както формално, така и по същество) Нека съставим таблица на истинността за формулата. Тази формула включва две елементарни твърдения и "на входа" трябва да изброим всички възможни комбинации от единици и нули. За да избегнем объркване и недоразумения, ние сме съгласни да изброим комбинации строго в този ред (което всъщност използвам де факто от самото начало): (трите хоризонтални ленти са иконата на самоличността) В първата част на урока обещах да изразя внушението чрез основни логически операции и изпълнението на обещанието не закъсня! Желаещите могат да вложат смислен смисъл в импликацията (например „Ако вали, навън е влажно“)и независимо анализирайте еквивалентното твърдение. Да формулираме обща дефиниция: двете формули се извикват еквивалент (идентичен)ако приемат едни и същи стойности за всеки набор от стойности, включени в тези формули от променливи (елементарни твърдения)... Също така се казва, че "Формулите са еквивалентни, ако техните таблици за истинност съвпадат"но тази фраза наистина не ми харесва. Упражнение 1 Начертайте таблица на истинността за формулата и се уверете, че самоличността, която знаете, е вярна. Нека повторим реда на решаване на проблема още веднъж: 1) Тъй като формулата включва две променливи, ще има общо 4 възможни набора от нули и единици. Записваме ги в посочения по-горе ред. 2) Импликациите са "по-слаби" от конюнкцията, но са разположени в скоби. Попълваме колоната, като е удобно да използвате следните приложни разсъждения: "Ако нулата следва от единица, тогава поставяме нула, във всички останали случаи - едно"... След това попълваме колоната за импликацията и в същото време, Внимание!- колони и трябва да се анализират "отдясно наляво"! 3) И на последния етап попълнете последната колона. И тук е удобно да се разсъждава така: "Ако в колоните има две единици, тогава поставяме една, във всички останали случаи - нула". Накрая проверяваме таблицата на истинността еквиваленти . Основни еквивалентности на пропозиционалната алгебраТоку-що се запознахме с двама от тях, но, разбира се, въпросът не се ограничава само до тях. Има доста самоличности и ще изброя най-важните и най-известните от тях: Комутативност на конюнкция и комутативност на дизюнкцияКомутативностПроменливостта е: Правила, познати от 1. клас: „Продуктът (сумата) не се променя от пермутацията на факторите (термините)“... Но при цялата привидна елементарност на това свойство, то не винаги е вярно, по-специално е некомутативно. матрично умножение (по принцип те не могат да бъдат пренаредени), а векторно произведение на векторите- антикомутивен (пермутацията на векторите води до промяна на знака). И освен това тук отново искам да подчертая формализма на математическата логика. Така например фразите "Студентът издържа изпита и пи"и "Студентът пи и издържа изпита"различен от материална гледна точка, но неразличим от гледна точка на формалната истина. ... Всеки от нас познава такива ученици и по етични причини няма да изричаме конкретни имена =) Асоциативност на логическото умножение и събиранеИли, ако "подобно на училище" - комбинирано свойство: Разпределителни свойстваМоля, имайте предвид, че във втория случай ще бъде неправилно да се говори за „отварящи се скоби“, в известен смисъл тук е „фантастика“ - в края на краищата те могат да бъдат премахнати напълно: тъй като умножението е по-силна операция. И отново, тези на пръв поглед "банални" свойства не са изпълнени във всички алгебрични системи и освен това изискват доказателство (за което ще говорим съвсем скоро)... Между другото, вторият закон на разпределението не е валиден дори в нашата "обичайна" алгебра. И всъщност: Законът за идемпотентносттаКакво да правя, латински... Директно някакъв принцип на здравата психика: „Аз и аз съм аз“, „Аз или аз също съм аз“ =) И тогава има няколко подобни самоличности: ... хм, нещо, на което дори се закачих ... за да се събудиш с доктор по философия утре =) Законът за двойното отрицаниеЕ, тук вече се навежда пример с руския език - всеки знае отлично, че две частици "не" означават "да". И за да се засили емоционалното оцветяване на отричането, често се използват три „не“: Закони за усвояване- "Имаше ли момче?" =) В правилната идентичност скобите могат да бъдат пропуснати. Законите на Де МорганДа предположим, че строгият Учител (чието име също знаеш :))полага изпит, ако - Студентът отговори на 1-ви въпрос и – Ученикът отговори на 2-ри въпрос... След това изявлението, в което се посочва това Студент неиздържал изпита, ще бъде еквивалентно на изявлението - Студент неотговори на 1-ви въпрос илипо 2-ри въпрос. Както бе отбелязано по-горе, еквивалентностите подлежат на доказване, което се извършва по стандартен начин с помощта на таблици на истинност. Всъщност ние вече доказахме еквивалентностите, изразяващи импликация и еквивалентност, и сега е време да консолидираме техниката за решаване на този проблем. Нека докажем самоличността. Тъй като съдържа едно изявление, "на входа" са възможни само две опции: една или нула. След това присвояваме една колона и прилагаме към тях правило И: Да, това доказателство е примитивно (и някой ще каже, че "глупаво"), но типичен учител по матология ще му разтърси сърцето. Следователно дори такива прости неща не трябва да се приемат лекомислено. Сега нека се убедим, например, в валидността на закона на де Морган. Първо, нека направим таблица на истинността за лявата страна. Тъй като дизюнкцията е в скоби, първо я изпълняваме, след което отричаме колоната: Всяка еквивалентност може да бъде представена като идентично с истинската формула... Означава, че ЗА ВСЕКИ оригинален набор от нули и единици"На изхода" е строго едно. И има много просто обяснение за това: тъй като таблиците на истинността и съвпадат, тогава, разбира се, те са еквивалентни. Нека комбинираме, например, чрез еквивалент лявата и дясната страна на току-що доказаната идентичност на де Морган: Задача 2 Докажете следните еквивалентности: б) Кратко решение в края на урока. Не сме мързеливи! Опитайте не само да съставите таблици на истинността, но и ясноформулирайте заключения. Както отбелязах наскоро, пренебрегването на прости неща може да стане много, много скъпо! Продължаваме да се запознаваме със законите на логиката!Да, точно така - ние вече работим с тях с всички сили: Вярнопри е наречен идентично с истинската формулаили законът на логиката. По силата на предварително оправдания преход от еквивалентност към идентично вярна формула, всички изброени по-горе идентичности са закони на логиката. Формулата, която приема стойността лъжапри всеки набор от стойности на променливите, включени в негое наречен идентично фалшива формулаили противоречие. Собствен пример за противоречие от древните гърци: Доказателството е тривиално: Всяко противоречие обаче също е закон на логиката, по-специално: Невъзможно е да се обхване толкова обширна тема в една статия и затова ще се огранича само до още няколко закона: Законът на изключеното трето- в класическата логика всяко твърдение е вярно или невярно и няма трето. „Да бъдеш или да не бъдеш“ е въпросът. Начертайте сами табелка с истината и се уверете, че е така идентично вярноформула. Законът за противопоставянетоТози закон беше активно обсъждан, когато обсъждахме същността на необходимо условие, помня: „Ако е влажно по време на дъжд, тогава следва, че ако навън е сухо, тогава със сигурност не е валяло.. От този закон следва също, че ако е справедливо е прав теорема, след това изявлението, което понякога се нарича противоположнотеорема. Ако е вярно обратентеорема, тогава по силата на закона за противопоставянето, теоремата също е валидна, обратен обрат: И отново, обратно към нашите информативни примери: за изявления - числото се дели на 4, - числото се дели на 2справедливо прави противоположнотеореми, но неверни обратени обратен обраттеореми. За "възрастната" формулировка на Питагоровата теорема всичките 4 "посоки" са верни. Закон за силогизмаСъщо така класика на жанра: "Всички дъбове са дървета, всички дървета са растения, следователно всички дъбове са растения.". Е, тук отново бих искал да отбележа формализма на математическата логика: ако нашият строг Учител смята, че определен ученик е дъб, то от формална гледна точка този ученик определено е растение =) ... въпреки че, ако мислиш за това, тогава може би и с неформална = ) Нека съставим таблица на истинността за формулата. В съответствие с приоритета на логическите операции, ние се придържаме към следния алгоритъм: 1) изпълняваме импликациите и. Най-общо казано, можете веднага да изпълните 3-та импликация, но с нея е по-удобно (и разрешено!)разберете го малко по-късно; 2) прилага се към колони правило И; 3) сега правим; 4) и в последната стъпка прилагаме импликацията към колоните Чувствайте се свободни да контролирате процеса с показалеца и средния си пръст :)) Задача 3 Разберете дали следната формула ще бъде закон на логиката: Кратко решение в края на урока. Да, и почти забравих - нека се съгласим да изброим началните множества от нули и единици в точно същия ред, както при доказването на закона на силогизма. Разбира се, редовете могат да бъдат пренаредени, но това значително ще усложни сравнението с моето решение. Преобразуване на булеви формулиВ допълнение към тяхната "логическа" цел, еквивалентностите се използват широко за трансформиране и опростяване на формули. Грубо казано, една част от идентичността може да бъде заменена с друга. Така че, например, ако попаднете на фрагмент в логическа формула, тогава, според закона за идемпотентността, можете (и трябва) да го напишете просто вместо него. Ако виждате, тогава по закона на абсорбцията опростете въвеждането до. И т.н. Освен това има още едно важно нещо: идентичностите са валидни не само за елементарни твърдения, но и за произволни формули. Например:
Преобразуваме, например, сложното внушение След това прилагаме "комплексния" закон на де Морган към скобата, докато поради приоритета на операциите, това е законът, при който Скобите могат да се свалят като вътре има "по-силен" съюз: Е, с комутативността като цяло всичко е просто - дори не е нужно да обозначавате нищо ... законът на силогизма е потънал в душата ми за нещо :)) Така законът може да бъде пренаписан в по-сложна форма: Говорете на глас логическата верига „с дъб, дърво, растение“ и ще разберете, че смисълът на закона изобщо не се е променил от пренареждането на последиците. Може би формулировката е станала по-оригинална. Като обучение, нека опростим формулата. Откъде да започна? На първо място, за да разберем реда на действията: тук отрицанието се прилага към цялата скоба, която е „закрепена“ към твърдението чрез „малко по-слаб“ съюз. По същество имаме пред нас логичен продукт от два фактора:. От двете останали операции импликацията има най-нисък приоритет и следователно цялата формула има следната структура:. Като правило, в първата стъпка(и) човек се отървава от еквивалентността и импликацията (ако са)и свеждане на формулата до три основни логически операции. Какво можеш да кажеш…. Логично е. (1) Ние използваме самоличността Това обикновено е последвано от "демонтаж" със скоби. Първо цялото решение, след това коментарите. За да не получа "маслено масло", ще използвам иконите на "обикновеното" равенство: (2) Прилагаме закона на дьо Морган към външните скоби, където. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Прочети: |
|---|
Популярен:
Каква е равновесната константа
|
Нов
- Забележителности на Лондон на английски: описание и снимки Характеристики за описание на обекта
- Правила за добавяне
- Основни форми на поздрави (превод Nihao)
- Фразов глагол TURN, изрази и идиоми
- BelZhD има онлайн табло
- Какво е ускорение? Скорост. ускорение Тялото се ускорява, ако
- Шаблони на менюта в Word: изтегляне и отпечатване
- Проста математика на теоремата на Байес
- Корелационен критерий на Пиърсън Коефициент на корелация 1 означава
- Размити и произволни множества Основни еквивалентности на пропозиционалната алгебра



 и универсални U множества
и универсални U множества и универсални U множества
и универсални U множества



 ... Нека бъде NS- произволен елемент от множеството
... Нека бъде NS- произволен елемент от множеството  , това е NS
, това е NS ... Означава, че NSU и NS
... Означава, че NSU и NS  ... Оттук следва, че NSA или NSV. Ако NSА, тогава NSĀ, което означава
... Оттук следва, че NSA или NSV. Ако NSА, тогава NSĀ, което означава  ... Ако NSВ, тогава
... Ако NSВ, тогава  , което означава
, което означава  ... По този начин всеки елемент от комплекта.
... По този начин всеки елемент от комплекта.  ... също е елемент от комплекта
... също е елемент от комплекта  Това е
Това е 
 ... Нека бъде
... Нека бъде  ... Ако NSĀ, тогава NSU и NSA, което означава NSАВ. Оттук следва, че
... Ако NSĀ, тогава NSU и NSA, което означава NSАВ. Оттук следва, че  ... Ако
... Ако  , тогава NSU и NSV. означава, NSАВ, т.е
, тогава NSU и NSV. означава, NSАВ, т.е  ... Оттук следва, че всеки елемент от множеството
... Оттук следва, че всеки елемент от множеството  също е елемент от комплекта
също е елемент от комплекта  , това е
, това е  .
. , както се изисква за доказване.
, както се изисква за доказване.

 , случай на празни множества и т.н. Очевидно може да е трудно да се вземат предвид всички възможни опции. Поради това се смята, че доказването на отношения с помощта на диаграми не винаги е правилно.
, случай на празни множества и т.н. Очевидно може да е трудно да се вземат предвид всички възможни опции. Поради това се смята, че доказването на отношения с помощта на диаграми не винаги е правилно. .
. .
. .
. , тогава
, тогава  ... Необходимостта е доказана.
... Необходимостта е доказана. и NSАВ. Нека покажем, че елементът NSсъщо ще бъде елемент от множеството C.
и NSАВ. Нека покажем, че елементът NSсъщо ще бъде елемент от множеството C. , означава NSC. Достатъчността е доказана.
, означава NSC. Достатъчността е доказана.
 ). По същия начин: NSА (или NSĀ). Тоест всеки елемент от комплекта
). По същия начин: NSА (или NSĀ). Тоест всеки елемент от комплекта  е също елемент от множеството Ā. И това може да е така, ако
е също елемент от множеството Ā. И това може да е така, ако  ... Q.E.D.
... Q.E.D.