Dikdörtgen bir koordinat sistemi ayarlama yöntemleri

Bilindiği gibi, düzlemdeki dikdörtgen koordinat sistemi üç şekilde ayarlanabilir: 1. yöntem, sistem merkezinin konumu ile sabitlenir - T., öküz ekseni yapılır ve pozitif yönü belirtilir, oy ekseni Öküz eksenine dik, sistem tipine göre (sağ veya sol), ılık ekseninin pozitif yönünü gösterir, koordinat ölçeği eksenler boyunca ayarlanır.

Koordinat eksenlerinin varlığında, herhangi bir noktadaki koordinatları belirlemek için, önce bu noktadan dikeyleri bu noktadan koordinat eksenlerine atlamalısınız ve ardından bunların uzunluğunu ölçmeniz gerekir; Dikin öküz eksenine dikin uzunluğu, Y koordinatına eşittir, eksen ekti koordinat x noktasına dikin uzunluğu (Şek. 1).

Xoy sistemine ek olarak, Koordinatların başlangıcını O "(xo" \u003d dx, yo "\u003d DY'ye aktararak Xoy sisteminden elde edilen X" O "Y" sistemini kullanabilirsiniz ve koordinat eksenlerinin bir açıyla saat yönünde döndürülmesi b.

Xoy ila X "O" Y "ye geçiş formüllerle yapılır:

Formüller ters geçiş için kullanılır:

• 2. Yöntem, karşılıklı olarak iki paralel çizgiler sistem sistemi gerçekleştirilir; Çizgiler arasındaki mesafeler aynıdır, bu hatların koordinat eksenlerine paralel olduğuna ve her satır karşılık gelen koordinatın değerini imzaladığına inanılmaktadır (koordinat ızgarası elde edilir).
• 3. yöntem, iki sabit noktalı koordinatların sayısal değerleri ile gösterilir.

İlk yöntem genellikle kabul edilir; Jeodezy'de, bu yöntem Gauss'un dikdörtgen koordinatlarının zonal sistemini ayarlar.

Topografik haritalar ve planlar üzerinde, dikdörtgen koordinatları Gauss sistemi ikinci sırada ayarlanmıştır.

Bölgede, dikdörtgen koordinat sistemi üçüncü yolla verilir; Bilinen koordineli birkaç jeodezik öğeyi bulabilir ve bu maddelere göre yeni noktaların konumunu belirleyebilir, herhangi bir ölçüm yapabilirsiniz.

Üç temel ölçüm

Uçakta açıları ve mesafeleri ölçebilirsiniz.

Açı üç nokta ile sabitlenir: bir nokta köşenin üstüdür ve diğer iki nokta, açının 1. ve 2. taraflarının yönlerini sabitler. En basit durumda, üçünün en az bir noktası koordinat yoktur, bu belirlenir; Genel durumda, bir nokta, iki nokta veya üçü de belirlenebilir.

Mesafe iki nokta ile sabitlenir ve genel olarak bir nokta veya her ikisi de belirlenebilir.

Bu bölüm, bir noktaların koordinatlarını belirlemek için açı veya mesafenin ölçülmesi yapıldığında en basit durumunu tartışır. Açıyı ölçerken, tanımlanmış nokta, açının üstünde veya taraflarından birinde bulunabilir, ardından bakış açımızdan, temel olarak adlandırılan üç farklı boyut vardır.

A'nın paragrafındaki açı, bilinen koordinatlar ile, Bab'ın bilinen bir yönlendirme köşesine olan yönü ile belirlenen noktaya yöneleyin (Şekil 2) yönü arasında bilinen koordinatlar ile ölçülür.

AP yönünün yönlü açısı, formül tarafından elde edilir.

P noktasının pozisyonu olarak adlandırılan düz bir Hat AP için, Xoy sistemine bir denklem yazabilirsiniz:

Bu denklem x ve y, P noktaları da dahil olmak üzere herhangi bir noktalı koordinatlar, ancak bu bir denklemin p noktasının iki koordinatını bulmak yeterli değildir.

S mesafe, bilinen Koordinatlar XA, YA, belirlenen P noktasına göre ölçülür. Geometrinin seyrine göre, P noktasının, A'nın etrafında harcanan ve aradığı ve aradığı bilinmektedir. P pozisyon satırı P (Şek. 3). Daire denklemi:

Bu denklem x ve y, p noktaları da dahil olmak üzere, pular dahil olmak üzere, ancak bu bir denklemin noktasının iki koordinatını bulmak için koordinatları yeterli değildir.

Tanımlanan P noktasındaki açı, bilinen koordinatlar olan iki noktaların yönleri arasında ölçülür; Bu ölçüm 8. bölümde görüntülenir.

P noktasının X ve Y noktaları, iki denklemin eklem çözeltisinden bulunabilir, bu nedenle iki üç boyutun herhangi bir kombinasyonunu alarak, jeodezik seriflerin koordinatlarını belirlemenin en basit yollarını elde ediyoruz: iki Tip (2.4) - doğrudan açısal gizli denklemler, iki denklem tipi (2.5) - lineer serif, tip (2.4) bir denklemi ve tip (2.5) polar gizlice bir denklemi, belirlenen noktada açıların iki ölçümü - ters açısal sektör.

Kalan ölçüm kombinasyonları kombine serifler denir.

Üç temel ölçümün her biri, farklı çizimlerde SERIF'leri çözmenize olanak tanıyan, P noktasının Sabit noktalar A ve B'nin grafiksel olarak konumunu belirlemenizi sağlayan koordinat sistemlerine göre bir değişmezdir.

Seriflerin çözümünün analitik yöntemi, belirlenen noktanın koordinatlarının hesaplanmasıdır. Gerçekleştirilen ölçümlere karşılık gelen iki denklem sisteminin çözeltisi veya bir üçgen çözeltisi, köşeleri iki kaynak noktası olan ve tanımlanmış nokta (kısalık için bu yöntem bir üçgen yöntemi olarak adlandırılır) yapılabilir.

Herhangi bir jeodezik yapıda, üç tür veri türünü tahsis etmek için gelenekseldir: başlangıç \u200b\u200bverileri (ilk öğelerin koordinatları, ilk yönlerin direktifi, vb.); Bu veriler genellikle şartlı olarak kusursuz, ölçülen unsurlar alınır; Her ölçülen elemanın genellikle ortalama ikinci dereceden bir ölçüm hatası, bilinmeyen (veya tanımlanmış) elemanları eşlik eder; Bu unsurlar, özel olarak geliştirilmiş bir algoritma bulmaya tabidir ve bu yapıların ölçüm hatalarına ve geometrisine bağlı olarak değerleri bir hata ile elde edilir.

Polar kardeş

Kaynak verilerindeki kaynak verileri, A'nın Paragrafı koordinatlarıdır ve AB yönünün (veya B) 'nin koordinatları) yönlerinin, ölçülen elemanların yatay açısıdır (MB açısını ölçme ortalama ikinci dereceden hatası) ve Uzaklığın (Ölçümünün Göreli Hatası MS / S \u003d 1 / T), bilinmeyen elemanlar - Koordinatlar X, Y Point P (Şekil 4).

Kaynak veri: xa, ya, bab

Ölçülen Öğeler: B, S

Bilinmeyen öğeler: x, y

Grafik çözümü. Ab yönünden, açının köşesini ertelemek ve doğrudan satır AQ'yu, daha sonra bir çevrenin etrafında, Çizim ölçeğinde (plan veya kart) içindeki yarıçapın bir arkını gerçekleştirin; Düz çizginin kesişme noktası ve ark istenen bir P'dir.

Analitik çözüm. Yönlü Açı B Line Ar:

Düz çizgi AP formülünün (4) denklemlerini ve A-Formül (5) paragrafının etrafındaki yarıçap dairesinin dairesini yazıyoruz:

P noktasının X ve Y koordinatlarını bulmak için, bu iki denklem sistem olarak bir araya getirilmelidir. Değerinin (Y - YA) ilk denklemden ikinciye kadar değiştiriyoruz ve parantez için (x - xa) 2:

(X - xa) 2 * (1 + tg2 b) \u003d S2.

İfade (1 + TG2B) 1 / COS2B'yi değiştirin ve:

(X - xa) 2 \u003d s2 * cos2b, burada x xa \u003d s * cosb.

Bu değeri ilk denklemde değiştirin (6) ve biz:

Y - ya \u003d s * sinb.

Koordinatların (X - XA) ve (Y - YA) farkı, artışları aramaya ve DX ve DY'yi belirtmek için gelenekseldir.

Böylece, kutupsal gizlice formüller tarafından açıkça çözülür:

koordinat üçgenleme trulaterasyonu

Uçakta doğrudan jeodezik görevi

Jeodezy'de iki standart görev vardır: düzlemde doğrudan bir jeodesk görevi ve uçağın ters jeodezik görevi vardır.

Doğrudan jeodezik görev, ilk öğenin X1, Y1 koordinatları, Direktif açısı B ve bu öğeleri bağlayan uzunluk s dizisini, ikinci öğenin X2, Y2 koordinatlarının hesaplanmasıdır. Doğrudan jeodezik görev, kutup Serif'in bir parçasıdır ve çözeltisi formülleri formülden (7) alınmıştır:

Uçakta Geodezik Görevi Ters

Ters jeodezik problem, X1, Y1 ve X2, Y2 ile bilinen koordinatlarla iki noktaları bağlayan, B açısının ve uzunluk satırının hesaplanmasıdır (Şekil 5).

Segment 1-2, hipotenuse üzerindeki koordinat eksenlerine paralel olan müşterilerle dikdörtgen bir üçgen olarak inşa ediyoruz. Hipotenüsün bu üçgesinde, Katenetler, 1 ve 2 (DX \u003d X2 - X1, Belge \u003d Y2 - Y1), ve keskin köşelerinden biri Rumba R hattından birinin eşit olduğu artışlara eşittir. 1-2.

D x 00 ve d y 00 ise, üçgeni ünlü formüllere göre çözeriz:

Bu model için, 1-2 çizginin yönü ikinci çeyrektedir, bu nedenle (22) temelinde (22) bulduk:

1-2 çizginin yöneticisi açısını bulmak için genel prosedür, iki işlemi içerir: Koordinat artışları açısından çeyrek sayının belirlenmesi D\u003e x ve dy, Hesaplama B İletişim formüllerine (22) göre Çeyrek numarasına göre hesaplama.

Hesaplamaların doğruluğunun kontrolü, eşitliğin uygulanmasıdır:

DX \u003d 0.0 ise, sonra s \u003d ідyі;

ve b \u003d 90o 00 "00" da\u003e 0,

b \u003d di ile 270o 00 "00"< 0.

D \u003d 0.0 ise, sonra s \u003d ідx_

ve b \u003d 0o 00 "00" dx\u003e 0,

b \u003d DX'te 180O 00 "00"< 0.

Ters problemi otomatik modda çözmek için (bilgisayar programlarında), açılı teğet içermeyen ve olası bölünmeyi sıfırdan ortadan kaldıran farklı bir algoritma kullanılır:

d \u003d\u003e 0O ise, sonra b \u003d a,

eğer dy.< 0o, то б = 360o - a.

Düz açısal kız kardeş

İlk olarak, B1 ve B2'nin açıları, bilinen koordinatlar olan, her biri bilinen bir yön açısıyla (Şekil 6) olan iki noktada ölçüldüğünde, doğrudan bir açısal sektörün genel durumunu göz önünde bulundurun.

Kaynak Veri: XA, YA, BAC,

Ölçülen öğeler: 1, B2'de

Bilinmeyen öğeler: x, y

BAC ve BBD belirtilmediyse, ters jeodezik sorunu ilk önce A ve C noktalarının ve ardından B ve D arasındaki noktaları arasında çözmek gerekir.

Grafik çözümü. AC yönünden, taşıyıcıyı kullanarak B1 açısını ertelemek ve doğrudan satırı AP'yi harcamak için; B2'nin açısını ertelemek için BD'nin yönünden ve doğrudan BP'nin doğrudan satırını harcamak; Bu doğrudan bunun kesişme noktası istenen nokta P'dir.

Analitik çözüm. Ortak bir serif durumuna karşılık gelen bir seçeneğin bir algoritması verelim:

yönlü Açılar AP ve BP Hatlarını Hesaplayın

doğrudan çizgilerin iki denklemini yazın

y - YA \u003d TGB1 * (x - XA), BP Y - YB \u003d TGB2 * (x - xb) (2.16) hattı için

İki denklemin sistemini çözün ve x ve y bilinmeyen koordinatları hesaplayın:

Doğrudan bir açısal sektörün özel bir durumu, B1 ve B2 açıları AB ve BA'nın yönlerinden ölçüldüğünde, B1 ve B2'nin açısı ile ölçüldüğünde ve B2 açısı solun (bir Her iki köşenin sektörü - sol) - şek. 7.

Üçgen yönteminin düz köşesinin çözeltisi, özel bir seks anahtarına karşılık gelir. Solüsyonun prosedürü bu olacaktır: A ve B'nin paragrafları arasındaki ters problemi çözmek ve Bab'ın dizin açısını ve AB çizgisinin uzunluğunu elde etmek için, Sefing açısı olarak adlandırılan P'nin üstündeki G'yi hesaplayın. ,

aPB üçgeni için sinüs teoremini kullanma:

partilerin AP (S1) ve BP (S2) uzunluklarını hesaplayın, B1 ve B2 dizini açılarını hesaplayın:

a noktasından P noktasından P ve kontrol için doğrudan bir görevi çözün - P. P. P. P.

X ve Y koordinatlarını doğrudan açısal bir sektörün belirli bir örneğinde hesaplamak için Jung'un formüllerini kullanabilirsiniz:

Genel durumdan, doğrudan köşe serf özel bir duruma geçmek zor değildir; Bunu yapmak için, önce, A ve B'nin paragrafları arasındaki ters jeodezik problemi çözmeniz ve AB çizgisinin Babının Müdürlüğü açısını elde etmeniz ve ardından APB üçgenindeki açıları A ve B'deki açıları hesaplar.

BAP \u003d BAB - (BAC + B1) ve ABP \u003d (BBD + B2) - BBA.

Makine hesabı için, doğrudan köşe serflerini çeşitli nedenlerle çözmenin tüm yolları rahatsız edicidir. Bir bilgisayarda bir serif vesayı çözmek için olası algoritmalardan biri, aşağıdaki işlemleri sağlar: B1 ve B2 dizin açılarının hesaplanması, yerel koordinat sisteminin tanıtılması x "O" y " A, "x" eksen, A ve B noktalarının koordinatlarının yeniden hesaplanması ve Xoy sisteminden Xoy sisteminden B1 ve B2 yönlendirme açılarının XOY sisteminden yeniden hesaplanması (Şekil 8):

X "a \u003d 0, y" a \u003d 0,

(24), AP ve BP çizgilerinin denklemlerini X "O" Y "sisteminde kaydetme:

ve bu denklemlerin ortak çözümü:

x "ve Y" 'nun Koordinatlarının Xoy sisteminde X "O" Y "sisteminden çevirisi:

CTGB2 "\u003d - CTGG ve G'nin tohum açısı her zaman 0O'dan büyük, daha sonra çözelti (27) her zaman var.

Doğrusal dikiş

A cinsinden bilinen koordinatlar XA, YA, S1'in belirtilen P noktasına kadar ölçüldüğü ve Bilinen Koordinatlar XB'li PARAGRAP'DAN, YB, S2'nin P noktasına kadar olan mesafeyi ölçtü.

Grafik çözümü. A'nın bir daire etrafında bir daire (çizim ölçeğinde) ve B'nin etrafında ve B - Yarıçapı S2 ile çevresine çevresinde gerçekleştiriyoruz; Dairelerin geçiş noktası istenen nokta; Görev, iki çember iki çember iki noktada kesilir (Şekil 9).

Orijinal Veriler: XA, YA, XB, YB,

Ölçülen elemanlar: S1, S2,

Bilinmeyen öğeler: X, Y.

Analitik çözüm. İki Analitik Çözüm Algoritması, bir manuel hesap için (bir üçgen metoduna göre) ve bir makine hesabı için bir tane olarak düşünün.

Manuel hesap algoritması aşağıdaki işlemlerden oluşur:

a ve B noktaları arasındaki ters jeodezik problemin çözünürlüğü ve Bab'ın yöneticisi açısının ve B1 uzunluğunun Ab Line Ab'i edinmesi, B1 ve B2 açılarının ABP üçgeni'ndeki hesaplama, kosinüs teoremi tarafından:

sERF'nin köşesinin hesaplanması

aP ve BP taraflarının dizin açılarının hesaplanması:

aB çizgisinin sağına P noktası

p noktasının solundaki sola

a fıçıdan PARAGRAP'tan PARAGRAPI PARAGRAPINDAN DOĞUTMA ÇÖZÜMÜN VE PARAGRAPI PARAGRAPI

1 çözüm

2. çözüm

Her iki çözümün de sonuçları çakışmalıdır.

Doğrusal Serif algoritması aşağıdaki işlemlerden oluşur: A ve B noktaları arasındaki ters jeodezik problemin çözümü ve Bab'ın yöneticisi açısını ve Boğanın Ab Lays Ab, yerel koordinat sisteminin tanıtılması X "O" Y " A ve A ekseni O "x" nin başlangıcında, AB çizgisi boyunca yönlendirilir ve A ve B noktalarının koordinatlarını Xoy sisteminden X "O" Y "sistemine yeniden hesaplayın:

x "O" Y "sisteminde daire denklemlerinin kaydı:

ve bu denklemlerin eklem çözümü, ikinci denklemdeki dirsekleri açıklamayı ve ikinci denklemi ilkden çıkarmayı içeren:

İstenen nokta AB çizgisinin solundaysa, "-" işareti, sağda ise, "+" formül (39) 'da alınır.

Koordinatların yeniden hesaplanması X "ve y" noktaları, XOY sistemine formüllere göre xoy sisteminde x "O" Y sisteminden "olarak yeniden hesaplayın (2):

Ters açısal kız kardeşi

İlköğretim Ölçümler, tanımlanmış nokta p arasında bir açı ölçümü, bilinen koordinatlar XA, YA ve XB, YB (Şekil 10) ile yöneldi. Ancak, bu ölçüm teorik olarak oldukça karmaşık olarak ortaya çıkıyor, bu yüzden ayrı ayrı düşünün.

Geometrinin okul yılında üç noktadan A, B ve P ile bir daire uygulayacağız, daire üzerinde bir köşe ile bir açının, dayandığı yarım bir yay ile ölçüldüğü bilinmektedir. Aynı yayeye dayanan merkezi açı, tüm ark tarafından ölçülür, bu nedenle, 2V'a eşit olacaktır (Şekil 10).

A ve B eşyaları arasındaki mesafe bilinmektedir ve dikdörtgen bir FCB üçgeninden RADIUS R çevresi bulunabilir:

Daire denklemi:

nEREDE XC ve YC, dairenin merkezinin koordinatlarıdır. A ve B PARAGRAP'larından bir C noktasında (42) X ve Y - P noktalarının herhangi bir noktasının koordinatları, P noktaları dahil olmak üzere, ancak iki koordinat bulmak için doğrudan bir açısal veya lineer bir serif kararıyla hesaplanabilirler. P noktasının Böyle bir denklem yeterli değil.

Ters Açı Noktası, Koordinat noktalarının, B1 ve B2'nin iki köşesi boyunca, belirlenen p noktasında, Twarnes A, B, C ile üç nokta arasındaki üç nokta arasında ölçülen, (Şekil 11) ile ölçülen koordinat noktalarını belirleme yöntemidir.

Grafik çözümü. Marsh grafik çözümleri yöntemini ters köşeye veriyoruz. Şeffaf bir kağıda (izleme) bir tabakada, B1 ve B2'nin açılarını total vertex p ile inşa etmek gerekir; Daha sonra çizime bir çekiş empoze edin ve hareket ettirin, depo üzerindeki arabaların yönünün A, B, C noktalarından geçtiğini sağlamak; P noktasını çizim üzerine bir carting ile geçirin.

Kaynak verileri: XA, YA, XB,

Ölçülen elemanlar: B1, B2.

Bilinmeyen öğeler: X, Y.

Analitik çözüm. Ters açısal sektörün analitik bir çözümü, daha basit görevler, örneğin, 2 doğrudan açısal serif ve bir doğrusal veya 3 lineer serifs, vb. Üzerine ayrışmasını sağlar. 10'dan fazla analitik çözüm yöntemi bilinmektedir, ancak yalnızca bir tanesini tutarlı bir üç lineer serif.

P noktasının konumunun bilindiği ve iki çevreyi gerçekleştireceğini düşündüğümüzü varsayalım: A, B ve P noktalarından bir yarıçap r1 ve B, C ve P ile bir başka yarıçap R2 ile bir yarıçap R1 (Şekil 11). Bu çevrelerin yarıçapı, formül (41) ile elde edilecektir:

Dairelerin merkezlerinin koordinatları - puan ve O2, P noktasının koordinatları, P noktasının koordinatları, Lineer Serif formülleri ile belirlenebilir: O1 noktasından R1 mesafeden ve O2 noktasından R2 mesafesidir.

O1 merkezinin koordinatları, R1 mesafelerinden A ve B noktalarından doğrusal serif formüllerine göre bulunabilir ve iki çözümden B1 açısının değerine karşılık gelen bir şeye girmeniz gerekir: eğer B1<90o, то точка O1 находится справа от линии AB, если в1>90o, o zaman O1 nokta AB çizgisinin solundadır.

Merkezi O2'nin koordinatları, R2 mesafelerinden B ve C noktalarından lineer serif formülleri üzerindedir ve iki olasıdan bir çözelti aynı kuralla seçilir: Eğer B2<90o, то точка O2 находится справа от линии BC, если в2>90O, o zaman O2 noktası BC hattın solundadır.

Her iki daire bir olarak birleştirildiğinden, dört nokta A, B, C ve P'nin de aynı dairede olduğunda görevin hiçbir çözümü yoktur ve kesişme noktası yoktur.

Kombine SERF'ler

Çözünürlükteki yöntem olarak kabul edilen yöntemlerde, sonucu sağlayan ölçüm sayısı teorik olarak minimum (iki boyut) alınmıştır.

Uygulamada, bir noktadan x ve y koordinatlarını bir kural olarak bulmak için, iki, ancak üç veya daha fazla mesafe ve açılar ölçümü yapmayın ve bu ölçümler hem kaynak noktalarda hem de belirlenenlerde gerçekleştirilir; Bu tür serifler birleştirildi. Bu durumda, kontrolün ölçme olasılığı göründüğü ve ek olarak, problem sorununun doğruluğunun artması.

Göreve girilen her ölçüm, teorik olarak minimum miktarda fazlalık denir; Bir ek çözüm oluşturur. Aşırı ölçümler olmayan jeodezik serifler tek, ancak fazla ölçümlere sahip serifler - çoklu.

Aşırı ölçümlerin varlığında, bilinmeyenlerin hesaplanması ayarlanarak gerçekleştirilir. Birden fazla serifizasyonun sıkı eşitlenmesinin algoritmaları, bilgisayarda otomatik bir hesapla kullanılır; Manuel hesap için basitleştirilmiş ayar yöntemlerini kullanın.

Herhangi bir çoklu Serif (ölçümlerin N) ayarlanması için basitleştirilmiş yöntemi, bağımsız tek bölümler için olası tüm seçeneklerin oluşumunu ve çözeltisini sağlar (numarası N-1'dir) ve ardından Nokta Koordinatının ortalama değerlerinin hepsinden hesaplanması İzin verilen değerde farklıysa elde edilen sonuçlar.

Nokta pozisyon hatası

Tek boyutlu bir alanda (on line), nokta konumu, bir koordinat X'in değeri ile sabitlenir ve konum hatası MP noktası, bu koordinatın ortalama kare hata mx'e eşittir. Noktanın gerçek konumu, X değerinin her iki tarafında, orada (x - t * mx) - (x + t * mx) - orada olabilir; Uygulamada, T katsayısı genellikle 2.0 veya 2.50'ye eşit olarak belirtilir.

İki boyutlu bir alanda (yüzeyde), noktanın konumu iki koordinatın değerleri ile sabitlenir ve nokta pozisyonu hatası iki değer ile ayarlanmalıdır: bu yöndeki pozisyonun yönü ve hatası . Noktanın gerçek konumunun bulunduğu geometrik şekil, farklı bir forma sahip olabilir; Özel durumda, nokta pozisyonu hatası her yöne aynı olduğunda, yarıçapı daire r \u003d MP elde edilir.

Noktanın iki boyut için pozisyonu, iki pozisyon çizgisinin kesişilmesinde elde edilir. Ölçülen mesafenin konumu satırı için, yarıçapın yarıçapı, başlangıçta ilk paragrafta (Şekil 2.12A); Başlangıç \u200b\u200bnoktası A'daki tepedeki ölçülen açı için, orijinal AB çizgisine bir açıyla gerçekleştirilen düz bir çizgi (Şekil 2.12B).

Ölçüm hataları nedeniyle, "pozisyon grubu" kavramını girmeniz gerekir. Ortalama bir kuadratik hata ile ölçülen bir mesafe için MS, bir dairesel kayış (halka) 2 * MS genişliği, RADII (S - MS) ve (S + MS) ile iki daire arasında; Ölçülen MB hatasındaki bir açıyla, bir noktada bir köşeli dar bir üçgen ve 2 * MB'nin üstündeki bir açıdır. Konum hattı, konum şerit simetrisinin eksenidir (Şekil 12).

İncir. 12. Konum hattı ve "pozisyon grubu" nokta p: a) ölçülen mesafe için, b) ölçülen açı için.

"Ölçüm hatası vektörü" kavramını tanıtıyoruz ve V ile belirir. Ölçülen mesafe için VS vektörü AP hattı (doğrudan veya geri) boyunca yönlendirilir ve bir modül VS \u003d MS; Ölçülen açı için, VV vektörü, AP'ye dik olarak yönlendirilir (sola veya sağdan) ve bir HB modülü \u003d S * MB / C, S \u003d A * P.

P noktası P, iki konum çizgisinin kesişiminde olmak, iki pozisyon bantının kesişilmesinde oluşturulan 4 kare konumun merkezidir (Şekil 13).

İncir. 13. 4. "Arayan pozisyonu: a) lineer serif, b) düz bir köşe noktasında,

Bu temel 4 kare bir paralelken bir paralelken olarak görülebilir, çünkü içinde çevre kemerleri teğetsel bölümlerle değiştirilebilir ve açının farklılaşçları doğrudan, paralel pozisyon çizgilerinin segmentleridir. P noktasındaki mesafeler, punta punti noktasının konumundaki farkı farklı yönlerde gösteren 4-kare öğün sınırlarına kadar olan mesafeler.

Konum hatları, 4-kömür konumunun 4-kömür konumunu, R ve (180o - g) köşelerindeki açıları olan hataların paralelogramlarını aradığımız, burada g (180o - g) hata arasındaki açı Vektörler v1 ve v2. Paralelkenliklerin yükseklikleri, N1 ve H2 vektörlerinin modüllerine sayısal olarak eşit olduğundan, paralelogramların tarafı bilinen formüllerle elde edilir:

Ünlü taraflara göre, hataların paralel olarakgramı ve bunlar arasındaki köşe (180O - D) arasındaki köşe, her iki diyagonalının uzunluğu hesaplanabilir: kısa - D1 ve uzun - D2:

Böylece, altı yöndeki nokta pozisyon hatası (Şek. 14), basit formüllerle ifade edilir; Diğer tüm formüller için daha karmaşık olacaktır.

P NOKTASYONUNUN NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTASI NOKTALARININ HAZIRLANMASI (P *) R2), eşit deneyim pozisyonu konumuna eşittir P (4 * A * B * Sing),

uzun çapraz yönde çakışan "en zayıf yönde" konumunda bir pozisyon hatası olarak:

uzun ve kısa çapraz köşegenlerden ortalama ikinci dereceden hataların paralel olarakgramı:

Uygulamada, üçüncü seçenek daha sık kullanılır, burada herhangi bir tek noktanın doğruluğunu değerlendirmek için formüller kolayca elde edilir:

kutup cinsiyeti (Şekil 4):

düz açısal dikişleme (Şekil 6, 7):

doğrusal serunel (Şekil 9):

ters açısal tohum (Şek. 11).

Bu sektörde, Point Hatası'nın sağ kısmı Formula P'nin üç terim içermesi gerekir:

lineer Serif Point O1'in kaynak noktalarından A ve B (MO1), Lineer Serif Point O2'nin kaynak noktalarından ve C ve C (MO2) hatası, Lineer Serif Point P'nin Hatası O1 ve O2 noktalarından hata. (MP),

G'nin tohum açısı, BC ve BA çizgilerinin nispi konumuna ve B1 ve B2 açılarına bağlıdır; Şekiller için. 11 Bu açı, formül tarafından hesaplanır:

Pek çok uygulama için, P noktasının gerçek pozisyonunun, P noktasındaki MP'lik yarıçapının yarıçapı dairesinin içinde olduğu varsayılmak yeterlidir. Sıkı teoride, kabul edilen kriterin radyal bir hata olarak adlandırılır. Ek olarak, bu teoride "elips hataları" (2. sıranın eğrisi), "ellips" (4. sıra eğrisi) ve diğerleri gibi bu teoride daha karmaşık kriterler de kullanılır.

N\u003e 2 (çoklu serif) ölçümlerin miktarı ile, P noktası, eşitlenmiş ölçüm değerlerine karşılık gelen N konum satırlarının kesişmesinde elde edilir; Konum bantları, kesişen, form 2 * n-kare. En büyük pozisyon hatası P Point, P noktasından bu çokgenin tepesine uzak mesafeden belirlenecektir. Şekil 14-B'den, üçüncü ölçümün pozisyon hatasını azaltmadaki rolü, p açıkça anlaşılır; Bu arada, bu şekilde ikinci boyut pratik olarak nokta pozisyon hatasının değerini etkilemez.

Dikdörtgen Koordinat Sistemi

Puan koordinatları kavramını belirlemek için, koordinatlarını belirleyeceğimiz koordinat sistemini tanıtmamız gerekiyor. Farklı koordinat sistemlerinde aynı nokta farklı koordinatlara sahip olabilir. Burada uzayda dikdörtgen bir koordinat sistemi düşüneceğiz.

AŞAĞIDAKİ BİR NOKTASI ALINDA ALIN VEYA $ (0.0.0) $ 'lık koordinatları tanıtıyoruz. Koordinat sisteminin başlangıcını diyoruz. Şekil l'de olduğu gibi, bu eksenler sırasıyla, bu eksenler olarak sırasıyla, üç karşılıklı dik eksen $ OX $, $ OY ve $ OZ $ OX, $ OY ve $ OZ $ olarak yürüteceğiz. Bu eksenler sırasıyla apscissa eksenleri, ordular ve başvuran olarak adlandırılır. Sadece eksenlerdeki ölçeği tanıtmak için kalır (tek segment) - uzaydaki dikdörtgen koordinat sistemi hazırdır (Şekil 1)

Şekil 1. Uzayda dikdörtgen koordinat sistemi. Author24 - Öğrenci İnternet Değişimi

Noktanın koordinatları

Şimdi herhangi bir noktada böyle bir koordinat sisteminde nasıl belirleneceğini analiz edeceğiz. Keyersiz bir noktaya değin $ m $ 'a alın (Şek. 2).

Koordinat eksenlerine dikdörtgen bir paralel olarak inşa ediyoruz, böylece $ O $ ve $ M $ karşıt zirvelerinin puanları (Şek. 3).

Şekil 3. Dikdörtgen bir paralelefed. Author24 - Öğrenci İnternet Değişimi

Sonra $ M $ Point, $ (x, y, z) $ koordinatları olacaktır, burada $ x $ sayısal eksenden bir değerdir $ Ox $, $ y $ - sayısal eksendeki değeri $ Oy $ ve $ Z $ $ oz $ sayısal eksen.

Örnek 1.

Aşağıdaki görevin bir çözüm bulmak gerekir: Şekil 4'te gösterilen paralellemenin köşelerinin koordinatlarını yazın.

Karar.

Point $ o $ koordinatların başlangıcı, bu nedenle, $ o \u003d (0,0,0) $.

$ Q $, $ n $ ve $ r $, $ Ox $, $ oz $ ve $ Oy $, sonra, sonra

$ Q \u003d (2,0,0) $, $ n \u003d (0,0,1.5) $, $ r \u003d (0,2.5.0) $

$ S $, $ l $ ve $ m $ 'daki, $ OXZ $, $ OXY $ VE $ OYZ $, sonra, sonra

$ S \u003d (2,0,1.5) $, $ l \u003d (2,2,5,0) $, $ r \u003d (0,2.5,1.5) $

Point $ P $ Koordinatlar $ p \u003d (2,2.5,5.5) $

Vektörün koordinatları iki noktada ve formül

Bir Vector'ı iki noktanın koordinatları ile nasıl bulacağınızı öğrenmek için, bizim tarafımızdan tanıtılan koordinat sistemini göz önünde bulundurmak gerekir. $ O $ no'lu $ 'dan $ Ox $ eksen yönünde, $ \\ Rehmentline (i) $ vektörünü, $ \\ OY $ eksen yönünde ertelemiz - tekli vektör $ \\ genel hat (J) $, ve birim vektör $ \\ aşırı çizgili (K) $ $ $ oz $ eksenini yönlendirmeniz gerekir.

Vektör koordinatları kavramını tanıtmak için, aşağıdaki teoremi tanıtıyoruz (burada kanıtını göz önünde bulundurmayacağız).

Teorem 1.

Uzayda keyfi bir vektör, aynı düzlemde yatan herhangi bir vektörde ayrıştırılabilir ve bu ayrışmadaki katsayılar tekrarlarca tanımlanacaktır.

Matematiksel olarak, şöyle görünüyor:

$ \\ Aşırı satır çizgisi (Δ) \u003d M \\ Tepeli (α) + n \\ REverLine (β) + l \\ REverline (γ) $

$ \\ Aşırı satır çizgisi (I) vektörleri $ \\ REVERLINE (J) $ ve $ \\ REVERLINE (K) $, dikdörtgen koordinat sisteminin koordinat eksenleri üzerine inşa edildiğinden, açıkça aynı uçağa ait olmayacak. Bu koordinat sisteminde, Theorem 1 tarafından bu koordinat sisteminde $ \\ REverline (Δ) $ anlamına gelir, aşağıdaki türü alabilir.

$ \\ REverLine (Δ) \u003d M \\ Tepeli (i) + N \\ Rehecline (J) + L \\ Rehecline (K) $ (1)

nerede $ n, m, l∈r.

Tanım 1.

Üç vektör $ \\ aşırı satır çizgisi (I) $, $ \\ REverline (J) $ ve $ \\ REverline (K) $ Koordinat vektörleri tarafından belirtilecektir.

Tanım 2.

$ \\ Respalet (i) $, $ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ forline (j) $ ve $ \\ \\ aşırı satır çizgisi (k) $ 'a ayrıştırma (1) önündeki katsayılar, bu vektörün tarafımızca belirtilen koordinat sisteminde koordinatları olarak adlandırılacak.

$ \\ overline (δ) \u003d (m, n, l) $

Vektörler üzerinde doğrusal işlemler

Teorem 2.

Tutar Teoremi: Herhangi bir sayıdaki vektörün toplamının koordinatları, ilgili koordinatlarının toplamı ile belirlenir.

Kanıt.

Bu teoremi 2 vektör için kanıtlayacağız. 3 ve daha fazla vektör için, kanıt benzer şekilde inşa edilmiştir. $ \\ Rehecline (α) \u003d (α_1, α_2, α_3) $, $ \\ repertline (β) \u003d (β_1, β_2, β_3) $ olsun.

Bu vektör aşağıdaki gibi yazılabilir.

$ \\ \\ respleline (α) \u003d α_1 \\ \\ `üst satır çizgisi (i) + α_2 \\ Rehecline (j) + α_3 \\ α_2 \\ $, $ \\ \\ α_3 \\ α α (β) \u003d β_1 \\ Rehecline (i) + β_2 \\ Overline (J) + β_3 \\ REVERLINE (K) $

Koordinatlardoğru ve doğrusal değerler (sayılar), noktanın herhangi bir yüzeyindeki veya uzaydaki konumunu belirler.

Topografya, dünyanın yüzeylerinin konumunu hem yerdeki doğrudan ölçüm sonuçları hem de kartların yardımı ile kolayca ve açıkça belirlemenizi sağlayan bu koordinat sistemlerini kullanır. Bu tür sistemler arasında coğrafi, düz dikdörtgen, kutup ve bipolar koordinatlar bulunur.

Coğrafi Koordinatlar (Şek. 1) - Açısal değerler: Latitude (J) ve boylam (L), Koordinatların kökenine göre nesnenin yüzeyindeki konumunu belirleme - Başlangıç \u200b\u200b(Greenwich) Meridyen'in ekvator ile kesişme noktaları . Haritada, coğrafi ızgara harita çerçevesinin her tarafındaki ölçekle gösterilir. Çerçevenin batı ve doğu tarafı meridyenler ve kuzey ve güney - paraleldir. Kart sayfasının köşelerinde, çerçevenin çerçevesinin kesişme noktalarının coğrafi koordinatları.

İncir. 1. Dünya yüzeyinde coğrafi koordinat sistemi

Coğrafi koordinatlar sisteminde, yer yüzeyinin herhangi bir noktasının koordinat başlangıcına göre konumu, açısal ölçülerde belirlenir. ABD'nin başlangıcında ve diğer birçok eyalette, ilk (Greenwich) Meridyen'in ekvatorla kesişme noktasını benimsemiştir. Böylece gezegenimizin tamamı için birleşmiş olan coğrafi koordinat sistemi, birbirinden önemli mesafelerde bulunan nesnelerin karşılıklı konumunu belirlemek için problem çözmek için uygundur. Bu nedenle, askeri bir durumda, bu sistem temel olarak balistik füzeler, havacılık vb. Gibi uzun menzilli savaşın kullanımı ile ilgili yerleşim yerleri yapmak için kullanılır.

Düz Dikdörtgen Koordinatlar(Şek. 2) - Nesnenin, alınan kökene göre konumunu belirleyen doğrusal değerler - karşılıklı olarak dik doğrudan (Koordinat eksenleri x ve y) kesişimi.

Topografyada, her 6 derecelik bir bölge kendi dikdörtgen koordinat sistemine sahiptir. X Eksen - Eksenel Meridyen Bölgesi, Axis Y - Ekvator ve Eksenel Meridyenin Kavşak Noktası Ekvator - koordinatların başlangıcı.

İncir. 2. Haritalarda düz dikdörtgen koordinatlar sistemi

Düz dikdörtgen koordinatların sistemi zonaldır; Dünyanın yüzeyinin Gauss projeksiyonunda görüntüsüne bölündüğü ve dünyanın yüzey noktaları görüntülerinin düzlemdeki konumlarının konumunu belirtmek için tasarlanmış olan altı genetik bölge için kurulur. Bu projeksiyonda.

Bölgedeki koordinatların başlangıcı, bölgenin diğer tüm noktalarının doğrusal olarak belirlendiği ekvator ile eksitli meridyenin kesişme noktasıdır. Bölge koordinatlarının kökeni ve koordinat eksenleri, yeryüzünün yüzeyinde kesinlikle tanımlanmış bir pozisyonda bulunur. Bu nedenle, her bir bölgenin düz dikdörtgen koordinatları sistemi, diğer tüm bölgelerin hem koordinat sistemleri hem de coğrafi koordinat sistemi ile ilişkilidir.

Noktaların konumunu belirlemek için doğrusal değerlerin kullanılması, hem yerde hem de haritada çalışırken hesaplamaları yapmak için çok uygun bir düz dikdörtgen koordinat sistemini çok kullanıyor. Bu nedenle, birliklerde bu sistem en geniş uygulamayı bulur. Dikdörtgen koordinatlar, arazinin noktaları, mücadele emirleri ve hedeflerinin konumunu gösterir, aynı koordinat bölgesi içindeki nesnelerin karşılıklı konumunu veya iki bölgenin bitişik bölümlerini belirler.

Polar ve Bipolar Koordinat Sistemleri yerel sistemlerdir. Askeri uygulamada, bölgenin nispeten küçük bölgelerinde, örneğin, yer işaretlerinin ve hedeflerin hedeflenmesi, yer işaretlerinin ve hedeflerinin yeri, yerellik şemalarının hazırlanması, vb. Hedefleme, bölgeye göre, bir noktanın pozisyonunu belirlemek için kullanılırlar. Dikdörtgen ve coğrafi koordinat sistemleri ile.

2. Coğrafi koordinatların belirlenmesi ve bilinen koordinatlardaki nesnelerin uygulanması

Haritadaki noktanın coğrafi koordinatları, en yakın paralelliklerden ve Meridyen, enlem ve boylamdan bilinir.

Topografik haritanın çerçevesi, her birinde 10 saniye boyunca bölünme noktalarıyla ayrılmış bir dakika boyunca kırılır. Çerçevenin yan taraflarında, enlemleri ve kuzey ve güney boylamında.

İncir. 3. Haritadaki noktanın coğrafi koordinatlarının belirlenmesi (Nokta A) ve coğrafi koordinatlar tarafından bir nokta uygulayarak (NOT B)

Kartın dakikasını kullanarak, şunları yapabilirsiniz:

1 . Haritadaki herhangi bir noktadaki coğrafi koordinatları belirleyin.

Örneğin, a noktalarının koordinatları (Şekil 3). Bunu yapmak için, A noktasından Güney Harita çerçevesinden en kısa mesafeyi ölçmeniz gerekir, ardından ölçülü batı çerçevesine uygulayın ve ölçülen segmentteki dakika ve saniye sayısını belirlemeniz, ortaya çıkan (ölçülen) dakikaları katlayın ve Çerçevenin güneybatı köşesinin genişliği ile saniyeler (0 "27") - 54 ° 30.

Enlem Haritadaki noktalar aşağıdakilere eşit olacaktır: 54 ° 30 "+0" 27 "\u003d 54 ° 30" 27 ".

Boylam Benzer şekilde belirlenir.

A noktasından Batı Kart çerçevesinden en kısa mesafe, bir sirkülatöre sahip bir sirkülatör kullanılarak ölçülür, güney çerçeveye dairesel bir ölçer uygulanır, ölçülen segmentte dakikalar ve saniye sayısını belirler (2 "35") Güney-batı köşe çerçevelerinin boylamıyla (ölçülen) değeri - 45 ° 00 ".

Boylam Haritadaki noktalar aşağıdakilere eşit olacaktır: 45 ° 00 "+2" 35 "\u003d 45 ° 02" 35 "

2. Belirtilen coğrafi koordinatlara göre karttaki herhangi bir noktayı uygulayın.

Örneğin, enlemin B noktası: 54 ° 31 "08", 45 ° 01 "41" boylam.

Boylamda bir nokta noktası uygulamak için, bu nokta boyunca gerçek meridyeni, kuzey ve güney çerçevesi boyunca aynı sayıda dakikanın bağlanması için gerçekleştirilmesi gerekir; Enlemde bir noktaya bir nokta uygulamak için, bu nokta boyunca paralel olarak, bunun için aynı sayıda dakikayı Batı ve Doğu çerçevesine bağlamak olması gerekir. İki düz çizginin kesişimi, B noktasının konumunu belirleyecektir.

3. Topografik haritalar ve sayısallaştırılması üzerine dikdörtgen koordinat ızgarası. Koordinat bölgelerinin ekleminde ek örgü

Haritadaki koordinat ızgarası, bölgenin koordinat eksenlerine paralel çizgilerle oluşan bir kare ızgaradır. Mesh hatları, bir tamsayı kilometre sayısından gerçekleştirilir. Bu nedenle, koordinat ızgarası da kilometre ızgara ve hatları kilometresi olarak da adlandırılır.

Haritada 1: 25000 çizgili koordinat ızgarasını oluşturan 4 cm, yani yerdeki 1 km, yani, 2 cm'den 1: 50000-1: 200000'den sonra (1,2 ve 4 km) kartlar üzerinde gerçekleştirildi. sırasıyla). 1: 500000 kartta, sadece 2 cm (zeminde 10 km) sonra her bir sayfanın iç çerçevesindeki koordinat ızgara çizgilerinin çıkışları uygulanır. Gerekirse, bu çıkışlarda, koordinat çizgileri karta uygulanabilir.

Topografik haritalarda, abscissa'nın değerleri ve koordinat çizgilerinin bulunduğu (şek. 2), kartın her bir sayfasındaki tabaka iç çerçevesinin ve dokuz yerdeki çizgilerin çıkışlarını işaretler. Kilometre cinsinden apsis ve ordaların komple değerleri, köşelere yakın koordinat satırları haritasının köşelerinin yakınında ve koordinat çizgilerinin geçmesinin kuzeybatı açısına yakın bir şekilde imzalanır. Kalan koordinat hatları, daha kısa iki hane (onlarca kilometre birimleri) ile imzalanır. Koordinat ızgarasının yatay çizgilerinin yakınındaki imzalar, Kilometre cinsinden tahrip ekseninin mesafelerine karşılık gelir.

Dikey çizgilerin yakınındaki imzalar bölge numarasını (bir veya iki basamakta) ve kilometre cinsinden (her zaman üç hane) mesafeden, koordinatların başlangıcından (her zaman üç hane) mesafesini, 500 km'lik bir eksenel Meridian bölgesinin batısına aktarılmıştır. Örneğin, imza 6740 anlamına gelir: 6 - Bölge numarası, 740, koordinatların koşullu kökeninden kilometre cinsinden mesafedir.

Dış çerçevede, koordinat hatlarının çıkışları verilir ( ek ızgara) İlgili bölge koordinat sistemleri.

4. Noktaların dikdörtgen koordinatlarının belirlenmesi. Kart noktalarında koordinatlarına göre başvuru

Bir dolaşım (cetvel) kullanarak koordinat kılavuzuyla şunları yapabilirsiniz:

1. Haritadaki dikdörtgen nokta koordinatlarını belirleyin.

Örneğin, noktaları (Şekil 2).

Bunu yapmak için gereklidir:

• x - NOKTA, I.E. 6657 Km'taki karenin alt kilometresini dijitalleştirin.
• aşağı Kilometre kare karesinden dik mesafeyi, haritanın doğrusal ölçeğini olan noktaya kadar ölçün, bu segmentin değerini metre cinsinden belirlemek;
• Ölçülen 575 m'lik ölçülen değeri, karenin alt kilometrik hattının dijitalleştirme değeri ile katlayın: x \u003d 6657000 + 575 \u003d 6657575 m.

PRIDININE Y'nin tanımı benzer şekilde üretin:

• y'nin değerini kaydet - karenin sol dikey çizgisini dijitalleştirin, yani.7363;
• bu satırdan dik mesafeyi B, T. E.335 m;
• Ölçülen mesafeyi, meydanın sol dikey çizgisinin Y'nin dijitalleştirme değerine ekleyin: Y \u003d 7363000 + 335 \u003d 7363335 m.

2. Hedefi belirtilen koordinatlara uygulayın.

Örneğin, Koordinatlardaki R noktası: X \u003d 6658725 Y \u003d 7362360.

Bunu yapmak için gereklidir:

• r noktasının tüm kilometrelerinin değeri olduğu bir kareyi bulun, yani 5862;
• segmentin karesinin sol alt köşesinden harita ölçeğinde ertelemek için, hedefin absikinin eşit farkı ve karenin alt tarafı - 725 m;
• elde edilen noktadan, segmenti ertelemek için sağa dik olan noktadan, koordinat hedefinin eşit farkı ve meydanın sol tarafı, yani 360 m.

İncir. 2. Haritadaki noktanın dikdörtgen koordinatlarının belirlenmesi (B noktası) ve dikdörtgen koordinatlar üzerinde bir nokta uygulayın (nokta D)

5. Çeşitli ölçekler haritalarında koordinatların belirlenmesinin doğruluğu

Kartlardaki coğrafi koordinatların belirlenmesinin doğruluğu 1: \u200b\u200b25000-1: 200000, sırasıyla yaklaşık 2 ve 10 "" dir.

Noktaların dikdörtgen koordinatları haritasında belirlenmenin doğruluğu, yalnızca ölçeğiyle değil, aynı zamanda bir haritayı çekerken veya farklı noktalar ve arazinin nesnelerini uygulayarak hataların değerleri de izin verilir.

En doğru olanı (0.2 mm'lik bir hata ile), karta jeodezik maddeler uygulanır. Arazi ve görülebilen en keskin olarak seçkinler (bireysel çan kulesi, fabrika boruları, kule tipi inşaat) olan (bireysel çan kulesi, fabrika boruları). Bu nedenle, bu noktaların koordinatları, karta uygulandıkları aynı doğrulukla, yani, 1: 25000 ölçeği ile - 5-7 m, ölçek ölçeği için 1: 25000 - 5-7 m haritası için de belirlenebilir. : 50000 - Doğruluk ile - 10-15 m, Harita Ölçeği 1: 100000 - Hassasiyetle - 20-30 m.

Konturların kalan kriterleri ve noktaları, karta uygulanır ve bu nedenle ve dolayısıyla 0,5 mm'ye kadar olan bir hatayla ve arazi ile ilgili kontürlerle ilgili noktaları (örneğin, bataklık devresi) ile ilgilidir. ), 1 mm'ye kadar bir hatayla.

6. Polar ve bipolar koordinat sistemlerinde nesnelerin (noktaları) konumunun belirlenmesi, yöndeki nesnelerin haritasına, iki köşeye veya iki mesafede

Sistem düz polar koordinatları (Şek. 3, A) Koordinatların kökeninin etrafındaki bir noktadan oluşur veya kutuplar, ve ilk yön veya çağrılan kutup ekseni.

İncir. 3. A - Polar Koordinatlar; B - Bipolar Koordinatlar

Yerindeki veya bu sistemdeki haritadaki M'nin konumu, iki koordinatla belirlenir: Polar Eksenden gelen saat yönünde ok boyunca ölçülen konumun açısı, belirlenen noktaya ( 0 ila 360 °) ve ABS \u003d d.

Direğin problemine bağlı olarak, gözlem maddesi, ateşleme pozisyonu, başlangıç \u200b\u200bnoktası, vb., Ve polar ekseni için - coğrafi (gerçek) meridyen, manyetik meridyen (pusula manyetik ok yönü) veya herhangi bir dönüm noktasında yön.

Bu koordinatlar, A ve B noktalarından istenen noktaya kadar talimatları belirleyen pozisyonun iki açısına veya D1 \u003d S ve D2 \u003d VM mesafesini belirleyebilir. Şekil l'de gösterildiği gibi, aynı zamanda pozisyonun köşeleri. 1, B, A ve B noktalarında veya bazında (yani, A \u003d Siz ve A açısı B \u003d AVM) veya A ve B noktalarından geçen diğer yönlerden ölçülen ve ilk için alınan diğer yönlerden ölçülür. Örneğin, ikinci durumda, M, M, Magnetik meridyenlerin yönünden ölçülen, θ1 ve θ2 konumunun açısı ile belirlenir. Sistem düz Bipolar (Bipolar) Koordinatlar (Şekil 3, b) iki kutuplu A ve B ve AB'nin toplam ekseni, Serif'in temeli veya tabanı olarak adlandırılır. MAP (MAP (LOCACY) noktalarının A ve B'deki iki veriye göre M'nin herhangi bir noktasının konumu, harita üzerinde veya zemin üzerinde ölçülen koordinatlar tarafından belirlenir.

Bir haritada algılanan bir nesnenin uygulanması

Bu, nesnenin tespitinde en önemli anlardan biridir. Nesnenin (hedef) karta tam olarak nasıl uygulanacağı, koordinatlarının belirlenmesinin doğruluğu bağlıdır.

Bir nesneyi bulma (hedef), önce tespit edilen çeşitli özellikleri tam olarak belirlemelisiniz. Ardından, nesnenin gözlemini durdurmadan ve kendini tespit etmeden, karta bir nesne uygulayın. Haritada bir nesneyi uygulamak için birkaç yol vardır.

Eyemervan: Ünlü referans noktasının yanındaysa, nesne karta uygulanır.

Yön ve mesafe: Bunu yapmak için, haritayı yönlendirmeniz, üzerinde durmanızın noktasını bulun, harita yönünü algılanan nesneye asın ve çizgiyi duran noktasından okuyun, ardından mesafeyi belirleyin. Nesne, harita üzerinde bu mesafeyi ölçmek ve harita ölçeğinde görülmeye değer.

İncir. 4. Karttaki hedefin uygulanması Direct serif iki noktadan.

Böylece görevi çözmek için grafiksel olarak imkansız ise (düşmana, kötü görünürlük vb. İle müdahale eder), daha sonra Azimut'u nesneye doğru bir şekilde ölçmeniz, ardından dizin açısına çevirmeniz ve haritayı noktadan okunmanız gerekir. üzerinde dururken, nesneye olan mesafeyi ertelemek için.

Bir dizin açısı elde etmek için, bu kartın manyetik azimut (yön değişikliği) manyetik düşüşünü eklemek gerekir.

Direkt gizlice. Bu yöntem, bir karttaki bir nesnenin 2 ila 3 noktalı bir nesneden kaynaklanır, bunlardan izleyebileceğiniz. Bunu yapmak için, seçilen her noktadan nesneye yönlendirilmiş bir harita yönünde izlenir, daha sonra doğrudan çizgilerin kesişimi nesnenin yerini belirler.

7. Haritada hedef atama yöntemleri: Grafik koordinatlarda, düz dikdörtgen koordinatlarda (tam ve kısaltılmış), kilometre ızgarasının karelerinde (bir bütün kareye kadar, 1/4'e kadar, 1/9 kareye kadar), referans noktası, şartlı çizgiden, azimut ve bipolar koordinat sistemindeki hedefler aralığından

Hedefleri, yönergeleri ve yerdeki diğer nesneleri hızlı ve doğru bir şekilde gösterme yeteneği, savaşta ya da savaşta yer alan bölümleri ve yangını yönetmek için önemlidir.

En İyi Açıklama B. coğrafik koordinatlar Çok nadirdir ve yalnızca hedeflerin haritadaki belirtilen noktadan çıkarıldığı durumlarda, düzinelerce veya yüzlerce kilometrede ifade eden önemli bir mesafededir. Aynı zamanda, coğrafi koordinatlar, bu sınıfların 2 numaralı sorusunda açıklandığı gibi harita tarafından belirlenir.

Hedefin (nesnenin) konumu, örneğin, yükseklik 245.2 (40 ° 8 "40" s., 65 ° 31 "00" c. D.). Doğu (Batı), topografik çerçevenin kuzey (güney) tarafı, hedef pozisyonun enlemde ve boylamda işaretlemesinin dolaşımıyla uygulanır. Bu işaretlerden topografik kartın derinliğine kadar, kesişme noktalarına dik olarak indirilir (komutan kurallarını, standart kağıt sayfalarını uygulayın). Dikeylerin kesişme noktası ve haritadaki hedefin konumudur.

Yaklaşık hedef belirleme için dikdörtgen koordinatlar Nesnenin bulunduğu haritadaki örgü karesinin karesini belirtmek yeterlidir. Kare, her zaman Kavşağı Güney-Batı (sol alt) açısı tarafından oluşturulduğu kilometre çizgilerinin sayıları ile gösterilir. Kartın karesini belirlerken, kurallar takip edilir: ilk önce yatay çizgi (batı tarafında), yani "x" koordinatı ve ardından dikey çizgide iki rakam olarak imzalanan iki rakamı ararlar (güney) Sayfanın yüzü), yani "Y" koordinatı. Aynı zamanda, "x" ve "Y" konuşmuyor. Örneğin, tanklar düşmandır. Raporu radyo telefon numarasına iletirken, kare numarası telaffuz edilir: "Seksen sekiz sıfır iki."

Noktanın (nesnenin) konumu daha doğru olarak belirlenmesi halinde, ardından tam veya kısaltılmış koordinatları kullanın.

İle çalışmak tam koordinatlar. Örneğin, yol işaretçisinin koordinatlarını 8803 karesinde 1: 50.000 ölçek haritasında belirlemesi gerekir. İlk olarak, karenin alt yatay tarafındaki mesafeyi yol göstergesine (örneğin, yerdeki 600 m) belirler. Aynı şekilde, meydanın sol dikey tarafındaki mesafe ölçülür (örneğin, 500 m). Şimdi kilometre satırlarını sayarak, nesnenin toplam koordinatlarını belirliyoruz. Yatay çizgide 5988 (x) bir imzasına sahiptir, bu satırdan yol işaretçisine mesafe ekleyerek: x \u003d 5988600. Benzer şekilde, dikey çizgiyi de belirliyoruz ve 2403500 kazanıyoruz. Yol işaretçisinin toplam koordinatları aşağıdaki gibidir: x \u003d 5988600 m, y \u003d 2403500 m.

Kısaltılmış koordinatlar Buna göre, onlar eşit olacaktır: x \u003d 88600 m, y \u003d 03500 m.

Hedefin karadaki konumunu netleştirmek istiyorsanız, hedef belirlemeyi kilometrelik ızgaranın karesinin içindeki harf veya dijital yöntemle uygulayın.

Hedefleme için harfler Kilometre örgüsünün karesinin içinde, kare şartlı olarak 4 bölüme ayrılmıştır, her bölüm Rus alfabesinin büyük harf atanır.

İkinci yol - Dijital moda Bir kilometre kare içindeki hedef tasarım (hedef atama salyangoz ). Bu yöntem, kilometre ızgarasının içindeki koşullu dijital karelerin bulunduğu yerde adını aldı. Meydanı 9 bölüme ayrılırken spiral üzerinde düzenlenirler.

Bu durumlarda hedefleme durumunda, kare hedef olarak adlandırılır ve hedefin içindeki hedefin konumunu belirten bir harf veya şekil ekleyin. Örneğin, 51.8 (5863-a) veya yüksek voltajlı destek (5762-2) (bkz. Şekil 2).

Hedef belirleme, tasarlamanın en basit ve ortak yoludur. Bu durumda, hedefleme yöntemi ilk olarak en yakın dönüm noktası olarak adlandırılır, ardından kıyaslama üzerindeki yön arasındaki açının değeri ve müzakerenin (dürbünlerle ölçülen) ve hedefe çıkarılması için hedef üzerindeki açının değeri metre. Örneğin: "Benchmark, ikinci, ayrı bir kırk, ayrı bir çalı - bir makineli tüfek."

Tutulma koşullu hattan Genellikle savaş makinelerinde hareket halinde uygulanır. Bu durumda, haritadaki yöntem eylem yönünde iki nokta seçilir ve hedef belirlemenin yapılacağı göreceli olarak onları düz çizgiye bağlayın. Bu çizgi harflerle, santimetre bölümlerine ayrılmıştır ve bunları sıfırdan uyuşturur. Bu inşaat, hem verici hem de hedef belirlemenin haritalarında yapılır.

Koşullu hattın hedef belirlemesi genellikle savaş araçlarında hareket halinde uygulanır. Bu durumda, haritadaki yöntem eylem yönünde seçilir. Bu çizgi harflerle, santimetre bölümlerine ayrılmıştır ve bunları sıfırdan uyuşturur.

İncir. 5. Koşullu hattan kameralar

Bu inşaat, hem verici hem de hedef belirlemenin haritalarında yapılır.

Hedefin geleneksel çizgiye göre konumu, iki koordinatla belirlenir: başlangıç \u200b\u200bnoktasından dikin tabanına, hedefin konumu noktasından koşullu çizgiye ve koşullu olarak dik segmentten düşürülür. Hedefe çizgi.

Takdir olduğunda, hattın koşullu adı, daha sonra birinci segmentte ve nihayet, nihayet (sol veya sağda) ve ikinci bölümün uzunluğunu içeren santimetre ve milimetre sayısını denir. Örneğin: "Doğrudan AC, beş, yedi; Sağ sıfır, altı - np ".

Koşullu çizginin hedef belirlenmesi, hedefin yönünü şartlı çizginin açısında ve hedefe olan mesafeyi belirleyerek verilebilir, örneğin: "Doğrudan AC, Haklar 3-40, bin iki yüz makineli tüfek."

Tutulma azimut'ta ve hedefe. Hedef üzerindeki azimut yönü, derecelerde bir pusula kullanılarak ve aralığı - bir sürveyans aygıtı veya gözlerdeki gözlerin yardımı ile belirlenir. Örneğin: "Azimut otuz beş, açmada altı yüz tank." Bu yöntem en sık yerlerde, az sayıda yer işaretleri olduğu yerde kullanılır.

8. Görevlerin Çözümü

Alanın alanlarının (nesnelerin) koordinatlarının belirlenmesi ve karttaki hedef atama, pratik olarak önceden hazırlanmış noktalardaki (uygun nesneler) eğitim kartlarında uygulanır.

Her bir öğrenilen coğrafi ve dikdörtgen koordinatların tanımlanması (bilinen koordinatlara göre nesneleri verir).

Kartta tanımlanmanın yolları uygulanır: düz dikdörtgen koordinatlarda (tam ve kısaltılmış), bir kilometre ızgarasının karelerinde (bir bütün kareye kadar, 1/4'e kadar, 1/9 kareye kadar), referans noktasından, azimut ve hedef aralıkta.

Bu yazıda, basit aritmetik için birçok geometri görevini azaltmanıza izin veren bir "kıyıstak çubuğu" tartışmasına başlayacağız. Bu "stick", özellikle mekansal figürlerin, bölümlerin vb. İmzalanmasında güvenilir bir şekilde hissettiğinizde yaşamınızı önemli ölçüde hafifletebilir. Tüm bunlar, belirli bir hayal gücü ve pratik becerileri gerektirir. Burada düşünmeye başlayacağımız yöntem, her türlü geometrik yapı ve akıl yürütmeden neredeyse tamamen özetlemenizi sağlar. Yöntem denir "Koordinat Yöntemi". Bu yazıda aşağıdaki soruları göz önünde bulunduracağız:

1. Koordinat uçağı
2. Uçaktaki puanlar ve vektörler
3. İki nokta boyunca bir vektör oluşturmak
4. Vektör uzunluğu (iki nokta arasındaki mesafe)
5. Kesimin ortasının koordinatları
6. Skaler ürün vektörleri
7. İki vektör arasındaki köşe

Bence koordinat yönteminin neden böyle olduğunu tahmin ettin mi? Doğru, geometrik nesnelerle değil, sayısal özellikleriyle (koordinatlar) çalıştığı gibi, böyle bir isim aldı. Ve dönüşümün kendisi geometriye cebire taşınmanıza izin veren, koordinat sistemini tanıtmaktır. Kaynak rakamı düz ise, koordinatlar iki boyutludur ve eğer formasyon rakamı ise, koordinatlar üç boyutludur. Bu yazıda sadece iki boyutlu bir davayı göz önünde bulunduracağız. Makalenin asıl amacı, koordinat yönteminin bazı temel tekniklerini kullanmanızı öğretmektir (bazen b bölümündeki planlarda sorunları çözmede bazen faydalıdır). Bu konudaki aşağıdaki iki bölüm, C2 görevlerinin sorunlarını çözme yöntemlerini (stereometri için görev) çözmek için aynı yöntemleri tartışmaya adanmıştır.

Koordinat yöntemini tartışmaya başlamak için neden mantıklı olacaktır? Muhtemelen, koordinat sistemi kavramı ile. İlk olarak karşılaştığını hatırlayın. Bana göre, örneğin bir doğrusal fonksiyonun varlığını öğrendiğinde, 7. sınıfta göründüğü gibi görünüyor. Sana hatırlatmama izin ver, puanla inşa ettin. Hatırlıyor musun? Keyfi bir numara seçtiniz, formülde ikame edilmiş ve bu şekilde hesapladınız. Örneğin, eğer, öyleyse, eğer, sonra vb., Sonunda ne aldınız? Ve koordinatlarla bir nokta aldım: ve. Daha sonra, "çapraz" (koordinat sistemi) boyandınız, üzerinde bir ölçek seçtiniz (kaç hücre tek bir segmentiniz olacaktır) ve bunun üzerine alınan noktaları, elde edilen noktaları, elde edilen çizgiyi ve bir fonksiyon grafiği.

Size biraz daha açıklanması gereken birkaç dakika var:

1. Sebepler için seçtiğiniz tek bir segment, böylece her şey güzel ve kompakt olarak resme sıkıştırma

2. Eksenin sağa sağa gitmesi kabul edilir ve eksen alt tarafa

3. Dik açılarda kesişirler ve kesişme noktasının, koordinatların başlangıcı olarak adlandırılır. Mektupla belirtilir.

4. Noktadaki koordinatların kaydedilmesinde, örneğin, soldaki parantez içinde eksen boyunca ve sağdaki eksen boyunca bir nokta koordinatı vardır. Özellikle, sadece noktanın olduğu anlamına gelir

5. Koordinat eksenine herhangi bir noktayı ayarlamak için, koordinatlarını belirlemek için gereklidir (2 sayı)

6. Eksen üzerinde yatan herhangi bir nokta için,

7. Eksen üzerinde yatan herhangi bir nokta için,

8. Eksen abscissa ekseni olarak adlandırılır.

9. Eksen koordinat ekseni olarak adlandırılır.

Şimdi bir sonraki adımı sizinle yapalım: İki nokta not ediyoruz. Bu iki noktayı bir segmentle bağlayın. Ve okunu nokta için bir segmenti geçirirmiş gibi ok koyun: yani, bizim segmentimizi yöneteceğiz!

Yönlendirilmiş segmentin nasıl adlandırıldığını unutmayın? Doğru, bir vektör denir!

Böylece, eğer bir nokta ile bir nokta bağlarsak, dahası, bir noktaya sahip olacağız ve biti B, B Sonra bir vektör alıyoruz. Bu binayı 8. sınıfta yaptınız mı, hatırladın mı?

Puan gibi vektörlerin iki sayıyla gösterilebileceği ortaya çıktı: Bu numaraların vektör koordinatları denir. Soru: Koordinatlarını bulmak için vektörün başlangıcını ve sonunun koordinatlarını bilmemiz yeterli olduğunu düşünüyor musunuz? Evet, evet! Ve çok basit yapılır:

Böylece, nokta vektörü başlangıç \u200b\u200bolduğundan ve son olduğundan, vektör aşağıdaki koordinatlara sahiptir:

Örneğin, eğer, vektörün koordinatları

Şimdi tam tersine yapalım, vektörün koordinatlarını bulacağız. Bunun için ne değişmeli? Evet, başlangıç \u200b\u200bve sonu değiştirmeniz gerekir: şimdi vektörün başlangıcı noktada olacak ve sonuncu noktada. Sonra:

Dikkatlice bak, vektörler arasındaki fark nedir ve? Onların tek farkı koordinatlardaki işaretlerdir. Tam tersi. Bu gerçek şu şekilde kaydetmek için kabul edilir:

Bazen, özellikle öngörülmemesi durumunda, hangi nokta vektörün başlangıcıdır ve bunlardan ne kadar bitti, vektörler iki büyük harfle gösterilir, ancak bir satır, örneğin:, vb.

Şimdi biraz pençe Ve aşağıdaki vektörlerin koordinatlarını bulun:

Kontrol:

Ve şimdi biraz daha karmaşık bir soruna karar vermek:

Bir yüzyılda, noktada ka-hurdaya sahip bir CO-OR-DI-ON-SİZE vardır. Nai-tohum abs ciss dop.

Aynısı oldukça nesirdir: Noktanın koordinatlarını bırakın. Sonra

Vektörün koordinatlarını belirlemek için bir sistemim. Sonra nokta koordinatları var. Abscissa ile ilgileniyoruz. Sonra

Cevap:

Vektörlerle başka ne yapabilirsin? Evet, neredeyse her şey sıradan sayılarla aynıdır (bölemezseniz, bir kısmı burada bir süre sonra tartışacağımız iki yolla çarpmak mümkündür)

1. Vektörler birbirleriyle katlanabilir
2. Vektörler birbirinden düşülebilir
3. Vektörler keyfi bir sıfır olmayan numaraya çarpılabilir (veya bölünür)
4. Vektörler birbirleriyle çarpılabilir

Bütün bu işlemler tamamen görsel geometrik bir gösterime sahiptir. Örneğin, ekleme ve çıkarma için bir üçgenin (veya paralel birogram) kuralı:

Vektör gerilmiş veya sıkıştırılmış veya çarpma veya bölünürken yönü değiştirilir:

Ancak, burada koordinatlarla neler olup bittiğinin sorusu ile ilgileneceğiz.

1. İki vektörün (çıkarılması) (çıkarma) eklenirken, (kesinti) dönüşümlü olarak koordinatlarını katlıyoruz. Yani:

2. Vektörün sayısının (bölünmesini) çarparken, tüm koordinatları bu numaraya çarpılır (bölünmüş):

Örneğin:

· CO-or-Di-Nat'ın göz kapağının toplamını nay-die.

İlk önce vektörlerin her birinin koordinatlarını bulalım. İkisi de aynı başlangıçta - menşein noktası. Farklı uçları var. Sonra. Şimdi vektörün koordinatlarını hesaplıyoruz, sonra elde edilen vektörün koordinatlarının toplamı eşittir.

Cevap:

Şimdi aşağıdaki görev:

· Vektörin koordinatlarının toplamını bulun

Kontrol:

Şimdi aşağıdaki görevi düşünelim: Koordinat düzleminde iki noktamız var. Aralarındaki Mesafe Nasıl Bulunur? Birinci nokta olsun, ikincisi. Aralarındaki mesafeyi belirtir. Netlik için aşağıdaki çizim yapalım:

Ne yaptım? Birincisi, önce, ilk, bağlı noktalar ve ayrıca çizgiyi, eksene paralel olarak bir noktadan geçirdi ve çizgiyi eksene paralel olarak geçirdi. Harika bir figür oluşturarak noktada geçtiler mi? Ne harika? Evet, neredeyse sadece dikdörtgen üçgeni biliyoruz. Pythagora teoremi - kesin. İstenilen segment, bu üçgenin hipoten kullanımıdır ve segmentler Kartets. Noktanın koordinatları nelerdir? Evet, resimlerde bulmak kolaydır: Segmentler eksenlere paralel olduğundan ve buna göre, uzunlukları bulmak kolaydır: Sigaraların uzunluğunu belirlerseniz, o zaman

Şimdi Pisagor teoremini kullanıyoruz. Katetlerin uzunluğunu biliyoruz, hipotenüs bulacağız:

Böylece, iki nokta arasındaki mesafe, koordinatlardan farklılıkların karelerinin toplamının köküdür. Veya - iki nokta arasındaki mesafe, bunları birbirine bağlayan segmentin uzunluğudur. Noktalar arasındaki mesafenin yöne bağlı olmadığını fark etmek kolaydır. Sonra:

Buradan üç çıktı yapıyoruz:

İki nokta arasındaki mesafenin hesaplanmasında biraz egzersiz yapalım:

Örneğin, eğer, o zaman mesafe arasında ve eşittir

Ya da farklı şekilde gidelim: vektörün koordinatlarını buluruz

Ve vektörün uzunluğunu bulun:

Gördüğünüz gibi, aynı şey!

Şimdi biraz pratik yapın:

Görev: Belirtilen noktalar arasındaki mesafeyi bulun:

Kontrol:

İşte aynı formülde başka bir iş çifti, ancak biraz farklı görünüyorlar:

1. göz kapağının uzunluğunun nay-di kvad-fare.

2. Eyelid-RA uzunluğunun Nay-di Kvad-Fare

Bence, kolayca onlarla başardın mı? Kontrol:

1. ve bu dikkat çekiyor) Biz zaten vektörlerin koordinatlarını bulduk ve daha önce:. Sonra vektör koordinatları var. Uzunluğunun karesi eşit olacaktır:

2. Vektör koordinatlarını bulun

Sonra uzunluğunun karesi eşittir

Hiçbir şey zor değil mi? Sıradan aritmetik, artık yok.

Aşağıdaki görevler açıkça sınıflandırılamıyor, daha genel bir duruma benziyorlar ve yeteneğe basit resimler çizerler.

1. NA-KLO-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON-ON NOKTA'NIN ASCISSA ekseni ile.

ve

Buraya nasıl geleceğiz? Sinüs açısını ve eksenini bulmak için gereklidir. Ve sinüs nasıl aranacağını nereden biliyoruz? Doğru, dikdörtgen bir üçgende. Peki ne yapmamız gerekiyor? Bu üçgeni inşa et!

Noktadaki koordinatlardan bu yana, daha sonra segment eşittir ve segment. Sinüs köşesi bulmamız gerekiyor. Sinüsün, hipotenüs için zıt catech'in tutumu olduğunu hatırlatacağım, sonra

Ne yapmalıyız? Hipotenüs bulmak. Bunu iki şekilde yapabilirsiniz: Pythagore teoremine göre (Katenetler bilinir!) Veya iki nokta arasındaki mesafe formülü (aslında ilk yolla aynı şey!). İkincisi gideceğim:

Cevap:

Bir sonraki görev size daha kolay görünecek. O noktanın koordinatlarında.

Görev 2. ABS ekseninde Oposchn kalem-pen-di-yalancı noktasından. NAI-DIDE ABS CIS-SU OS-NO-VIA-PEN-DI-KU-LA-RA.

Bir çizim yapalım:

Dikin tabanı, abscissa ekseninin (eksen) 'nin haçlarının nokta olduğu noktadır. Şekil, koordinatları olduğunu göstermektedir :. Abscissa ile ilgileniyoruz - yani "ons" bileşenidir. Eşittir.

Cevap: .

Görev 3. Önceki görevin şartları altında, noktadan koordinat eksenlerine olan mesafeyi bulun.

Noktadan eksenlere olan mesafenin ne olduğunu biliyorsanız, görev genellikle temeldir. Bilirsin? Umarım, ama yine de size hatırlatır:

Öyleyse, çizimimde, hemen yukarıda bulunan, zaten bir dikey olarak tasvir ettim? Eksen nedir? Eksene. Ve o zaman uzunluğunun uzunluğu nedir? Eşittir. Şimdi eksene dikim var ve uzunluğu buluyorum. Eşit olacak, değil mi? Sonra tutarı eşittir.

Cevap: .

Görev 4. Sorunlar 2 açısından, noktanın sırasını, abscissa eksenine göre simetrik nokta.

Sanırım sezgisel olarak simetrinin ne olduğunu nelerdir? Sahip olan çok sayıda nesne sahiptir: birçok bina, masa, uçaklar, birçok geometrik şekil: top, silindir, kare, eşkenar dörtgen vb. Kabaca konuşursak, simetri anlaşılabilir: Şekil, aynı yarının iki (veya daha fazla) oluşur. Böyle bir simetri eksenel denir. Eksen ne var? Bu, rakamın aynı yarıları "kesim" olarak göreceli olarak konuşabileceği, (bu resimde simetri ekseni düz) olabilir) aynı çizgidir.

Şimdi görevimize geri dönelim. Eksen hakkında simetrik bir nokta aradığımızı biliyoruz. Sonra bu eksen simetri eksenidir. Bu yüzden, böyle bir noktadan bahsetmemiz gerekir, böylece eksen segmentini iki eşit parçaya kesebilir. Böyle bir noktayı kutlamak için kendini dene. Ve şimdi kararımla karşılaştırın:

Aynısını yaptın mı? Tamam! Bulunan noktada sıradan ile ilgileniyoruz. Eşittir

Cevap:

Ve şimdi söyle bana, saniyeler, abscissa noktası ne olacak, simetrik nokta koordinat eksenine göre? Cevabın nedir? Doğru cevap: .

Genel durumda, kural böyle yazılabilir:

Abscissa eksenine göre simetrik nokta, koordinatlara sahiptir:

Noktaya, koordinat eksenine göre simetrik nokta, koordinatlara sahiptir:

Peki, şimdi oldukça korkunç bir görev: Koordinatların başlangıcına göre, simetrik nokta, simetrik nokta koordinatlarını bulun. İlk başta, kendinizi düşünün ve sonra çizimime bakın!

Cevap:

Şimdi Pollogram problemi:

Görev 5: Java-Way-Sia Ver-Shi-na Parale-Le-Lo Gram Ma. Nay-die or-di-on-point.

Bu sorunu iki şekilde çözebilirsiniz: koordinatların mantığı ve yöntemi. İlk önce koordinat yöntemini uyguladım ve sonra size nasıl çözüleceğini söyleyeceğim.

Abscissa noktasının eşit olduğu açıktır. (Noktadan abscissa eksenine göre bir dikeyde yatmaktadır). Düzgün bulmalıyız. Figürümüzün paralel birogram olduğu gerçeğini kullanıyoruz, bu demektir. İki nokta arasındaki mesafe formülünü kullanarak segmentin uzunluğunu bulun:

Partiyi eksenle bağlayın. Kesişme noktası mektubu gösterecektir.

Segmentin uzunluğu eşittir. (Bu anı tartıştığımız görevi buldum), sonra Pitagora teoreminde segmentin uzunluğunu buluruz:

Segmentin uzunluğu - emniyetiyle tam olarak çakışır.

Cevap: .

Başka bir çözüm (sadece onu gösteren bir resim vereceğim)

Çözüm:

1. Davranış

2. Nokta ve uzunluğun koordinatlarını bulun

3. Bunu kanıtlayın.

Bir tane daha kesim uzunluğu sorunu:

Java-Lyube-Sia Ver-Shi-On-Mi Tre-Coal-Ni'nin puanı. Nai di orta çizgisinin uzunluğu, parale lelle.

Üçgenin orta çizgisinin ne olduğunu hatırlıyor musun? Sonra sizin için bu görev ilkokul. Hatırlamazsanız, size hatırlatacağım: Üçgenin orta çizgisi orta karşılıklı tarafları birbirine bağlayan bir çizgidir. Tabana paraleldir ve yarım yarıya eşittir.

Baz bir segmenttir. Daha önce görünmek zorunda kaldığımız uzunluğu eşittir. Sonra orta çizginin uzunluğu yarı daha küçük ve eşittir.

Cevap: .

Yorum: Bu görev, biraz daha sonra döndüğümüz başka bir şekilde çözülebilir.

Bu arada, şimdi birkaç göreviniz var, onlara çıkar, tamamen basit, ancak koordinat yönteminin kullanımında "eli doldurmaya" yardımcı olurlar!

1. Java-LA-SIA Ver-Shi-On-On-On-Tur-Parnasyonun Noktaları. Nai DS çevre çizgisinin uzunluğunu.

2. Noktaları ve Java-Wa-Sia Ver-shi-na Parale-le-lo Gram Ma. Nay-die or-di-on-point.

3. Cut-KA, Co-Unit-NY-Y-TH noktasından NAY-DI uzunluğu ve

4. Co-Or-Di-Nu Flat-CO-PO'sinde Krai-Shan benzeri F-GU-RY'nin NAI.

5. CHA-LE CO-OR-DI-NAT Pro-HO-DIT'de bir fiyat çekimi ile çevreleyen nokta boyunca. Nay-di Onu Ra Di-küf.

6. NAY-DI-DI-DI-DI-SCHIE-NO-POCI, OPI-SAN-NOE ROD-MO-COPSC-NI-KA, VER-SHI-RO-ON-ON-SİZİN CO-VET

ÇÖZÜMLER:

1. Trapeziumun orta çizgisinin tabanın yarısına eşit olduğu bilinmektedir. Baz eşittir ve tabandır. Sonra

Cevap:

2. Bu görevi çözmenin en kolay yolu: BİLDİRİM (paralelogramın kuralı). Vektörlerin koordinatlarını hesaplayın ve mümkün değildir :. Ek olarak, koordinat vektörleri katlanır. Sonra koordinatları var. Aynı koordinatlar ayrıca, vektörün başlangıcı koordinatlarla bir nokta olduğu için bir noktaya sahiptir. Koridor ile ilgileniyoruz. Eşittir.

Cevap:

3. İki nokta arasındaki mesafe formülü tarafından hemen hareket ediyoruz:

Cevap:

4. Resme bakın ve iki figürün gölgeli bölgeyi "kelepçelenmiş" dediği gibi mi? İki kare arasında kelepçelenmiştir. Daha sonra istenen figürün alanı, büyük bir kare eksi kareye eşittir. Kare küçüktür. Küçük bir karenin tarafı bir segment bağlantı noktalarıdır ve uzunluğu eşittir

Sonra küçük kare kare eşittir

Benzer şekilde, büyük bir kare ile: onun tarafı bir segment bağlantı noktalarıdır ve uzunluğu eşittir

Sonra büyük kare kare eşittir

İstediğiniz rakamı formülle bulacaktır:

Cevap:

5. Dairenin bir merkez olarak kökene sahip olması ve noktadan geçerse, yarıçapı tam olarak segmentin uzunluğuna eşit olacaktır (çizim yapın ve neden açık olduğunu anlayacaksınız). Bu segmentin uzunluğunu bulun:

Cevap:

6. Dikdörtgenin yakınında açıklanan çevrenin yarıçapının, diyagonalının yarısına eşit olduğu bilinmektedir. İki köşegenden herhangi birinin uzunluğunu bulacağız (sonuçta, bir dikdörtgende eşittir!)

Cevap:

Her şeyle başa çıktın mı? Bunu çözmek çok zor değildi, çünkü öyle mi? Buradaki kural bir şeydir - görsel bir resim yapabilmek ve tüm verilerden itibaren sadece "saymak".

Biraz bıraktık. Hala kelimenin tam anlamıyla tartışmak istediğim iki nokta var.

Bunun böyle basit bir iş olduğuna karar vermeye çalışalım. İki noktaya ve. Segmentin ortasının koordinatlarını bulun. Bu görevin çözümü aşağıdakilerdir: Noktayı bırakın - Ortayı araması, sonra koordinatlar:

Yani: segmentin ortasının koordinatları \u003d segmentin uçlarının karşılık gelen koordinatlarının aritmetik ortalaması.

Bu kural çok basittir ve bir kural olarak öğrencilerde zorluklara neden olmaz. Hangi görevleri ve nasıl kullanıldığını görelim:

1. NAY-DI OR-DI-ON-TU SE-DI-DI KESİNDEN, KO-UNIT-NY-YU-TH NOKTASI VE

2. Java-Lyube-Sia Ver-Shi-Na-Mi-TWH-Coal-Ni-KA'nın noktaları. Di-on-on-on-on-on-on-on-on-ta noktaları.

3. Nai-di ABS-SU-SU Mahallenin Price-Tra çevresi, Opi-San-SAN Sağ-Mo-Ni-Ka yakınında, ver-shi-ro Co-or-on-on- ot-veteriner.

ÇÖZÜMLER:

1. İlk görev sadece bir klasiktir. Segmentin ortasının tanımına göre derhal hareket ediyoruz. Koordinatları var. Koordinat eşittir.

Cevap:

2. Bu dörtgen bir paralelogram olduğunu görmek kolaydır (hatta eşkenar rhombus!). Kendin kendin kendini kanıtlayabilir, tarafların uzunluğunun hesaplanmasını ve bunları kendi aralarında karşılaştırabilir. Paralelogramlar hakkında ne biliyorum? Çapraz kavşak noktası yarıya bölünür! Evet! Böylece köşegenlerin kesişme noktası ne? Bu, diyagonalların herhangi birinin ortasıdır! Özellikle, diyagonal olarak seçin. Ardından, nokta, koordinat noktasının koordinatlarına eşittir.

Cevap:

3. Daire dikdörtgenin yakınında açıklanan merkezin tesadüfi nedir? Köşegenlerinin kesiştiği noktasıyla çakışıyor. Ve dikdörtgenin köşegeni hakkında ne biliyorsunuz? Onlar eşittir ve kesişme noktası yarıya bölünür. Görev öncekine gitti. Örneğin, diyagonal olarak alacağım. Sonra tarif edilen dairenin merkezi, o zaman orta. Koordinatları arıyor: Aşımsal eşittir.

Cevap:

Şimdi biraz yalnız pratik yap, sadece her görevin cevap vereceğim, böylece kendinizi kontrol edebilirsiniz.

1. NAY-DI-TE-DI-SCHIE-NO-EI, OPI-SAN HAKKINDA TRE-SANI-NI-KA, Ver-Shi-Go-ro

2. NAY-DI-TE-DI-OU-TU-TUR Discileri-NOES, OPI-SAN-SOE PROTAURE-NI-KA, VER-SHI-GO-RO Koordinatları var

3. KA-KO-GO-DI-U-SA, bir fiyat-üçlü ile çevrili olmak gerekir.

4. Eksen ekseninin na-di or-di-on-ta noktaları ve kesimden, ko-birim-yu-th noktası ve

Yanıtlar:

Her şey başardı? Gerçekten umarım! Şimdi - son pislik. Şimdi özellikle özenli olun. Şimdi açıklayacağım malzeme, yalnızca sadece parçanın B'deki koordinat yöntemindeki basit görevler için doğrudan ilişkili değildir, aynı zamanda C2 görevinde her yerde meydana gelir.

Sözlerimden hangisi henüz kısıtlamadım? UNUTMAYAN VEYA NEDEN NEDEN TUTMAK İÇİN VARLIK VE NEDİR? Tam olarak unutmadım mı? Unuttun! Vektörlerin çarpımının ne anlama geldiğini açıklamayı unuttum.

Vektör üzerinde vektör çarpma iki yolu vardır. Seçilen yönteme bağlı olarak, farklı doğanın nesneleriniz olacağız:

Vektör ürünü oldukça cunning yapılır. Nasıl yapılır ve neden gerekli olduğunu, bir sonraki makalede tartışacağız. Ve bu, skaler ürününe odaklanacağız.

Hesaplamamıza izin vermemiz için zaten iki yol var:

Tahmin ettiğin gibi, sonuç aynı olmalı! Yani, ilk önce ilk yolu düşünelim:

Koordinatlar aracılığıyla skaler ürün

Bulun: - Genel olarak bir skaler ürünün kabul edildi

Sonraki hesaplama için formül:

Yani, skaler ürün \u003d vektörlerin koordinatlarının eserlerinin miktarı!

Misal:

Nai di

Karar:

Vektörlerin her birinin koordinatlarını bulacağız:

Skaler ürününü formüle göre hesaplayın:

Cevap:

Görmek, kesinlikle karmaşık bir şey yok!

Şimdi kendimi dene:

· NAY-DI SKA-LAR-NEE, Olayların ve

Başa çıkmak? Belki küçük hileyi fark ettim? Hadi kontrol edelim:

Geçmişte olduğu gibi vektörlerin koordinatları! Cevap:.

Koordinatın yanı sıra, bir skaler ürünü, yani vektörlerin uzunlukları ve aralarındaki kosinüs açısından hesaplamanın başka bir yolu vardır:

Vektörler arasındaki açıyı gösterir ve.

Yani, skaler ürün, aralarındaki köşenin kosinüsündeki vektörlerin uzunluklarının ürününe eşittir.

Neden bu ikinci formüle sahip oluyoruz, eğer birincisi çok daha kolay olan, içinde en azından kosinüs yok. Ve birinci ve ikinci formülden gelen, vektörler arasındaki açıyı nasıl bulacağımız için gerekli olduğu için gereklidir!

Sonra vektörün uzunluğu için formülü hatırlayın!

Sonra bu verileri skaler ürünün formülünde değiştirirsem, alacağım:

Ama diğer tarafta:

Peki sana ne aldım? Artık iki vektör arasındaki açıyı hesaplamanızı sağlayan bir formül var! Bazen aşağıdaki gibi kısalık için de yazılır:

Yani, vektörler arasındaki açıyı hesaplamak için algoritma aşağıdaki gibidir:

1. Skaler ürününü koordinatlardan hesaplar
2. Vektörlerin uzunluğunu buluruz ve onları çeviriyoruz
3. Madde 2'nin sonucunu 2 Madde 2'nin sonucunda bölüyoruz.

Örneklerde pratik yapalım:

1. Köşe, göz kapağı ışını ile arasındaki köşe ve. Gra-du-Sac'a cevabı verin.

2. Önceki görevin şartları altında, vektörler arasında kosiniyi bulun.

Bunu yapacağız: İlk görev karar vermenize yardımcı olacağım ve ikinci kendini yapmaya çalışıyorum! Katılıyorum? Sonra başla!

1. Bu vektör bizim eski tanıdık. Biz zaten skaler işlerini düşündük ve eşitti. Böyle koordinatları var:, Sonra uzunluklarını buluruz:

Sonra vektörler arasında bir kosinüs arıyoruz:

Kosinus hangi köşe eşittir? Bu açıdır.

Cevap:

Şimdi, ikinci görevi çözerim ve sonra karşılaştır! Sadece çok kısa bir karar vereceğim:

2. Koordinatları var, koordinatlar var.

İzin - vektörler arasındaki açı ve sonra

Cevap:

Görevlerin doğrudan vektörde olduğu ve sınav işinin B bölümündeki koordinat yönteminin oldukça nadir olduğu belirtilmelidir. Bununla birlikte, C2 görevlerinin ezici çoğunluğu, koordinat sisteminin tanıtımına başvurarak kolayca çözülebilir. Dolayısıyla, bu makaleyi Vakıf tarafından, karmaşık işleri çözmek için gerekli olacak kadar zorlu inşaat yapacağımız temelinde düşünebilirsiniz.

Koordinatlar ve vektörler. Orta fitil

Koordinat yöntemini incelemeye devam ediyoruz. Son bölümde, izin veren bir dizi önemli formül getirdik:

1. Vektörin koordinatlarını bulun
2. Vektör uzunluğunu bulun (alternatif: iki nokta arasındaki mesafe)
3. Katlayın, top vektörleri çıkarın. Onları gerçek numaraya çarp
4. Orta kesim bulmak
5. Vektörlerin skaler ürününü hesaplar
6. Vektörler arasında açı bulmak

Tabii ki, tüm koordinat yöntemi bu 6 puana uymuyor. Bu tür bilimin üniversiteyi tanımak zorunda olduğunuz analitik bir geometri olarak azalır. Sadece tek bir durumda sorunları çözmenize izin verecek bir temel oluşturmak istiyorum. Sınav. B bölümünün görevleri ile şu anda net bir şekilde yeni bir seviyeye gitme zamanı! Bu makale, koordinat yöntemine taşınması makul olacağı C2 görevlerini çözme yöntemine ayrılacaktır. Bu rasyonalite, görevin bulması ve hangi figürün verilmesi gerektiği gerçeğiyle belirlenir. Böylece, eğer verilirse koordinat yöntemini uygulayacağım:

1. İki uçak arasındaki açı bulun
2. Düz ve düzlem arasındaki açıyı bulun
3. İki düz arasındaki açıyı bulun
4. Noktadan uçağa olan mesafeyi bulun
5. Noktadan direkt mesafeyi bulun
6. Satırdan uçağa olan mesafeyi bulun
7. İki düz arasındaki mesafeyi bulun

Sorunun durumundaki şekil, rotasyonun gövdesidir (top, silindir, koni ...)

Koordinat yöntemi için uygun rakamlar şunlardır:

1. Dikdörtgen paralelpiped
2. Piramit (üçgen, dörtgen, altıgen)

Ayrıca benim deneyimimde koordinat yöntemini kullanmak için pratik değildir.:

1. Bölüm alanları arıyor
2. Hacim hesaplamaları

Bununla birlikte, uygulamadaki koordinat durumu için üç "kâr edilemeyen" üçünün oldukça nadir olduğu belirtilmelidir. Çoğu görevde, özellikle üç boyutlu binalarda (bazen oldukça karmaşık) çok güçlü değilseniz, kurtarıcınız olabilir.

Yukarıdaki rakamlar nelerdir? Artık düz değiller, örneğin bir kare, üçgen, daire ve toplu! Buna göre, iki boyutlu değil, üç boyutlu bir koordinat sistemi olmadığını düşünmemiz gerekir. Oldukça kolaydır: Abscissa'nın ekseninin yanı sıra, başka bir eksen, aplike ekseni tanıtıyoruz. Şekil şematik olarak karşılıklı konumlarını gösterir:

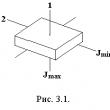
Hepsi karşılıklı olarak dik, bir noktada kesişir, bu da koordinatların başlangıcını arayacağımız. Abscissa'nın ekseni, daha önce olduğu gibi, koordinatın eksenini - ve uygulamanın tanıtılan eksenini gösteririz.

Daha önce, uçağın üzerindeki her nokta iki sayı ile karakterize edildi - abscissa ve sıradan, daha sonra uzaydaki her nokta zaten üç sayı ile tanımlanmıştır - Abscissa, Koridor, Appikate. Örneğin:

Buna göre, noktanın apscissa eşittir, koordinat - ve başvurumlar -.

Bazen Abscissa Noktası ayrıca abscissa ekseni üzerindeki noktanın projeksiyonu, koordinat - koordinat ekseni üzerindeki noktanın projeksiyonu ve uygulama - aplike ekseni üzerindeki noktanın projeksiyonu. Buna göre, eğer nokta ayarlanırsa, koordinatlarla ilgili nokta:

projeksiyon noktasını uçağa çağırın

projeksiyon noktasını uçağa çağırın

Doğal soru ortaya çıkar: Tüm formüller alanda iki boyutlu bir durum için türetilmiş midir? Cevap olumlu, onlar adil ve aynı görünüme sahip. Küçük bir detay için. Sanırım hangisinin için kendini tahmin ettin. Tüm formüllerde, Aplike ekseninden sorumlu başka bir üye eklemeliyiz. Yani.

1. İki nokta ayarlandıysa: o zaman:

• Vektörin koordinatları:
• İki nokta arasındaki mesafe (veya vektörün uzunluğu)
• Segmentin ortasında koordinatlar var

2. İki versiyon verilirse: ve sonra:

• Skaler ürünleri:
• Vektörler arasında kosinüs açısı:

Ancak, alan çok basit değil. Anladıkça, başka bir koordinat eklemek, bu alandaki "yaşayan", rakamların spektrumunda önemli bir çeşitlilik yapar. Ve daha fazla anlatım için, bazı, kabaca konuşmayı "genelleme" düzleştirmem gerekiyor. Bu "genelleme" uçak olacaktır. Uçak hakkında ne biliyorsun? Soruyu cevaplamaya çalışın ve bir uçak nedir? Söylemesi çok zor. Ancak, hepimiz sezgisel olarak nasıl göründüğünü hayal ediyoruz:

Kabaca konuşursak, bu, uzayda kaplı sonsuz olmayan bir "yaprak". "Sonsuzluk", uçağın her yöne uygulandığı anlaşılacağı anlaşılmalıdır, yani alanı sonsuzluğa eşittir. Bununla birlikte, "parmaklardaki" bu açıklama, uçağın yapısı hakkında en ufak bir fikri vermez. Ve onunla ilgilenecek.

Geometri ana eksenlerinden birini hatırlayalım:

• düzlemdeki iki farklı noktadan, düz gider, sadece bir tane ile gider:

Veya uzayda analogu:

Tabii ki, denklemin önceden belirlenmiş iki noktada doğrudan nasıl çıkarılacağını hatırlıyorsunuz: Birinci nokta koordinatları varsa: ve ikincisi, doğrudan denklem aşağıdaki gibi olacaktır:

7. sınıfta geçtiğin. Uzayda, doğrudan denklem şöyle görünür: Koordinatlarla iki nokta verelim: denklem düzdür, geçerken, görünüşe sahiptir:

Örneğin, noktalar yoluyla, düz çizgi geçer:

Nasıl anlaşılmalıdır? Bu şu şekilde anlaşılmalıdır: Koordinatları aşağıdaki sistemi memnun ederse, nokta sınırda yatıyor:

Gerçekten denklem ile ilgilenmeyeceğiz, ancak doğrudan vektörlerin çok önemli bir kavramına dikkat etmeliyiz. - Bu doğrudan ya da paralel olarak yatan herhangi bir sıfır vektör.

Örneğin, her iki vektör de doğrudan rehber vektörlerdir. Noktayı çizgiye ve kılavuz vektörüne bırakın. Daha sonra Denklem doğrudan aşağıdaki formda yazılabilir:

Bir kez daha tekrar ediyorum, denklemle çok ilgilenmeyeceğim, ancak rehber vektörün ne olduğunu hatırlamanıza gerçekten ihtiyacım var! Tekrar: bu, düz bir çizgi üzerinde yatan veya paralel olan herhangi bir saçma vektörüdür.

Görüntüle düzlemin belirtilen üç nokta için denklemi Çok önemsiz değil ve genellikle bu soru lisenin farkında değil. Ve boşuna! Bu teknik, karmaşık görevleri çözmek için koordinat yöntemine başvururken hayati öneme sahiptir. Ancak, yeni bir şey öğrenmek için arzu dolu olduğunuzu varsayıyorum? Ayrıca, zaten analitik geometri sırasında genellikle incelenen bir tekniğe sahip olduğunuzu zaten bildiğiniz zaman öğretmeninize vurgulayabilirsiniz. Öyleyse devam et.

Düzlem denklemi, uçaktaki doğrudan denklemden çok farklı değil, yani görünüyor:

bazı sayılar (hepsi eşit değil) ve değişkenler, örneğin: vb. Gördüğünüz gibi, düzlemin denklemi düz çizginin denkleminden (doğrusal fonksiyon) çok farklı değildir. Ancak, sizinle tartıştığımızı hatırlıyor musun? Bir düz çizgide yatan üç noktamız varsa, uçağın denklemi kesinlikle onlar tarafından restore edilir. Ama nasıl? Sana açıklamaya çalışacağım.

Uçak denklemi:

Ve puanlar bu düzleme aittir, daha sonra her noktanın koordinatlarını uçak denklemine ikame ederken, gerçek bir kimlik almalıyız:

Böylece, bilinmeyen üç denklemi çözmek için gerekli olur! İkilem! Bununla birlikte, her zaman (bunun için bölmeniz gereken) olduğu varsayılabilir. Böylece, üç bilinmeyen üç denklem elde ediyoruz:

Ancak, böyle bir sistemi çözmeyeceğiz ve bizden gelen gizemli ifadeyi yönlendireceğiz:

Üç ayar noktasından geçen uçağın denklemi

\\ [\\ Sol | (\\ başlar (dizi) (* (20) (c)) (x - (x_0)) ve ((x_1) - (x_0)) & ((x_2) - (x_0)) \\\\ (y - (y_0) ) & ((y_1) - (y_0)) & ((Y_2) - (y_0)) \\\\ (z - (z_0)) & (((z_1) - (z_0)) & (((z_2) - (z_0)) \\ End (dizi)) \\ sağ | \u003d 0 \\]

Dur! Başka ne? Bazı çok sıradışı bir modül! Ancak, önünde gördüğünüz nesne, modülle ilgisi yoktur. Bu nesnenin üçüncü derecede belirleyici olarak adlandırılır. Bundan sonra, gelecekte, uçaktaki koordinat yöntemiyle uğraştığınızda, bu tanımlamaları çok sık karşılaşacaksınız. Üçüncü derecede belirleyici nedir? Garip bir şekilde, sadece bir sayıdır. Özellikle sayının belirleyiciyle karşılaştıracağımızın ne olduğunu anlamak istiyor.

İlk önce üçüncü sipariş belirleyiciyi daha genel bir biçimde yazalım:

Bazı sayılar nerede. Ve ilk endeks altında, satır numarasını ve dizinin altında - sütunun sayısı. Örneğin, bu sayının ikinci satırın ve üçüncü sütunun kesişiminde olduğu anlamına gelir. Aşağıdaki soruyu yükseltelim: Böyle bir belirleyiciyi nasıl hesaplayacağız? Yani, onu hangi özel numarayı karşılaştıracağız? Üçüncü derecede bir belirleyici için, heuristic (görsel) bir üçgen kuralı var gibi görünüyor:

1. Ana çaprazın elemanlarının (sol üst köşeden alt sağa), "dik" ana çapraz köşegen olan elementlerin ürünü olan elementlerin ürünü, ikinci üçgen "dik" ana çaprazını oluşturan elementlerin ürünü
2. Yan çapraz elemanların ürünü (alt soldan soldan soldan soldan), "dik) ilk üçgeninin" dik olarak "oluşturan elementlerin ürünü," dikey "yan diyagonal olan ikinci üçgen" dik) elementlerin ürünü
3. Daha sonra belirleyici, adımda elde edilen değerlerin farkına eşittir ve

Tüm bu numaraları yazarsanız, aşağıdaki ifadeyi alacağız:

Bununla birlikte, bu formdaki hesaplama yöntemini hatırlamak gerekli değildir, sadece üçgenleri ve fikri korumak için yeterlidir, bu da yaptığı şeydir ve daha sonra bir şeyden ne kesilir).

Örnekte üçgen yöntemini gösterelim:

1. Belirleyici'yi hesaplayın:

Neye katlandığımızla uğraşalım ve ne - çıkardık:

"Plus" ile giden bileşenler:

Bu ana çaprazdır: elementlerin ürünü eşittir

İlk üçgen, "dik ana çapraz köşegen: elemanların ürünü eşittir

İkinci üçgen, "dik ana çapraz köşegen: elemanların ürünü eşittir

Üç sayıyı katlıyoruz:

"Eksi" ile giden bileşenler

Bu bir yan çaprazdır: elemanların ürünü eşittir

"Yana dik dikey" ilk üçgeni: elemanların ürünü eşittir

İkinci üçgen, "tarafa dik dikey: elementlerin ürünü eşittir

Üç sayıyı katlıyoruz:

Yapılacak olan tek şey, "bir artı" teriminin "bir eksi ile" teriminin toplamından mahrum etmektir:

Böylece,

Gördüğünüz gibi, üçüncü derecede belirleyicilerin hesaplanmasında karmaşık ve doğaüstü bir şey yoktur. Üçgenleri hatırlamak ve aritmetik hatalara izin vermemek sadece önemlidir. Şimdi kendinizi hesaplamaya çalışın:

Kontrol:

1. İlk üçgen, dik ana çapraz diyagonal:
2. İkinci üçgen, dik ana çapraz diyagonal:
3. Bir artı ile terimlerin miktarı:
4. Yan köşegenlere dik olan ilk üçgen:
5. İkinci üçgen, yan köşegenlere dik:
6. Eksi ile olan şartların miktarı:
7. Artı eksi olan bileşenlerin miktarı eksi ile olan şartların miktarını:

İşte bir başka determinants, anlamlarını kendi başlarına hesapladılar ve cevaplarla karşılaştırdılar:

Yanıtlar:

Herşey çakıştı mı? Harika, sonra devam edebilirsiniz! Eğer zorluklar varsa, konsey benimdir: determinant çevrimiçi olarak hesaplamak için bir grup yazılım var. İhtiyacınız olan tek şey tanımlayıcınızla gelmek, kendiniz hesaplamak ve ardından programın ne düşüneceği ile karşılaştırın. Ve sonuçlar tesadüfin başlamadığı sürece. Bu an beklemek için uzun süre beklemeyeceğinden eminim!

Şimdi, üç ayar noktasından geçen uçağın denklemi hakkında konuştuğumda kimin yazdığım belirleyiciye geri dönelim:

İhtiyacınız olan tek şey, değerini doğrudan (üçgenler yöntemiyle) hesaplamak ve sonucu sıfıra eşitlemektir. Doğal olarak, çünkü - değişkenler, o zaman onlara bağlı olarak bir ifade alacaksınız. Bir düz çizgide yatan üç ayar noktadan geçen bir uçağın denklemi olacak bu ifadedir!

Yukarıda belirtilen örneği gösterelim:

1. Noktalardan geçen uçağın denklemini oluşturun

Bu üç nokta için belirleyiciyi yazıyoruz:

Basitleştirmek:

Şimdi doğrudan üçgenlerin kuralına göre hesaplıyoruz:

\\ [(\\ Sol | (\\ başlar (dizi) (* (* (20) (c)) (x + 3) & 2 & 6 \\\\ (y - 2) & 0 & 1 \\ (z + 1) & 5 0 \\ End (dizi)) \\ sağ | \u003d \\ sol ((x + 3) \\ sağ) \\ CDOT 0 \\ CDOT 0 + 2 \\ CDOT 1 \\ CDOT \\ Sol ((Z + 1) \\ sağ) + \\ Sol ( (Y - 2) \\ sağ) \\ CDOT 5 \\ CDOT 6 -) \\]

Böylece, noktalardan geçen düzlemin denklemi formu vardır:

Şimdi bir görevi kendi başınıza çözmeye çalışın ve sonra tartışacağız:

2. Noktalardan geçen uçağın denklemini bulun

Peki, şimdi kararını tartışalım:

Belirleyici yapıyoruz:

Ve değerini hesaplar:

Sonra uçağın denklemi:

Ya da kısalmak, biz:

Şimdi kendi kendine kontrol için iki görev:

1. Üç noktadan geçen uçağın denklemini oluşturun:

Yanıtlar:

Hepsi çakıştı mı? Yine, belirli zorluklar varsa, öyleyse tavsiyem: Kafamdan üç puan alırsınız (büyük bir olasılıkla düz bir olasılıkla bir düzeyde yatmayacaklar), üzerlerine bir uçak oluşturun. Ve sonra kendinizi çevrimiçi olarak kontrol edin. Örneğin, sitede:

Ancak, belirleyicilerin yardımıyla, sadece uçağın denklemini oluşturacağız. Unutma, size vektörlerin sadece Skaler ürününü tanımlamadığını söyledim. Hala bir vektörün yanı sıra karışık bir iş var. Ve eğer iki vektörün skaler ürünü ve bir sayı olacaksa, sonra iki vektörün vektör ürünü olacak ve vektör olacaktır ve bu vektör belirtilenlere dik olacaktır:

Ayrıca, modülü, vektörlerin öncesinde ve bunlardan önce olan paralelogram alanına eşit olacaktır. Bu vektörün noktadan doğrudan olduğu mesafeyi hesaplaması gerekecektir. Vektörlerin vektör ürününü nasıl düşünürüz ve, eğer koordinatları ayarlanmışsa? Üçüncü derecede belirleyici kurtarmaya gelir. Ancak, vektör sanatını hesaplamak için algoritmaya devam etmeden önce, küçük bir lirik retleme yapmalıyım.

Bu geri çekilme temel vektörleriyle ilgilidir.

Şematik olarak, resimde tasvir edilirler:

Ne düşünüyorsun, neden temel olarak adlandırıyorlar? Gerçek şu ki :

Veya resimde:

Bu formülün adaleti açıktır, çünkü:

Vektör sanat

Şimdi bir vektör çalışmanın tanıtımına devam edebilirim:

İki vektörün vektör ürünü, aşağıdaki kural tarafından hesaplanan vektör olarak adlandırılır:

Şimdi vektör sanat hesaplamasının birkaç örneğini verelim:

Örnek 1: Bul Vektör Vektör çizimleri:

Çözüm: Belirleyiciyi oluşturur:

Ve hesaplamak:

Şimdi Temel Vektörler ile yazmaktan, vektörün olağan kaydına geri döneceğim:

Böylece:

Şimdi dene.

Hazır? Kontrol:

Ve geleneksel olarak iki kontrol için görevler:

1. Vektör küçük resim bulmak:
2. Vektör küçük resim bulmak:

Yanıtlar:

Üç vektörün karışık ürün

Bana ihtiyacı olan son tasarım, üç vektörün karışık bir üründür. Skaler yanı sıra bir sayıdır. Hesaplamanın iki yolu var. - belirleyiciden, - karışık bir işle.

Yani, üç versiyonumuz var:

Daha sonra gösterilen üç vektörün karışık ürünü, aşağıdaki gibi hesaplanabilir:

1. - Yani, karışık bir ürün, diğer iki vektörün bir vektör ürünü üzerinde bir vektörün skaler bir ürünüdür.

Örneğin, üç vektörün karışık bir ürünü:

Bağımsız bir şekilde bir vektör ürünü aracılığıyla hesaplamaya çalışın ve sonuçların eşleşeceğinden emin olun!

Ve yine - kendi kendine çözümler için iki örnek:

Yanıtlar:

Koordinat sistemini seçin

Şimdi, geometride karmaşık stereometrik işleri çözmek için gerekli tüm bilgi temeli var. Bununla birlikte, doğrudan kararlarının örneklerine ve algoritmalarına geçmeden önce, hangi soruyu şu konuda durmanın yararlı olacağına inanıyorum: belirli bir rakam için koordinat sistemini seçin. Sonuçta, koordinat sisteminin karşılıklı konumu seçimi ve uzaydaki figür nihayetinde hantal hesaplamaların ne kadar zahmetli olacağını belirler.

Size bu bölümde aşağıdaki rakamları göz önünde bulundurduğunu hatırlatıyorum:

1. Dikdörtgen paralelpiped
2. Doğrudan Prizma (Üçgen, Altıgen ...)
3. Piramit (üçgen, dörtgen)
4. Tetrahedron (bir ve üçgen piramit ile aynı)

Dikdörtgen paralelepipeda veya küp için, yapmanızı öneririz:

Yani, "açıya" koyacağım. Küp ve paralelepipli çok iyi rakamlardır. Onlar için, köşelerinin koordinatlarını her zaman kolayca bulabilirsiniz. Örneğin, eğer (Şekilde gösterildiği gibi)

vertic'lerin koordinatları aşağıdaki gibidir:

Tabii ki, elbette, bir küp veya dikdörtgen paralellemeye sahip olmanın nasıl daha iyi olduğunu hatırlamanıza gerek yoktur - tercihen.

Doğrudan prizma

Prizma daha zararlı bir figürdür. Uzayda bulunan farklı olabilir. Ancak, benim için en çok kabul edilebilir görünüyordum:

Üçgen prizma:

Yani, üçgenin yanlarından bir tanesi ekseni yerleştirdik ve köşelerden biri koordinatların başlangıcıyla çakışıyor.

Altıgen Prizma:

Yani, köşelerden biri koordinatların başlangıcıyla çakışıyor ve taraflardan biri eksende yatıyor.

Dörtgen ve altıgen piramit:

Durum, Küba'ya benzer: tabanın iki yüzü, koordinat eksenleriyle birlikte, koordinatların başlangıcıyla birleştirdiğimiz köşelerden biri. Sadece küçük karmaşıklık, noktanın koordinatlarını hesaplar.

Altıgen piramit için - bir altıgen prizma için benzer şekilde. Ana görev, tepe sahasının koordinatlarını aramada tekrar.

Tetrahedron (üçgen piramit)

Durum, üçgen bir prizma için liderlik ettiğime çok benzer: Bir tepe, koordinatların başlangıcıyla çakışıyor, bir taraf koordinat ekseninde yatıyor.

Şimdi, nihayet sorunları çözmek için yaklaşıyoruz. Maddenin başında söylediklerimden, bu sonuca koyabilirsin: Çoğu C2 görevi 2 kategoriye ayrıldı: mesafe başına açı ve görevlerde zorluklar. İlk başta, açıyı bulma görevlerini göz önünde bulunduracağız. Bunlar, aşağıdaki kategorilere ayrılırlar (karmaşıklık arttıkça):

Köşeleri aramak için görevler

1. İki düz arasındaki açıyı bulmak
2. İki uçak arasındaki açı bulmak

Bu görevleri tutarlı bir şekilde düşünelim: İki düz arası açıyı bularak başlayalım. İyi, hatırla ve daha önce benzer örneklerle karar verdik mi? Hatırlıyorum, çünkü böyle bir şeyimiz vardı ... iki vektör arasındaki açı arıyorduk. İki versiyon verildiğinde size hatırlatacağım: ve aralarındaki köşe oranıdır:

Şimdi bir hedefimiz var - iki düz arasında bir açı bulma. "Düz resme" dönelim:

Köşeler iki düz çizginin kesişimi ile ne kadar yaptı? Zaten parçalar. Gerçek şu ki, onlardan sadece iki ondan eşit değil, diğerleri onlar için dikey (ve bu nedenle onlarla çakışıyorlar). Peki, iki düz arasında bir açı olarak ne tür bir açı kabul edilmelidir? İşte bir kural: İki doğrudan arasındaki açı her zaman dereceden fazla değil. Yani, iki açıdan, her zaman en küçük dereceye sahip bir açı seçeceğiz. Yani, bu resimde, iki düz arasındaki açı eşittir. İki açının en küçüğü için bir aramaya uğratmamak için, modülü kullanmayı teklif ettiler. Böylece, iki doğrudan arasındaki açı, formül tarafından belirlenir:

Siz, dikkatli bir okuyucu gibi, soruyu uyandırmak zorunda kaldı: Nerede, aslında, köşenin kosinüsünü hesaplamamız gereken en çok sayıları alacağız? Cevap: Onları doğrudan vektörlerden alacağız! Böylece, iki düz çizgi arasında bir açı bulmak için algoritma aşağıdaki gibidir:

1. Formula 1'i uyguluyoruz.

Veya daha ayrıntılı olarak:

1. İlk doğrudan rehber vektörünün koordinatlarını arıyoruz
2. Kılavuz vektörün koordinatlarını ikinci direkt olarak arıyoruz
3. Skaler ürünlerinin modülünü hesaplar
4. İlk vektörün uzunluğunu arıyorum
5. İkinci vektörün uzunluğunu arıyorum
6. Paragrafın (4) paragrafının sonuçları üzerindeki sonuçlarını çarpın.
7. Paragraf 3'in sonucunu 6. fıkra sonucunda böldük. Doğrudan arasındaki açının kosinüsünü alıyoruz.
8. Bu sonuç açının doğru bir şekilde hesaplanmasına izin verirse, arıyoruz
9. Aksi halde arquosine içinden yazıyoruz

Şimdi, görevlere geçme zamanı: İlk ikisinin çözümü detaylı olarak göstereceğim, kısa halde başka bir karar vereceğim ve sadece son iki göreve cevap vereceğim, tüm hesaplamaları harcamalısınız onlara.

Görevler:

1. Pra-Ville-Nome TET-RA-ED-GEA NAI DI, SO-CO-TET-RA-RA-RA ve MEA-DI-BO-KO koordinatları arasındaki köşede.

2. Pra-Ville-Neu-Kömür Pi-Ra-Mi-de Stro-ROS'da OS-Na-Viya eşittir ve kaburga buketi eşittir, düz olarak köşeyi döner.

3. Pra-Ville Che-You-Rah-kömür PI-RA-MI'nin tüm kaburgalarının uzunlukları birbirine eşittir. NAI-di Doğrultalar ile RE-ZOK'tan sonra açı - Pi-Ra-Mi-DWI verilen eş-tek başına, nokta Se-Re-di-Onun Buketi Kaburga

4. Küpün kenarında, nokta başına bir noktada, böylece NAI-DI, doğrudan köşeyi

5. Point - SE-RE-di-on kenarları Küba NAI-di düz ila doğrudan köşe.

Görevleri bu sırada yanlış anladım. Koordinat yönteminde gezinmeye başlamak için zamanınız olmadığı zaman, kendimi en "sorunu" rakamları söküyorum ve en basit küple başa çıkmanızı sağlayacaksınız! Yavaş yavaş, tüm rakamlarla çalışmayı öğrenmelisiniz, görevlerin karmaşıklığı konudan konuya kadar artacağım.

Sorunları çözmeye devam ediyoruz:

1. Bir tetrahedron çizin, daha önce tasarladığım şekilde koordinat sistemine koyun. Tetrahed doğru olduğundan - sonra tüm yüzleri (baz dahil) - sağ üçgenler. Yan tarafın uzunluğu verilmediğinden, o zaman eşit alabilirim. Bence açının gerçekten tetrahedronumuzun nasıl "gerileyeceğine" bağlı olmayacağını anladığını düşünüyorum. Ayrıca Tetrahedra yüksekliğinde ve medyanda da geçirir. Yol boyunca, üssünü boyadım (ayrıca kullanışlı olacak).

A ile arasındaki açıyı bulmam gerekiyor. Biz ne biliyoruz? Sadece nokta koordinatını biliyoruz. Böylece, puanların daha fazla koordinatını bulmak gerekir. Şimdi düşünüyoruz: Nokta, üçgenin yüksekliklerinin (veya bisetriss veya ortanca) kesişme noktasıdır. Ve nokta yükseltilmiş bir nokta. Nokta, segmentin ortasıdır. Sonra kesin olarak bulmalıyız: Puanların koordinatları :.

En basitiyle başlayalım: noktanın koordinatları. Şekillere bakın: Noktadaki noktasının sıfır olduğu açıktır (nokta düzlemde yatıyor). Koridoruna eşittir (ondan beri - ortanca). Abscissa bulmak daha zordur. Ancak, Pythagora teoremi temelinde kolayca yapılır: bir üçgen düşünün. Hipotenüsü eşittir ve katetlerden biri daha sonra eşittir:

Sonunda biz var :.

Şimdi noktanın koordinatlarını buluyoruz. Appliquet'in tekrar sıfır olduğu açıktır ve koordinatı, bu nokta ile aynıdır. Onun abscissa bul. Bu, bunu hatırlarsanız, önemsizce yapılır. kavşak noktasının eşkenar üçgeninin yükseklikleri orantılı olarak bölünmüştür., üstten saymak. :, Sonra, segmentin uzunluğuna eşit istenen abscissa noktası eşittir:. Böylece, noktanın koordinatları eşittir:

Noktanın koordinatlarını bulun. Abscissa ve koordinatının apsis ve sıradan bir noktayla çakıştığı açıktır. Ve başvuru, segmentin uzunluğuna eşittir. - Bu, üçgenin katlarından biridir. Üçgen hipotenüs, bir kesimdir - katat. Cesur bir vurguladığım nedenlerden dolayı arıyor:

Nokta, segmentin ortasıdır. O zaman segmentin ortasındaki koordinatların formülünü hatırlamamız gerekir:

Hepsi, şimdi rehber vektörlerin koordinatlarını arayabiliriz:

Her şey hazır: Formüldeki tüm verileri değiştiriyoruz:

Böylece,

Cevap:

Böyle bir "korkutucu" cevapları korkutmamalısınız: C2 görevleri için ortak uygulama. Bu bölümdeki "güzel" cevabını şaşırtmayı tercih ederim. Ayrıca, belirttiğiniz gibi, Pythagoreo teoremi ve eşkenar üçgen yüksekliklerinin mülkü dışında, pratik olarak hiçbir şeye başvurmadım. Yani, stereometre görevini çözmek için, minimum stereometreyi kullandım. Kısmen bu kısmen "söndürme" içindeki kazanç oldukça hacimli bir bilgi işlemdir. Ama onlar yeterince algoritma!

2. Koordinat sistemi ile birlikte doğru altıgen piramit göstereceğim:

Düz olarak açıyı bulmalıyız. Böylece, görevimiz puanların koordinatları için aramaya indirgenir :. Son üçün koordinatları küçük bir düzende bulacağız ve köşelerin koordinatını nokta koordinatı ile bulacağız. Toplu olarak çalışır, ancak başlamanız gerekir!

a) Koordinat: Uygulamasının ve koordinatının sıfıra eşit olduğu açıktır. Abscissa'yı buluruz. Bunu yapmak için dikdörtgen bir üçgen düşünün. Ne yazık ki, biz sadece eşit olan hipotenüs ile tanınırız. Watch bulmaya çalışacağız (bunun için kategorinin en çok uzunluğunun bize apcissue noktası vereceği açıktır). Onu nasıl arıyoruz? Piramidin tabanında yattığımız şekilde bunu hatırlayalım. Bu doğru altıgen. Bu ne anlama geliyor? Bu, tüm taraflara sahip olduğu ve tüm köşelerin eşit olduğu anlamına gelir. Böyle bir açı bulmak gerekir. Herhangi bir fikir? Fikirler kitlesi, ancak bir formül var:

Doğru N-Parlamentonun köşelerinin toplamı eşittir. .

Böylece, doğru altıgenin açılarının toplamı derecelere eşittir. Sonra köşelerin her biri eşittir:

Resme tekrar bakıyoruz. Kesim - bisektör açısının olduğu açıktır. Sonra açı derecelere eşittir. Sonra:

Sonra, nerede.

Böylece koordinatları var

b) Şimdi koordineyi kolayca bulabilirsiniz :.

c) Noktanın koordinatlarını bulacağız. Abscissa, segmentin uzunluğuyla çakıştığından, eşittir. Koridorunu bulmak çok zor değil: Eğer noktaları bağlarsak ve doğrudan belirlemenin kesişme noktasını bağlarsak, söyleyelim. (Basit bir yapının kendisi yapın). Öyleyse, BOURNINAL NOKTA B, segmentlerin uzunluklarının toplamına eşittir. Üçgene tekrar dön. Sonra

Öyleyse çünkü o zaman nokta koordinatları var.

d) Şimdi noktanın koordinatlarını bulacağız. Bir dikdörtgen düşünün ve bu şekilde koordinatları kanıtlayın:

e) Köşelerinin koordinatlarını bulmak için kalır. Abscissa ve koordininin apsis ve sıradan bir noktayla çakıştığı açıktır. Başvuranı buluruz. O zamandan beri. Dikdörtgen bir üçgen düşünün. Sorunun durumuna göre, yan kenar. Bu, üçgenimin hipotenüsüdür. Sonra piramitin yüksekliği - Catat.

Sonra nokta koordinatları vardır:

Her şey, benim için tüm ilgi çekici yerlerin koordinatlarına sahibim. Doğrudan doğrudan vektörlerin koordinatlarını arıyorum:

Bu vektörler arasında bir açı arıyoruz:

Cevap:

Yine, bu görevi çözerken, doğru N-karenin köşelerinin, yanı sıra kosinüsün tanımı ve dikdörtgen üçgenin sinüsünün formülü dışında herhangi bir düzensiz teknik kullanmadım.

3. Yine piramitteki kaburgaların uzunluğu verilmemdiğinden, o zaman bunları birine eşit olarak göreceğim. Böylece, tüm kaburgalar sadece yan değil, birbirlerine eşittir, daha sonra piramitin tabanında ve kare yalan söylüyor ve yan yüzler sağ üçgenlerdir. Bu piramitin yanı sıra uçaktaki tabanını, görevin metninde belirtilen tüm verileri göstereceğiz:

A ile arasındaki açı arıyoruz. Puan koordinatlarını aradığımda çok kısa hesaplamalar yapacağım. Onları "deşifre etmek" gerekir:

b) - segmentin ortası. Koordinatları:

c) Üçgende Pythagora teoreminde bulacağım uzunluğu kes. Üçgende Pisagor teoreminde bulacağım.

Koordinatlar:

d) - segmentin ortası. Koordinatları eşittir

e) vektör koordinatları

f) vektör koordinatları

g) Bir açı arıyoruz:

Küp en basit şekildedir. Onunla kendinle başa çıkacağına eminim. Görevlerin 4 ve 5'in cevapları aşağıdaki gibidir:

Düz ve düzlem arasındaki açıyı bulmak

Peki, basit görevlerin zamanı bitti! Şimdi örnekler daha da zor olacak. Düz ve uçak arasındaki köşeyi bulmak için aşağıdaki gibi olacağız:

1. Üç puan ile bir uçak denklemi inşa ediyoruz
   ,
   Üçüncü sipariş belirleyiciyi kullanarak.
2. İki puan ile doğrudan bir rehber koordinat arıyoruz:
3. Formülü, düz ve düzlem arasındaki açıyı hesaplamak için kullanıyoruz:

Gördüğünüz gibi, bu formül iki düzlük arasında köşeleri aramak için kullandığımız gerçeğine çok benzer. Doğru parçanın yapısı sadece aynıdır ve şimdi şimdi olduğu gibi kosinüs değil şimdi sinüs arıyoruz. Peki, bir zıt eylem eklendi - uçağın denklemini arar.

Uzun bir kutuda ertelemeyelim Örneklerin Çözümü:

1. Os-no-va-ni-it Raughty-na-de-re-kömür takma adı çok da bir ödül eşit düz temin etmek durumundadır-lap-ben-SMTA olduğunu. Nay-di, düz ve düz co-st arasındaki köşe

2. Doğrudan-MO-MR. PA-RAL-LES-LE-PI-DE-DIE-DIE-LES-LE-PI-DIE-DI-LEVEL-CO arasındaki-

3. Pra-Ville'de, boynu kömürü ödüllü tüm kaburgalar eşittir. Nai-di, düz ve düz co-st arasındaki köşe.

4. Pra-ville Tre-Kömür Pi-Ra-Mi-de Os-no-Va Ni Batı-Na-di-hırsız, Obra-Zo-Wan düz-ko-ko-kopya ile Os-no- VA ve düz, RE-Di kaburgalarından ve

pra-Vll-ote dört doğan Pi-Ra-Mi-dy her kaburga 5. uzunlukları birbirine eşittir. NAY-DI Nokta CE-RE-DI-ON-ON-CO-RIB PI-RA-MI-DY ise, düz ve düz ortak yahnilik arasındaki açı.

kısaca ve bağımsız karar için son iki izni siz - Yine, ayrıntılı olarak ilk iki görevi, üçüncü karar verecektir. Buna ek olarak, zaten üçgen ve dörtgen piramitler uğraşmak zorunda ama prizmalarla var - Şimdiye kadar hiç yoktur.

ÇÖZÜMLER:

1. Bir prizma ve tabanını göster. Koordinat sistemi ile uyumludur ve Terk durumunda verilen tüm verileri not edin:

O oranlara uygun olmayan bazı uyumsuzluklardan dolayı özür dilerim, ancak sorunu çözmek için esasen çok önemli değil. Uçak sadece prizmanın "arka duvarı". Sadece böyle bir uçağın denkleminin şöyle olduğunu tahmin etmek yeterlidir:

Ancak, doğrudan gösterilebilir:

Bu düzlemde rastgele üç puan seçin: Örneğin,.

Bir uçak denklemi yapın:

Size egzersiz yapın: bağımsız olarak bu belirleyiciyi hesaplayın. Başardın mı? Sonra uçağın denklemi:

Ya da sadece

Böylece,

Örneği çözmek için, kılavuz vektörün koordinatlarını düz bulmam gerekiyor. nokta koordinatlarının başlangıcı ile düşmüş olduğundan, vektör koordinatları sadece çakıştığı için bu noktanın koordinatları ile biz noktasının koordinatlarının başında bulacaksınız.

Bunu yapmak için bir üçgen düşünün. Yüksekliği (ortanca ve bisektördür) üstten geçireceğiz. O zamandan beri, koordinat noktası eşittir. Bu noktanın abscissa'sını bulmak için, segmentin uzunluğunu hesaplamamız gerekir. Pythagora teoremine göre, biz var:

Sonra nokta koordinatları vardır:

Nokta, noktaya "yükseltildi":

Sonra vektörün koordinatları:

Cevap:

Gördüğünüz gibi, bu tür görevleri çözmede temelde zor bir şey yoktur. Aslında, işlem daha fazla "düz" bir figürü prizma olarak da kolaylaştırır. Şimdi aşağıdaki örneğe geçelim:

paralel yüzlü çizin 2. biz de ayrı alt tabanını çizerken, bir uçak ve doğrudan yürütmek:

İçinde yatan üç noktadan koordinatları: Öncelikle düzlem denklemini bulmak:

(İlk iki koordinat, bariz bir şekilde elde edilir ve son koordinat, dikkatlice resim bulabilirsiniz). Sonra uçağın denklemini oluşturur:

Hesaplamak:

Kılavuz vektörün koordinatlarını arıyoruz: Koordinatlarının noktanın koordinatları ile çakıştığı açık değil, değil mi? Koordinatlar nasıl? Bu, birim başına aplike ekseni boyunca yükseltilen noktanın koordinatlarıdır! . Ardından istenen açıyı arayın:

Cevap:

3. Doğru altıgen piramit koyun ve uçağı geçirin ve doğrudan geçirin.

Ancak yöntem hala koordinat Bu görevin çözümü söz, bir sorun çekemez bir uçak bile yoktur! Onun çok yönlülüğünde ve onun ana avantajı!

Uçak üç noktadan geçer :. Koordinatlarını arıyoruz:

bir) . Kendisi son iki nokta için koordinatları çıktı. Bu çözüm için altıgen piramit ile mücadeleye faydalı olacaksınız!

2) Uçağın denklemini inşa ediyoruz:

Vektörin koordinatlarını arıyoruz :. (Tekrar üçgen bir piramit ile görevi görün!)

3) Bir açı arıyoruz:

Cevap:

Gördüğünüz gibi, bu görevlerde hiçbir şey doğaüstü değildir. Sadece kökleri ile çok dikkatli olmak gerekir. Son iki göreve sadece cevap vereceğim:

Her yerde işleri çözme tekniğinin aynı şeyi nasıl yapabileceğinden emin olabilirsiniz: köşelerin koordinatlarını bulmak ve bunları belirli formüllere yerleştirmek için ana görev. Köşeleri hesaplamak için başka bir zorluk sınıfını düşünmeye bıraktık:

İki uçak arasındaki açıların hesaplanması

Algoritma çözümleri:

1. Üç puan için ilk uçağın denklemini arıyoruz:
2. Diğer üç puan için ikinci düzlemin denklemini arıyoruz:
3. Formülü kullanıyoruz:

Gördüğünüz gibi, formül önceki iki kişiye çok benzer, burada düz ve düzlem arasında köşeleri aradık. Bu yüzden bunu hatırla Çok fazla zorluk çekmeyeceksin. Hemen görevlerin analizine gidiyoruz:

1. ST-RO-OS-NO-VIL-VIL-VILTER TRE-CONSISI SONUSITİ Nerede ve Di-Hall Bo-Ko-Co-Cop'un eşittir. NAY-DI F-Co-güveç ile F-Co-Code OS-No-Viya Ödülü arasındaki açı.

2. Pra-ville-Mi-Deh-Kömür Pi-Ra-Mi-de, her kaburga, eşittir F-Co-güveç ve Co-güveç, kalem aracılığıyla Pro-Ho-FITH arasındaki köşede sinüs -Pen-di-yalancı kalem-di-yalancı, ama düz.

3. ST-RO-ABD'nin kömür kömürü ödülü, OS-NA-Via eşittir ve kenarların buketi eşittir. Benden birimin kenarında - noktaya kadar. Flat-Ko-Mi ile arasındaki açıyı bulun ve

4. Pra-Willian dört doğumlu ödülde, OS-NA-Via eşittir ve Bou - Way Ribra eşittir. Me-a noktasının kenarında, böylece NAI-DI, FLAT-KO-MI arasındaki köşeyi ve.

5. Küba'da, NAU-DI KO-SI-NUS, Flat-Co-Stey ve

Görevler Çözümleri:

1. Doğru (tabanda bir eşkenar üçgendir) bir üçgen prizma ve sorunun durumunda görünen uçaklar üzerindeki not:

İki uçağın denklemlerini bulmalıyız: Baz denklemi önemsizleştirilir: Üç nokta için uygun bir belirleyici yapabilirsiniz, derhal denklemi oluşturacağım:

Şimdi nokta denkleminin noktanın koordinatlarına sahip olduğunu bulacağız - ortanca ve üçgenin yüksekliği olduğu gibi, üçgendeki Pythagora teoreminde kolayca bulunur. Sonra Point Koordinatları Var: Bunun için başvuru noktasını bulun Dikdörtgen bir üçgen düşünün

Sonra bu koordinatları elde ediyoruz: Uçağın denklemini oluşturacağız.

Uçaklar arasındaki açıyı hesaplayın:

Cevap:

2. Çizimi yapın:

En zor şey, bunun dik olarak noktadan geçen bu kadar gizemli bir uçağın olduğunu anlamaktır. Peki, asıl şey bu mu? Asıl şey dikkat ediyor! Aslında, doğrudan diktir. Düz de diktir. Daha sonra bu iki düz çizgi boyunca geçen düzlem düz dik olması ve, bu arada, noktası üzerinden geçecek. Bu düzlem ayrıca piramitin tepesinden geçer. Sonra istenen düzlem - ve uçak zaten bize verilmiştir. Puanların koordinatlarını arıyoruz.

Noktanın koordinatı, nokta yoluyla bulacaktır. Küçük bir çizimden, noktanın koordinatlarının böyle olacağını gidermek kolaydır: Piramitin zirvesinin koordinatlarını bulmak için şimdi bulmak için şimdi ne kaldı? Hala boyunu hesaplamanız gerekir. Bu, aynı Pythagore'un teoreminin yardımı ile yapılır: önce (ilk önce küçük üçgenlerden, bazda bir kare oluşturan) kanıtlayın. Koşulladığımızdan beri:

Şimdi her şey hazır: köşelerin koordinatları:

Bir uçak denklemi yapın:

Belirleyicilerin hesaplanmasında zaten özelsiniz. Zor olmadan, alacaksınız:

Veya başka şekilde (ikisinin kökleri için her iki parça varsa)

Şimdi uçağın denklemini buluyoruz:

(Ancak, uçağın denklemini nasıl aldığımızı unutmadınız, bu eksi birinin nereden geldiğini anlamadıysanız, o zaman uçağın denkleminin tanımına geri dönün! Uçağım koordinatların başlangıcına aitti!)

Belirleyiciyi hesaplayın:

(Uçağın denkleminin, noktalardan doğrudan geçiş denklemiyle çakıştığını ve! Neden olduğunu düşünebilirsiniz!)

Şimdi açıyı hesaplıyoruz:

Ayrıca sinüs bulmalıyız:

Cevap:

3. Caverny Soru: Dikdörtgen bir prizma nedir, ne düşünüyorsunuz? Bu sadece özellikle tanınmış bir paraleldir! Hemen çizim yap! Ayrıca ayrı ayrı tasvir etmeyebilirsiniz, burada faydaları burada birazdır:

Daha önce farkettiğimiz gibi uçak, denklem şeklinde yazılır:

Şimdi bir uçak yap

Denklem, uçağın denklemidir:

Bir açı arıyoruz:

Şimdi son iki göreve cevaplar:

Eh, şimdi biz büyük çünkü biraz dinlenme zamanı ve büyük bir iş yaptın!

Koordinatlar ve vektörler. İleri düzey

mesafe hesaplama görevleri: Bu yazıda sizlerle yöntem koordinat kullanılarak çözülebilir görevlerin başka sınıfını tartışacağız. Yani, aşağıdaki durumları göz önünde bulunduracağız:

1. Krosun düz arasındaki mesafenin hesaplanması.

Bu görevleri karmaşıklıkları arttıkça emretti. Çoğu bulmak için ortaya çıkıyor noktadan uçağa olan mesafeVe en zor şey bulmak krosun düz arasındaki mesafe. Tabii ki, imkansız bir şey yok olmasına rağmen! Uzun bir kutuda ertelemeyelim ve derhal birinci görev sınıfını göz önünde bulundurmaya hemen devam edelim:

Noktadan uçağa olan mesafenin hesaplanması

Bu görevi çözmemiz için neye ihtiyacımız var?

1. Noktadaki Koordinatlar

Bu yüzden, gerekli tüm verileri alır almaz, formülü kullanırız:

Biz zaten geçen bölümde anlaşılan önceki görevleri biliniyor olmalıdır düzlemin denklemini kurmak gibi. Derhal görevlere geçelim. Şema aşağıdaki gibidir: 1, 2 - Size karar vermenize ve oldukça ayrıntılı, 3, 4 - sadece cevap, harcadığınız karar ve karşılaştırır. Başladı!

Görevler:

1. Dan Küpü. Küp kenar uzunluğu eşittir. dan kesilmiş düz-ko-st Ce-di-di Nai di- hırsız

2. Dana Pra-Vil-Naya Che-Mi-Ya-Coal-Naya Pi-Mi-Da Boe-Co-Co-RIB Stro-Ro-Os-no-via eşittir. Nay-di-that Sto-Yast, NOKTA KOŞULUK NEREDE NEREDE - SE-RE-DI-ON RIBS.

3. yılında Pra-Ville Tre-Kömür Eşit Os-No-Va-Ni-Ko-Ko-Way ile Pi-Ra-Mi-de ve bir yüz-ro-on Os-Na- eşit. Ver-Shi'den Nai Di-hırsızı, biz düz-co-st.

4. Pra-Ville dikiş kömürü ödülüne tek başına, tüm ribra eşittir. Nay-di-the Sto-Yast noktadan düz-co-st.

ÇÖZÜMLER:

Tek kenarlı bir küp çizin 1. biz mektubu göstermek bir segment ve bir uçak, segmentin orta inşa

.

İlk başta, akciğerle başlayalım: Noktanın koordinatlarını bulun. Bundan beri (segmentin ortasının koordinatlarını hatırlayın!)

Şimdi üç noktalı düzlemin denklemini derleriz

\\ [\\ Sol | (\\ BACAK (Dizi) (* (20) (C)) X & 0 & 1 \\ Y & 1 & 0 \\\\ Z & 1 & 1 \\ End (dizi)) \\ sağ | \u003d 0 \\]

Şimdi mesafeyi aramaya devam edebilirim:

2. Tüm verileri kutladığımız çizimden tekrar başlıyoruz!

Piramit için, tabanını çekmek için ayrı ayrı faydalı olacaktır.

Bir tavuk pençe olarak boyadığım gerçeği bile, bu görevi çözmeyi kolaylaştırmamızı engellemez!

Şimdi nokta koordinatlarını bulmak kolaydır

Noktanın koordinatları olarak, o zaman

2. A noktasının koordinatlarından bu yana - segmentin ortası, o zaman

Ayrıca uçağın denklemini yapmak ve basitleştirmek için uçaktaki iki noktanın koordinatlarını da buluyoruz:

\\ [\\ Sol | (\\ Sol | (\\ başlar (dizi) (* (20) (c)) x & 1 & (\\ frac (3) (2)) \\\\ Y & 0 & (\\ frac (3) (2)) \\ \\ Z & 0 & (\\ frac ((((\\ sqrt 3)) (2)) \\ ucu (dizi)) \\ sağ |) \\ sağ | \u003d 0 \\]

Puanın koordinatları olduğundan:, sonra mesafeyi hesaplarız:

Cevap (çok nadir!):

Peki, çözüldü mü? Bana öyle geliyor ki, her şeyin aynı zamanda önceki bölümde sizinle birlikte düşündüğümüz örneklerde olduğu gibi. Bu yüzden malzemenin ustalaştığını, o zaman kalan iki görevi çözmek zor olmayacağından eminim. Sadece cevap vereceğim:

Doğrudan uçağa olan mesafenin hesaplanması

Aslında, burada yeni bir şey yok. Birbirine göre düz ve uçak nasıl yerleştirilebilir? Tüm olasılıklara sahipler: çapraz veya doğrudan uçağa paralel. Ne düşünüyorsunuz, düz bir çizgiden uçağa, bu doğrudan kesiştiği uçağa mı var? Bana öyle geliyor ki mesafenin sıfır olduğu açık. İlginç olmayan dava.

İkinci durum kurnazdır: Mesafe zaten sıfırdır. Bununla birlikte, düz paralel düzlemden bu yana, her nokta bu uçağa eşdeğerdir:

Böylece:

Bu, görevimin bir öncekine delindiği anlamına gelir: Düz bir çizgide herhangi bir noktada koordinatları arıyoruz, düzlemin denklemini arıyoruz, noktadan uçağa olan mesafeyi hesaplıyoruz. Aslında, sınavdaki bu görevler son derece nadirdir. Sadece bir görev bulmayı başardım ve içindeki veriler koordinat yönteminin kendisine çok uygulanmadı!

Şimdi başka birine dönüyoruz, çok daha önemli bir görev sınıfı:

Mesafe noktasının doğrudan hesaplanması

Neye ihtiyacımız var?

1. Mesafeyi aradığımız noktanın koordinatları:

2. Hatta yatan herhangi bir noktayı koordinatları

3. Doğrudan Vektörler Doğrudan Koordinatlar

Hangi formül?

Bu fraksiyonun paydası sizin için ne ifade ediyor ve böylece açık olmalı: Rehber vektörünün düz uzunluğu. İşte çok kurnaz bir rakam! İfade, vektörlerin vektör ürününün modülü (uzunluğu) ve vektör çalışmalarını nasıl hesaplayacağımız, işin önceki bölümünde incelendik. Bilginizi güncelleyin, şimdi bizim için çok faydalı olacaklar!

Böylece, problem çözme algoritması aşağıdakiler olacaktır:

1. Biz mesafeye arıyoruz hangi noktanın koordinatlarının arıyoruz:

2. Mesafeyi aradığımız hattın herhangi bir noktasının koordinatlarını arıyoruz:

3. Vektör inşa

4. Çizgi kılavuz vektörünü oluşturun

5. Vektör sanatını hesaplayın

6. Elde edilen vektörün uzunluğunu arıyoruz:

7. Mesafeyi hesaplayın:

Çok fazla işimiz var ve örnekler oldukça karmaşık olacak! Yani şimdi tüm dikkat!

1. dana pra-vil-naya tre-kömür-naya pi-ra-mi-evet ile ver-shih. OS-NO-VIYA PI-RA-MI-DYA ON-RA-RA-MI-DYA eşittir, so-so-yani eşittir. Düz se D-di-ko-ko-kaburga, Nai di- hırsız burada noktaları ve - yeniden di kaburga ve ko-dan-mesleki-aşağı.

2. kaburga uzunlukları ve direkt m kömür-büt-Goa Parale-le-le-pi-Evet ko-damar-den eşittir - Ver-Shi-re den de ancak NAI-di-hırsız -Direct

3. Pra-ville dikiş kömür ödül başına, her kaburga düz noktaya NAI-di-hırsız Rota eşittir

ÇÖZÜMLER:

1. Tüm verileri işaretleyen düzgün bir çizim yapın:

Sizinle çok fazla işimiz var! İlk önce arayacağımız kelimeleri ve hangi sırayla tanımladığımızı tarif ederdim:

1. Puanın koordinatları ve

2. Noktadaki Koordinatlar

3. Puanların koordinatları ve

4. Vektörlerin koordinatları ve

5. Onların vektör sanatları

6. Vektör uzunluğu

7. Vektör uzunluğu uzunluğu

8. -Otan uzaklık

Çok fazla işimiz var! Onun için kabul edilir, kolları sıkıyoruz!

1. Piramit yüksekliğinin koordinatlarını bulmak için, uygulamasının noktasının koordinatlarını sıfıra eşit olarak bilmemiz gerekir ve koordinatın, yüksekliğinden bu yana segmentin uzunluğuna eşittir. Eşkenar üçgen, daha sonra üstten sayım, dolayısıyla ilişkiye ayrılır. Son olarak, koordinatlar aldılar:

Noktanın koordinatları

2. - orta kesim

3. - orta segment

Orta derecede

4.Kopinatlar

Vektörin koordinatları

5. Vektör sanatını hesaplayın:

6. Vektörin uzunluğu: En kolay yolu, segmentin üçgenin orta çizgisi olduğu, yani tabanın yarısına eşit olduğu anlamına gelir. Böylece.

7. Vektör işinin uzunluğunu düşünüyoruz:

8. Sonunda, mesafeyi buluruz:

UV, iyi! Dürüst olmak gerekirse, söyleyeceğim: Bu sorunun geleneksel yöntemlerle (inşaat yoluyla) çözümü çok daha hızlı olacaktır. Ama burada hepimiz bitmiş algoritmaya indirdim! Bu yüzden algoritmanın senin için açık olduğunu düşünüyorum? Bu nedenle, kalan iki görevi kendiniz çözmeni isteyeceğim. Cevapları karşılaştır?

Yine tekrar ediyorum: Bu görevler yapılardan çözmek için daha kolay (daha hızlı) ve koordinat yöntemine başvurmamak. Sadece size bir şey tutmanıza izin veren evrensel bir yöntem göstermek için böyle bir çözümü gösterdim. "

Son olarak, son görev sınıfını göz önünde bulundurun:

Krosun düz arasındaki mesafenin hesaplanması

Burada, görevleri çözmek için algoritma öncekine benzer olacaktır. Neyimiz var:

3. Herhangi bir vektör bağlantı noktası birinci ve ikinci düz:

Düz arasındaki mesafeyi nasıl arıyoruz?

Formül aşağıdaki gibidir:

Numarator, karışık bir ürünün bir modülüdür (önceki bölümde uygulandık) ve payda önceki formül (doğrudan doğrudan vektörlerin vektör ürününün modülü, aradığımız mesafeden) olduğu gibidir. .

Bunu sana hatırlatacağım

sonra mesafenin formülü formda yeniden yazılabilir:

Belirleyiciyi paylaşmak için tek belirleyici! Her ne kadar dürüst olmak gerekirse, burada hiç şaka yapmıyorum! Bu formül, aslında, çok hantal ve yeterince karmaşık hesaplamalara yol açar. Yerinizde, sadece en aşırı durumda başvururdum!

Yukarıda belirtilen yöntemi kullanarak birkaç görevi çözmeye çalışalım:

1. TRE-VILLE, TRE-VILLE ÖDÜLÜ, tüm RIBR KO-ROY eşittir, NAI DI-DROUS.

2. Dana-Vil-Naya Tre-Coal-Naya Ödül-MA Tüm RIB OS-Via-Way, SE-İNSANSA, PRO-HO-Dedesi'ne, EDGE ve SE-RE- DI Java-Lhaa-Xia Kvad-Ra-Tom'un kaburgalarıdır. Nay-di-thes rostozhone arasında riyolar ve

İlk önce çözdüm ve üzerine güveniyordum, ikinciye karar veriyorsun!

1. Bir prizma çiziyorum ve düz olarak işaret ediyorum ve

C noktasının koordinatları: o zaman

Noktanın koordinatları

Vektörin koordinatları

Noktanın koordinatları

Vektörin koordinatları

Vektörin koordinatları

\\ [\\ sol ((B, \\ outrightarrow (a (a_1)) \\ outrightarrow (B (B_1))) \\ sağ) \u003d \\ Sol | (\\ BACAK (Dizi) (* (20) (L)) (\\ BACE (Dizi) (* (* (20) (c)) 0 & 1 & 0 ucu (dizi) \\\\\\ (\\ BACAK (dizi) (* (20) (c)) 0 & 0 & 1 \\ ucu (dizi)) \\\\ (\\ BACE (dizi) (* (20) (c)) (\\ frac ((\\ sqrt 3)) (2)) ve (- \\ frac (1) (2)) & 1 \\ end (dizi)) \\ end (dizi)) \\ sağ | \u003d \\ Frac ((\\ sqrt 3)) (2) \\]

Vektör ürünler arasında vektör ürünü ve

\\ [\\ Outrightarrow (A (A_1)) \\ CDOT \\ outrightarrow (B (C_1)) \u003d \\ Sol | \\ BAŞLATA (Dizi) (L) \\ BAŞLATI (dizi) (* (20) (c)) (\\ outrightarrow i) & (\\ outrightarrow j) & (\\ outrightarrow k) \\ ucu (dizi) \\\\\\ başlamak (dizi) ) (* (20) (c)) 0 & 0 & 1 \\ ucu (dizi) \\\\\\ Başlayın (dizi) (* (20) (c)) (\\ frac ((\\ sqrt 3)) (2)) & (- \\ frac (1) (2)) & 1 \\ end (dizi) \\ end (dizi) \\ sağ | - \\ frac ((\\ sqrt 3)) (2) \\ overrightarrow k + \\ frac (1) (2) \\ outrightarrow i \\]

Şimdi bir uzunluk olduğunu düşünüyoruz:

Cevap:

Şimdi ikinci görevi doğru bir şekilde yerine getirmeye çalışın. Cevap şu olacak :.

Koordinatlar ve vektörler. Kısa Açıklama ve Temel Formüller

Stok Fotoğraf - Yönlü kesim. - Vektörin başlangıcı, - İçerik Vektör.
Vektör gösterilir veya.

Mutlak değerstok Fotoğraf - Vektör tasvir eden uzunluğu. Olarak adlandırılır.

Vektörin koordinatları:

,
nerede - vektörün uçları \\ DisplayStyle a.

Vektörlerin toplamı :.

Vektörleri Yapma:

Vektörlerin Skaler Ürünü:

Vektörlerin skaler ürünü, aralarındaki açının kosinüsündeki mutlak değerlerinin ürününe eşittir:

Sizce öğrenci olun,

Matematikte Oge veya Ege için hazırlanın,

Ve ayrıca size kısıtlamalar olmadan Sizce ders kitabına erişin ...

Video eğitimi "Coğrafi enlem ve coğrafi boylam. Coğrafi koordinatlar "Coğrafi enlem ve coğrafi boylam hakkında bir fikir edinmenize yardımcı olacaktır. Öğretmen coğrafi koordinatları nasıl düzgün bir şekilde belirleyeceğini söyleyecektir.

Coğrafi enlem- ARC'nin ekvatordan verilen bir noktaya derecelerdeki uzunluğu.

Nesnenin enlemini belirlemek için, bu nesnenin bulunduğu paralel bulmanız gerekir.

Örneğin, Moskova'nın enlemi 55 derece ve 45 dakikalık kuzey enlemdir, aşağıdaki gibi yazılmıştır: Moskova 55 ° 45 "S.SH.; New York Latitude - 40 ° 43" S.SH.; Sidney - 33 ° 52 "YU.SH.

Coğrafi boylam meridyenler tarafından belirlenir. Boylam batılı (0 meridyenden batıdan 180 meridyen) ve Doğu (0 meridyen doğudan 180 meridyen) olabilir. Uzunlamaların değeri derece ve dakikalar içinde ölçülür. Coğrafi boylam, 0 ila 180 dereceden bir değere sahip olabilir.

Coğrafi boylam- Equator ark, ilk meridyenden (0 derece), belirtilen noktanın meridyenine derecelerde uzunluğu.

Greenwich Meridian ilk Meridian (0 derece) olarak kabul edilir.

İncir. 2. Boylamın tanımı ()

Boylamı belirlemek için, belirtilen nesnenin bulunduğu Meridian'ı bulmanız gerekir.

Örneğin, Moskova'nın boylamı - 37 derece ve 37 dakikalık doğu boylam, bu şekilde yazılmıştır: 37 ° 37 "VD; Mexico City'nin boylamı - 99 ° 08" ZD

İncir. 3. Coğrafi enlem ve coğrafi boylam

Nesneyi Dünya'nın yüzeyinde doğru bir şekilde bulmak için, coğrafi enlemini ve coğrafi boylamını bilmek gerekir.

Coğrafi Koordinatlar- Enlemler ve boylam yardımı ile yer yüzeyindeki noktanın konumunu belirleyen değerler.

Örneğin, Moskova aşağıdaki coğrafi koordinatlara sahiptir: 55 ° 45 "S.SH. ve 37 ° 37" V.D. Pekin şehri aşağıdaki koordinatlara sahiptir: 39 ° 56 'S.SH. 116 ° 24 'VD İlk olarak, enlemin değeri kaydedilir.

Bazen, önceden belirtilen koordinatlarda bir nesneyi bulmak gerekir, çünkü bunun için önce hemisferlerin bu nesne olduğunu varsaymalısınız.

Ödev

12, 13. paragraflar.

1. Coğrafi enlem ve boylam nedir?

Bibliyografi

Temel

1. Coğrafya'nın ilk kursu: Çalışmalar. 6 cl için. Genel Eğitim. kurumlar / vb. Gerasimova, N.P. Nezlukov. - 10. ed., Klişe. - m.: Bırak, 2010. - 176 s.

2. Coğrafya. 6 CL.: Atlas. - 3. ed., Basmakalıp. - m.: Bırak, Dick, 2011. - 32 s.

3. Coğrafya. 6 CL.: Atlas. - 4. ed., Klişe. - m.: Bırak, Dick, 2013. - 32 s.

4. Coğrafya. 6 cl.: Devam kartlar. - m.: Dick, Drop, 2012. - 16 p.

Ansiklopediler, sözlükler, dizin ve istatistiksel koleksiyonlar

1. Coğrafya. Modern resimli ansiklopedi / A.P. Gorkin. - M.: Rosman-Press, 2006. - 624 s.

Gia ve Ege için hazırlık edebiyatı

1. Coğrafya: İlk kurs. Testler. Çalışmalar. 6 cl'lik öğrenciler için el kitabı. - m.: İnsani. ed. Merkez Vlados, 2011. - 144 s.

2. Testler. Coğrafya. 6-10 CL.: Eğitim ve Metodik El Kitabı / A.A. Letlyagin. - m.: Acentelik "Ajansı" KRP "Olymp": "Astrel", "AST", 2001. - 284 s.

İnternetteki malzemeler

1. Federal Pedagojik Ölçümler Enstitüsü ().

2. Rus coğrafi toplum ().