Gizliliğinize uygunluk bizim için önemlidir. Bu nedenle, bilgilerinizi nasıl kullandığımızı ve sakladığımızı açıklayan bir gizlilik politikası geliştirdik. Lütfen Gizlilik Politikamızı okuyun ve herhangi bir sorunuz varsa bize bildirin.

Kişisel bilgilerin toplanması ve kullanımı

Kişisel bilgiler altında, belirli bir kişiyi tanımlamak veya onunla iletişim kurmak için kullanılabilecek verilere tabidir.

Kişisel bilgilerinizi bizimle bağlantı kurduğunuzda istediğiniz zaman sunmanız istenebilir.

Aşağıda, toplayabileceğimiz kişisel bilgiler türlerinin bazı örnekleri ve bu bilgileri nasıl kullanabileceğimizi.

Topladığımız Kişisel Bilgiler:

• Sitede bir uygulama bıraktığınızda, adınız, telefon numaranız, e-posta adresiniz vb. Dahil olmak üzere çeşitli bilgiler toplayabiliriz.

Kişisel bilgilerinizi kullanırken:

• Kişisel bilgiler topladık, sizinle iletişim kurmamızı ve benzersiz teklifler, promosyonlar ve diğer etkinlikler ve en yakın etkinlikler hakkında rapor etmemizi sağlar.
• Zaman zaman, kişisel bilgilerinizi önemli bildirimler ve mesajlar göndermek için kullanabiliriz.
• Ayrıca, hizmetlerimizin hizmetlerini geliştirmek ve hizmetlerimiz için önerileri sağlamak için denetim, veri analizi ve çeşitli çalışmalar gibi içsel amaçlar için kişiselleştirilmiş bilgileri kullanabiliriz.
• Ödüller, rekabet veya benzeri uyarıcı olayı katılıyorsanız, bu programları yönetmek için sağladığınız bilgileri kullanabiliriz.

Üçüncü Partilere Bilgi Açıklaması

Sizden alınan bilgileri üçüncü şahıslara açıklamıyoruz.

İstisnalar:

• Gerektiğinde - Yasaya, adli prosedüre, duruşmada ve / veya kamu sorgularına ve devlet kuruluşlarından devlet kuruluşlarının talepleri temelinde - kişisel bilgilerinizi ortaya çıkarmak için. Bu tür açıklamanın gerekli olup olmadığını, yasa ve siparişin korunması veya diğer sosyal açıdan önemli durumları korumak için gerekli veya uygun olduğunu tanımlarsak, sizin hakkınızdaki bilgileri de ifşa edebiliriz.
• Yeniden düzenleme, birleşme veya satış durumunda, bir halefi olan üçüncü tarafa karşılık gelen kişisel bilgileri iletebiliriz.

Kişisel Bilgilerin Korunması

İdari, teknik ve fiziksel dahil - kişisel bilgilerinizi kayıp, hırsızlık ve ahlaksız kullanımdan ve yetkisiz erişim, açıklama, değişiklik ve yıkımdan korumak için önlemler alıyoruz.

Şirket düzeyinde gizliliğinize uygunluk

Kişisel bilgilerinizin güvende olduğundan emin olmak için, çalışanlarımıza gizlilik ve güvenlik normlarını getiriyoruz ve gizlilik önlemlerinin yürütülmesini kesinlikle takip ediyoruz.

Noktadan uçağa olan mesafeyi araştırmak, analitik geometrinin çeşitli görevlerini çözerken meydana gelen sık görülen sık görülen bir görevdir, örneğin, bu soruna, iki çapraz yaşanmış, düz veya düz ve paralel düzlem arasındaki mesafeyi azaltabilirsiniz.

$ Β $ ve $ M_0 $ 'ı M_0 $' ı Koordinatlarla (X_0; Y_0; Z_0) $ 'a ait değil, $ β $ Uçağına ait değil.

Tanım 1.

Nokta ile uçak arasındaki en kısa mesafe dik olacak, $ M_0 $ işaretinden uçakla $ β $ 'dan indirdi.

Şekil 1. Noktadan, uçağa olan mesafe. Author24 - Öğrenci İnternet Değişimi

Aşağıdakiler, noktadan uçağa olan mesafeyi koordinat yöntemiyle buldukları kabul edilir.

Koordinat yönteminin formülünü, noktadan uçakla uzayda aradığı mesafeyi araştırmak için gösterir.

$ M_0 $ 'dan, $ β $ uçakla kesişen $ β $ uçakla kesişen $ (x_1; y_1; z_1) $, Rehber vektörünün normal vektörünün normal vektörü olan düz bir çizgide yatıyor. Bu durumda, birimin uzunluğu $ N $ N $ birine eşittir. Buna göre, $ β $ 'dan $ M_0 noktasına kadar bu mesafe:

$ ρ \u003d | \\ vec (n) \\ CDOT \\ VEC (M_1M_0) | \\ sol (1 \\ sağ) $, burada $ \\ vec (m_1m_0) $ normal bir uçak vektör $ β $ ve $ \\ vec (n) $ - Düşünce altındaki uçağın tek normal vektörü.

Uçağın denkleminin toplam formda belirtildiği durumlarda, $ balta + tarafından + cz + d \u003d 0 $ tarafından belirtilirse, normal düzlem vektörünün koordinatları, Denklem'in katsayılarıdır \\ (a; b; c \\) $ ve bu durumda tek normal vektör, aşağıdaki denklem ile hesaplanan koordinatlara sahiptir:

$ \\ vec (n) \u003d \\ frac (\\ (a; b; c ^ 2 + c ^ 2)) \\ Sol (2 \\ sağ) $.

Şimdi normal vektörün koordinatlarını $ \\ VEC (M_1M_0) $ bulabilirsiniz:

$ \\ Vec (m_0m_1) \u003d \\ (x_0 - x_1; y_0-y_1; z_0-z_1 \\) \\ sol (3 \\ sağ) $.

Ayrıca $ D $ uçakta yatan noktanın koordinatlarını kullanarak $ D $ katsayısını ifade eder:

$ D \u003d AX_1 + BY_1 + CZ_1 $

Tek normal vektörün eşitlikten koordinatları $ (2) $ (2) $, uçak denklemi ile ikame edilebilir $ β $, sonra:

$ ρ \u003d \\ frac (| a (x_0 -x_1) + b (y_0-y_1) + c (z_0-z_1) |) (\\ sqrt (a ^ 2 + b ^ 2 + c ^ 2)) \u003d \\ frac ( | AX_0 + BY_0 + CZ_0- (AX_1 + BY_1 + CZ_1) |) (\\ SQRT (A ^ 2 + B ^ 2 + C ^ 2)) \u003d \\ Frac (AX_0 + BY_0 + CZ_0 + D) (\\ SQRT (A ^ 2 + B ^ 2 + C ^ 2)) \\ Sol (4 \\ sağ) $

Eşitlik $ (4) $, noktadan uçakla uzayda olan mesafeyi bulmak için formüldür.

M_0 $ noktasından uçağa olan mesafeyi bulmak için genel algoritma

1. Düzlemin denklemi genel olarak belirtilmemişse, bir başlangıç \u200b\u200biçin ortak olana getirmek gerekir.
2. Bundan sonra, bu uçağın genel düzlem denkleminin normal vektörünü bir M_0 $ ile ve belirtilen uçağa ait bir nokta ile ifade etmek gerekir; bunun için (3) $ (3) $ 'lık eşitlik kullanmanız gerekir.
3. Bir sonraki adım, uçağın normal vektörünün birimin koordinatlarını (2) $ formülüyle aramaktır.
4. Son olarak, noktadan uçağa olan mesafeyi araştırmak mümkündür, bu, $ \\ vec (n) $ ve $ \\ vec (M_1M_0) $ vektörlerinin skaler ürününü hesaplayarak gerçekleştirilir.

Bu makale, noktadan uçağa olan mesafeyi belirlemeyi anlatır. Üç boyutlu boşluğun belirli bir noktasından uzaklığa izin veren koordinat yöntemini analiz edeceğiz. Konsolidasyon için, çeşitli görevlerin örneklerini düşünün.

Noktadan uçağa olan mesafe, noktadan noktaya, bunlardan birinin belirtildiği noktaya kadar bilinen bir mesafe vasıtasıyla bulunur, diğeri de belirli bir düzlemde bir çıkıntıdır.

Bir Puntion M1, bir düzlem χ olan boşlukta ayarlandığında, dik düzlem noktası boyunca yapılabilir. H 1, kavşaklarının ortak bir noktasıdır. Buradan, M1 H1 segmentinin, M1 noktasından düzlemden çıkan bir dikey olduğunu, burada H'nin, H1 noktasının dikin tabanı olduğu bir dikeydir.

Tanım 1.

Belirli bir noktadan belirli bir noktadan belirli bir noktadan gerçekleştirilen, belirli bir noktadan olan mesafeyi ararlar.

Tanım, farklı formülasyonlarda kaydedilebilir.

Tanım 2.

Noktadan uçağa olan mesafe Belirli bir noktadan belirli bir uçağa harcanan dikin uzunluğunu çağırırlar.

M1 noktasından uçağa olan mesafe χ aşağıdaki gibi belirlenir: M1 noktasından uçağa olan mesafe χ, uçağın herhangi bir noktasında belirtilen noktadan en küçüğü olacaktır. H2 nokta düzlemde bulunursa ve H2 noktasına eşit değilse, m2h1 h 2'nin dikdörtgen bir üçgeni elde ediyoruz. bir katat m 2 h1, m 2 saat 2'nin olduğu dikdörtgendir. - hipotenüs. Öyleyse, bu, m 1 h 1'i takip eder.< M 1 H 2 . Тогда отрезок М 2 H 1 m1 noktasından düzlemden çıkan eğik olarak kabul edilir. Verilen bir noktadan uçağa doğru yürütülen, daha az eğimlidir, bu noktadan belirtilen uçağa doğru yapılır. Bu durumu aşağıdaki şekilde düşünün.

Noktadan Uçağa Uzaklık - Teori, Örnekler, Çözümler

Çözümleri, noktadan uçağa olan mesafeyi içermesi gereken bir dizi geometrik görev vardır. Bunu tanımlamak için yöntemler farklı olabilir. İzin için, Pythagora'nın teoremi veya üçgenlerin benzerliği kullanılır. Durumla, duruma göre, üç boyutlu boşluğun dikdörtgen koordinat sisteminde belirtilen noktadan uçağa olan mesafeyi hesaplamak gerekir, koordinat yöntemini çözün. Bu ürün bu yöntemi dikkate alır.

Sorun sorunu ile, Koordinatlar M1 (x 1, Y1, Z 1) ile üç boyutlu boşluk noktasının düzleme verildiğine, M1'den gelen mesafeyi belirlemek gerekir. Uçak χ. Çözmenin birkaç yolunu çözmek için.

İlk yöntem

Bu yöntem, M1 noktasından düzlemden (M1) noktasından düzlemin tabanı olan H1'in koordinatlarını kullanarak noktadan uçtan uzaklığa dayanmaktadır. Daha sonra, M1 ile H 1 arasındaki mesafeyi hesaplamak gerekir.

Sorunu çözmek için, belirtilen düzlemin normal denklemi ikinci yöntemde kullanılır.

İkinci yol

Durumuna göre, H 1'sinin, M1 noktasından düzlemden aşağıya indirilen dikin temelidir. Sonra koordinatları belirleriz (x 2, y2, z2) puan H 1. M1'den düzlemden istenen mesafe χ, M1 h1 \u003d (x 2 - x 1) 2 + (y2 - z 1) 2 + (Z 2 - z 1) 2, burada M formülüne göre bulunur. 1 (x 1, y 1, z 1) ve H1 (x 2, y2, z2). Çözmek için H 1 noktasının koordinatlarını bilmek gerekir.

H 1'siyiz, düzlemin χ'sinin Direct A ile kesişme noktasıdır, bu da uçağa dik olan M1 noktasından geçer. Doğrudan geçişinin belirtilen noktadan belirtilen düzleme dik olarak derlenmesini derlemenin gerekli olduğunu takip eder. Daha sonra H 1 noktasının koordinatlarını belirleyebileceğimizdir. Doğrudan ve düzlemin kesiştiği koordinatlarını hesaplamak gerekir.

Koordinatlar M1 (X 1, Y 1, Z 1) ile uçağa olan mesafeyi bulmak için algoritma χ:

Tanım 3.

• doğrudan a iletişini M1 noktasından ve aynı zamanda
• uçağa dik χ;
• koordinatları bulun ve hesaplayın (x 2, y2, z2) noktaları H1, işaretlerdir.
• kavşak doğrudan A düzlemi ile χ;
• m1 ila χ formülünü kullanarak M1 ila χ arasındaki mesafeyi hesaplayın (x 2 - x 1) 2 + (Y2 - Y 1) 2 + Z 2 - Z 1 2.

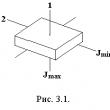
Üçüncü yol

Belirli bir dikdörtgen koordinat sisteminde, Z'deki X'in koordinatları bir düzleme sahiptir, daha sonra formun düzleminin normal denklemini elde ediyoruz COS α · x + cos β · y + cos γ · z - p \u003d 0. Buradan, m1 (x 1, y1, z 1) bir nokta m1 (x 1, y1, z 1) ile yapılan mesafe χ Formül M1 H 1 \u003d COS α · x + cos β · Y + COS Γ · z - s. Bu formül geçerlidir, çünkü bu teorem sayesinde kurulur.

Teorem

M (X 1, Y1, Z 1), formun normal bir denklemine sahip olan üç boyutlu bir alanda belirtilmişse COS α · x + cos β · y + cos γ · z - p \u003d 0 , ardından noktadan m1 h 1 düzlemine kadar olan mesafenin hesaplanması, M1 H1 formülünden yapılmıştır \u003d COS α · x + cos β · y + cos α · z - p, x \u003d x 1, y \u003d y 1, z \u003d z 1.

Kanıt

Teoremin kanıtı, noktadan doğrudan olan mesafeyi bulmak için azaltılır. Buradan, M1'den uçağa olan mesafenin χ'sinin, yarıçapı vektörünün sayısal projeksiyonundaki farkın modülü olup olmadığını, orijinden uçağa olan mesafe χ. Sonra m 1 h1 \u003d n p n → o m → - p ifadesini elde ederiz. Uçağın normal vektörü χ n → \u003d cos α, cos β, cos γ ve uzunluğu birine eşittir, NPN → OM → - vektörün OM'nin sayısal projeksiyonu → \u003d (x 1, Y 1 , Z 1) Vektör N → tarafından belirlenen yönde.

Skaler vektörleri hesaplamak için formülü uygulayın. Sonra n →, OM → \u003d \u003d n → · NPN → OM → \u003d 1 · NPN → OM → \u003d NPN → OM →, n → \u003d cos α, cos β, cos γ'den · Z ve OM → \u003d (x 1, y 1, z 1). Kayıtın koordinat formu, N →, OM → \u003d COS α · x 1 + COS β · Y 1 + COS Γ · Z 1, ardından M 1 H 1 \u003d NPN → OM → P \u003d COS α · x 1 + cos β · y 1 + cos γ · z 1 - s. Teoremi kanıtlandı.

Buradan, M 1 noktasından (x 1, y1, z 1) noktasından uçağa olan mesafenin, COS α · x + cos β · y'nin normal denkleminin sol kısmındaki ikame kullanılarak hesaplandığını elde ediyoruz. + cos γ · z - p \u003d 0 x, y, z koordinatları x 1, Y 1 ve z 1. M1 noktasına ait, elde edilen değerin mutlak değerini alarak.

Koordinatlarla noktadan olan mesafeyi belirtilen uçağa bulma örneklerini düşünün.

Örnek 1.

M (5, - 3, 10) koordinatları 2 x - y + 5 z - 3 \u003d 0 düzlemine olan koordinatlarla olan mesafeyi hesaplayın.

Karar

Sorunu iki şekilde çözeceğiz.

İlk yöntem, doğrudan a kılavuz vektörünün hesaplanmasıyla başlayacaktır. Durumuna göre, verilen denklem 2 x - y + 5 z - 3 \u003d 0, genel formun düzleminin denklemidir ve n → \u003d (2, - 1, 5) belirtilenlerin normal bir vektörüdür. uçak. Belirtilen uçağa dik olan kılavuz vektörü doğrudan A olarak kullanılır. Kanonik denklem, 2, - 1, 5 koordinatları olan bir kılavuz vektör ile M1 (5, - 3, 10) geçerek uzayda kaydedilmelidir.

Denklem x - 5 2 \u003d y - (- 3) - 1 \u003d z - 10 5 ⇔ x - 52 \u003d y + 3 - 1 \u003d z - 105 formunu alacak.

Kavşak noktalarını tanımlamanız gerekir. Bunu yapmak için, denklemleri nazikçe, kanonikten kesişen iki düz çizginin denklemlerine geçiş için denklemleri sisteme birleştirin. Bu nokta 1'den çıkar. Bunu alıyoruz

x - 5 2 \u003d Y + 3 - 1 \u003d Z - 10 5 ⇔ - 1 · (x - 5) \u003d 2 · (Y + 3) 5 · (x - 5) \u003d 2 · (z - 10) 5 · ( Y + 3) \u003d - 1 · (Z - 10) ⇔ ⇔ x + 2 Y + 1 \u003d 0 5 x - 2 Z - 5 \u003d 0 5 Y + Z + 5 \u003d 0 ⇔ X + 2 Y + 1 \u003d 0 5 x - 2 z - 5 \u003d 0

Sistemi çözmek için gerekli olandan sonra

x + 2 Y + 1 \u003d 0 5 x - 2 Z - 5 \u003d 0 2 x - Y + 5 Z - 3 \u003d 0 ⇔ x + 2 Y \u003d 1 5 x - 2 Z \u003d 5 2 x - Y + 5 Z \u003d 3.

Gauss'ta sistemin kuralına dönelim:

1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z \u003d 0 6 \u003d 0, y \u003d - 1 10 · 10 + 2 · z \u003d - 1, x \u003d - 1 - 2 · y \u003d 1

Bunu H 1 (1, - 1, 0) elde ediyoruz.

Belirtilen noktadan uçağa kadar mesafe hesaplamaları üretiyoruz. M1 noktasını (5, - 3, 10) ve H1 (1, - 1, 0) alıp alın

M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30

Çözeltinin ikinci çözeltisi, belirtilen denklemi 2 x - y + 5 z - 3 \u003d 0'a normal formlara getirmeye başlamaktır. Normalleştirici çarpanı belirliyoruz ve 1 2 2 + (- 1) 2 + 5 2 \u003d 1 30 elde ediyoruz. Bu nedenle, düzlemin denklemi 2 30 · x - 1 30 · y + 5 30 · z - 3 30 \u003d 0. Denklemin sol kısmının hesaplanması, X \u003d 5, Y \u003d - 3, Z \u003d 10'un ikame edilmesiyle yapılır ve M1 (5, - 3, 10) ila 2 x arasındaki mesafeyi almanız gerekir - Y + 5 Z - 3 \u003d 0 modül ile. İfade edelim:

M 1 h 1 \u003d 2 30 · 5 - 1 30 · - 3 + 5 30 · 10 - 3 30 \u003d 60 30 \u003d 2 30

Cevap: 2 30.

Düzlem χ, düzlemi ayarlama yöntemlerinin yöntemlerinden birinde ayarlandığında, χ düzleminin denklemini elde etmeye ve istenen mesafeyi herhangi bir yöntem kullanarak hesaplamak için gereklidir.

Örnek 2.

Üç boyutlu alanda, noktalar, M1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1) koordinatlar ile ayarlanır. M1'den uçağın A'yı C'deki A'yı hesaplayın.

Karar

Başlamak için, üç noktadan geçen düzlemin denklemini, M1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1) koordinatları ile kaydetmek gerekir. C (4, 0, bir).

x - 0 Y - 2 Z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 \u003d 0 ⇔ XY - 2 Z - 1 2 4 0 4 - 2 - 2 \u003d 0 ⇔ ⇔ - 8 x + 4 Y - 20 z + 12 \u003d 0 ⇔ 2 x - Y + 5 Z - 3 \u003d 0

Buradan, görevin bir öncekine benzer bir çözüme sahip olduğunu takip eder. Bu, M1 noktasından C'deki bir uçağa olan mesafenin 2 30 değerine sahip olduğu anlamına gelir.

Cevap: 2 30.

Düzlemdeki belirli bir noktadan veya paralel oldukları düzlemden uzaklığı bulmak, daha uygun, daha uygun, formül M1 h1 \u003d cos α · x 1 + cos β · y 1 + cos Γ · z 1 - p . Buradan, uçakların normal denklemlerinin çeşitli eylemlerde elde edildiğini elde ediyoruz.

Örnek 3.

Belirtilen noktadan, M1 (- 3, 2, - 7) koordinatlarıyla, X'teki X'in koordinat düzlemine ve Denklem 2 - 5 \u003d 0 tarafından verilen düzlemin bulunduğu mesafeyi bulun.

Karar

Z'deki koordinat düzlemi, X \u003d 0 türlerinin denklemine karşılık gelir. Z düzlemi için, normaldir. Bu nedenle, X \u003d - 3 ekspresyon değerinin solunda ikame etmek gerekir ve mesafe değerinin modülünü, M1 (- 3, 2, - 7) düzleme koordinatları ile noktadan gelin. 3 \u003d 3'e eşit bir değer elde ediyoruz.

Dönüşümden sonra, düzlemin normal denklemi 2 Y - 5 \u003d 0 Y - 5 2 \u003d 0 izlenecektir. Ardından, istenen mesafeyi, M1 (- 3, 2, - 7) düzlemine 2 y - 5 \u003d 0 koordinatlarıyla birlikte bulabilirsiniz. Değiştirme ve hesaplama, 2 - 5 2 \u003d 5 2 - 2 elde ediyoruz.

Cevap: Z 1'deki M1 (- 3, 2, - 7) 'den istenen mesafe, 3 değerine sahiptir ve 2 ila 5 \u003d 0, 5 2 - 2'dir.

Metinde bir hata görürseniz, lütfen seçin ve Ctrl + Enter tuşuna basın.

Uzayda bazı düzlemler π ve keyfi bir nokta m 0 olarak düşünün. Bir uçak için seçin birim normal vektör N S. başlangıç Bazı noktada m 1 ∈ π ve p (m 0, π), M 0 noktasından düzleme kadar bir mesafe olsun. Sonra (Şek. 5.5)

p (m 0, π) \u003d | Pr n m 1 m 0 | \u003d | NM 1 m 0 |, (5.8)

nO | N | \u003d 1.

Uçak π olarak ayarlanmışsa ortak denklemi ile dikdörtgen koordinat sistemi AX + by + CZ + D \u003d 0, daha sonra normal vektör, koordinatlar (a; b; c) olan vektördür (A; B; C) ve tek bir normal vektör olarak seçebilirsiniz

(X 0; y 0; z 0) ve (x 1; y 1; z 1) M 0 ve m 1 noktalarının koordinatları. Sonra Eşlik Baltası 1 + ile 1 + CZ 1 + D \u003d 0 ile yapılır, çünkü M1 noktası düzleme aittir ve vektör M1 m 0: m 1 m 0 \u003d (x 0-x 1) ; Y 0 -Y 1; Z 0 -Z 1). yazı skaler ürün NM 1 m 0 koordinat formunda ve dönüştürme (5.8), biz

balta 1 + 1 + Cz 1 \u003d - D.N. normalleştirici bir çarpana bölünmüş, karşılık gelen normal vektörün uzunluğuna eşittir.