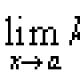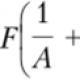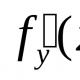The amount of motion of the system, as a vector quantity, is determined by formulas (4.12) and (4.13).

Theorem. The derivative of the momentum of the system with respect to time is equal to the geometric sum of all external forces acting on it.

In the projections of the Cartesian axes, we obtain scalar equations.

You can write a vector

(4.28)

and scalar equations

Which express the theorem about the change in the momentum of the system in integral form: the change in the momentum of the system over a certain period of time is equal to the sum of impulses over the same period of time. When solving problems, equations (4.27) are often used

The law of conservation of momentum

The theorem on the change in the angular momentum

The theorem on the change in the angular momentum of a point relative to the center: the time derivative of the angular momentum of a point relative to a fixed center is equal to the vector moment acting on the point of force relative to the same center.

or (4.30)

Comparing (4.23) and (4.30), we see that the moments of the vectors and are related by the same dependence as the vectors and themselves (Fig. 4.1). If we project the equality onto the axis passing through the center O, then we get

(4.31)

This equality expresses the theorem of the angular momentum of a point about an axis.

(4.32)

If we project expression (4.32) on the axis passing through the center O, then we obtain an equality characterizing the theorem on the change in the angular momentum relative to the axis.

(4.33)

Substituting (4.10) into equality (4.33), we can write down the differential equation of a rotating rigid body (wheels, axles, shafts, rotors, etc.) in three forms.

(4.34)

(4.35)

(4.36)

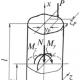
Thus, it is advisable to use the theorem on the change in the angular momentum to study the motion of a rigid body, which is very widespread in technology, and its rotation around a fixed axis.

The law of conservation of the angular momentum of the system

1. Let in expression (4.32).

Then it follows from equation (4.32) that, i.e. if the sum of the moments of all external forces applied to the system relative to a given center is equal to zero, then the kinetic moment of the system relative to this center will be numerically and will be constant in direction.

2. If, then. Thus, if the sum of the moments of external forces acting on the system relative to a certain axis is equal to zero, then the angular momentum of the system relative to this axis will be constant.

These results express the law of conservation of angular momentum.

In the case of a rotating rigid body, equality (4.34) implies that, if, then. From here we come to the following conclusions:

If the system is unchangeable (absolutely rigid body), then, consequently, the rigid body also rotates around a fixed axis with a constant angular velocity.

If the system is changeable, then. With increasing (then individual elements of the system move away from the axis of rotation), the angular velocity decreases, because , and with a decrease, it increases, thus, in the case of a variable system, using internal forces, it is possible to change the angular velocity.

The second problem D2 of the test work is devoted to the theorem on the change in the angular momentum of the system relative to the axis.

Problem D2

A uniform horizontal platform (round with radius R or rectangular with sides R and 2R, where R = 1.2 m) with a mass of kg rotates with angular velocity around the vertical axis z, spaced from the center of mass C of the platform at a distance OC = b (Fig. D2.0 - D2.9, table.D2); dimensions for all rectangular platforms are shown in fig. D2.0a (top view).

At the moment of time, a load D with a mass of kg begins to move along the platform chute (under the action of internal forces) according to the law, where s is expressed in meters, t - in seconds. Simultaneously, a pair of forces begins to act on the platforms with the moment M (given in newtonometers; for M< 0 его направление противоположно показанному на рисунках).

Determine, neglecting the mass of the shaft, the dependence, i.e. the angular velocity of the platform as a function of time.

In all the figures, the load D is shown in the position at which s> 0 (when s< 0, груз находится по другую сторону от точки А). Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии OC = b от центра C.

Directions. Problem D2 - on the application of the theorem on the change in the angular momentum of the system. When applying the theorem to a system consisting of a platform and a load, the kinetic moment of the system relative to the z axis is determined as the sum of the moments of the platform and the load. It should be borne in mind that the absolute speed of the cargo is the sum of the relative and portable speeds, i.e. ... Therefore, the amount of movement of this cargo ... Then you can use Varignon's theorem (statics), according to which; these moments are calculated in the same way as the moments of forces. The course of the solution is explained in more detail in example D2.

When solving the problem, it is useful to depict in the auxiliary drawing a view of the platform from above (from the end z), as is done in Fig. D2.0, a - D2.9, a.

The moment of inertia of a plate with mass m relative to the Cz axis, perpendicular to the plate and passing through its center of mass, is: for a rectangular plate with sides and

;

For round insert of radius R

Example D2... A homogeneous horizontal platform (rectangular with sides 2l and l), which has a mass, is rigidly attached to the vertical shaft and rotates with it around the axis z with angular velocity (Fig.D2a ). At the moment of time, the torque M begins to act on the shaft, directed opposite ; simultaneously cargo D mass in the gutter AB at the point FROM, begins to move along the chute (under the action of internal forces) according to the law s = CD = F (t).

Given: m 1 = 16 kg, t 2= 10 kg, l= 0.5 m, = 2, s = 0.4t 2 (s - in meters, t - in seconds), M= kt, Where k= 6 Nm / s. Determine: - the law of change in the angular velocity of the platform.

Decision. Consider a mechanical system consisting of a platform and a load D. To determine w, we apply the theorem on the change in the angular momentum of the system with respect to the axis z:

(1)

Let us represent the external forces acting on the system: the reaction gravity forces and the torque M. Since the forces and are parallel to the z-axis, and the reactions intersect this axis, their moments about the z-axis are equal to zero. Then, assuming the direction for the moment to be positive (i.e., counterclockwise), we obtain and equation (1) will take this form.

Since the mass of a point is constant, and its acceleration, the equation expressing the basic law of dynamics can be represented in the form

The equation simultaneously expresses the theorem on the change in the momentum of a point in differential form: time derivative from the momentum of the point is equal to the geometric sum of the forces acting on the point.

Let's integrate this equation. Let the point of mass m, moving under the action of a force (Fig. 15), has at the moment t= 0 speed, and at the moment t 1 - speed.

Fig. 15

Then we multiply both sides of the equality by and take definite integrals from them. In this case, on the right, where the integration is in time, the limits of the integrals are 0 and t 1, and on the left, where the speed is integrated, the limits of the integral will be the corresponding values ​​of the speed and ... Since the integral of is equal to , then as a result we get:

.

The integrals on the right represent the impulses of the acting forces. Therefore, we will finally have:

.

The equation expresses the theorem about the change in the momentum of a point in its final form: the change in the momentum of a point over a certain period of time is equal to the geometric sum of the impulses of all forces acting on the point during the same period of time ( fig. fifteen).

When solving problems, instead of a vector equation, equations in projections are often used.

In the case of rectilinear motion along the axis Oh the theorem is expressed by the first of these equations.

Self-test questions

Formulate the basic laws of mechanics.

Which equation is called the basic equation of dynamics?

What is the measure of the inertness of solids during translational motion?

Does body weight depend on the location of the body on Earth?

What frame of reference is called inertial?

To which body is the inertial force of a material point applied and what are its modulus and direction?

Explain the difference between the concepts of "inertia" and "force of inertia"?

To which bodies is the inertial force applied, how is it directed and by what formula can it be calculated?

What is the principle of kinetostatics?

What are the modules and directions of tangential and normal forces of inertia of a material point?

What is called body weight? What is the SI unit of mass?

What is the measure of the body's inertia?

Write down the basic law of dynamics in vector and differential form?

A constant force acts on a material point. How does the point move?

What acceleration will a point receive if it is acted upon by a force equal to twice the force of gravity?

After the collision of two material points with masses m 1 = 6 kg and m 2 = 24 kg, the first point received an acceleration of 1.6 m / s. What is the acceleration obtained by the second point?

At what motion of a material point is its tangential force of inertia equal to zero and at what is normal?

What formulas are used to calculate the modules of the rotational and centrifugal forces of inertia of a point belonging to a rigid body rotating around a fixed axis?

How is the basic law of point dynamics formulated?

Give the formulation of the law of independence of the action of forces.

Write down the differential equations of motion of a material point in vector and coordinate form.

Formulate the essence of the first and second main tasks of the point dynamics.

Give the conditions from which the integration constants of the differential equations of motion of a material point are determined.

What equations of dynamics are called natural equations of motion of a material point?

What are the two main problems of the dynamics of a point, which are solved using the differential motions of a material point?

Differential equations of motion of a free material point.

How are the constants determined when integrating the differential equations of motion of a material point?

Determination of the values ​​of arbitrary constants that appear when integrating the differential equations of motion of a material point.

What are the laws of free fall of a body?

What are the laws governing the horizontal and vertical movements of a body thrown at an angle to the horizon in a void? What is the trajectory of its movement and at what angle does the body have the greatest flight range?

How to calculate an impulse of variable force over a finite period of time?

What is called the amount of motion of a material point?

How to express the elementary work of the force through the elementary path of the point of application of the force and how - through the increment of the arc coordinate of this point?

On what displacements is the work of gravity: a) positive, b) negative, c) equal to zero?

How to calculate the power of a force applied to a material point rotating around a fixed axis with angular velocity?

Formulate a theorem about the change in the amount of motion of a material point.

Under what conditions does the momentum of a material point not change? Under what conditions does its projection on a certain axis not change?

Give the formulation of the theorem about the change in the kinetic energy of a material point in differential and finite form.

What is called the angular momentum of a material point relative to: a) center, b) axis?

How is the theorem about the change in the angular momentum of a point relative to the center and relative to the axis formulated?

Under what conditions does the angular momentum of a point about the axis remain unchanged?

How are the moments of angular momentum of a material point relative to the center and relative to the axis determined? What is the relationship between them?

At what location of the vector of the momentum of a material point is its moment relative to the axis equal to zero?

Why does the trajectory of a material point moving under the action of a central force lie in the same plane?

What movement of a point is called straight-line? Write down the differential equation of the rectilinear motion of a material point.

Write down the differential equations of the plane motion of a material point.

What motion of a material point is described by the Lagrange differential equations of the first kind?

In what cases is a material point called non-free and what are the differential equations of motion of this point?

Give definitions of stationary and non-stationary, holonomic and nonholonomic connections.

What kind of connections are called two-way? One-sided?

What is the essence of the principle of freedom from bonds?

What is the form of the differential equations of motion of a non-free material point in the Lagrange form? What is called the Lagrange multiplier?

Give the formulation of the dynamic Coriolis theorem.

What is the essence of the Galileo-Newton principle of relativity?

Name the movements for which the Coriolis force of inertia is zero.

What is the module and what direction do the transport and Coriolis forces of inertia have?

What is the difference between the differential equations of the relative and absolute motions of a material point?

How are the transferable and Coriolis forces of inertia determined in various cases of transferable motion?

What is the essence of the principle of relativity of classical mechanics?

What frames of reference are called inertial?

What is the condition for the relative rest of a material point?

At what points on the earth's surface does gravity have the greatest and least value?

What explains the deviation of falling bodies to the east?

In what direction does a body thrown vertically upward deviate?

A bucket is lowered into the mine with acceleration but= 4 m / s 2. Bucket gravity G= 2 kN. Determine the tensile strength of the rope supporting the bucket?

Two material points move in a straight line at constant speeds of 10 and 100 m / s. Can it be argued that equivalent systems of forces are applied to these points?

1) it is impossible;

The same forces are applied to two material points weighing 5 and 15 kg. Compare the numerical values ​​of the acceleration of these points?

1) the accelerations are the same;

2) the acceleration of a point with a mass of 15 kg is three times less than the acceleration of a point with a mass of 5 kg.

Can dynamic problems be solved using equilibrium equations?

The amount of movement of a material point is called the vector quantity mV, equal to the product of the mass of a point by the vector of its velocity. Vector mV attached to a moving point.

The amount of movement of the system is called the vector quantity Q equal to the geometric sum (principal vector) of the quantities of motion of all points of the system:

Vector Q is a free vector. In SI units, the momentum modulus is measured in kg m / s or N s.

As a rule, the velocities of all points of the system are different (see, for example, the distribution of the velocities of the points of a rolling wheel shown in Fig. 6.21), and therefore direct summation of the vectors on the right-hand side of equality (17.2) is difficult. Let us find a formula with which the value Q it is much easier to calculate. It follows from equality (16.4) that

Taking the time derivative from both sides, we get Hence, taking into account equality (17.2), we find that

that is, the momentum of the system is equal to the product of the mass of the entire system by the speed of its center of mass.

Note that the vector Q, like the main vector of forces in statics, it is some generalized vector characteristic of the motion of the entire mechanical system. In the general case of movement of the system, its momentum Q can be considered as a characteristic of the translational part of the motion of the system together with its center of mass. If during the movement of the system (body) the center of mass is motionless, then the momentum of the system will be equal to zero. Such, for example, is the amount of motion of a body rotating around a fixed axis passing through its center of mass.

Example. Determine the amount of movement of the mechanical system (Fig.17.1, but), consisting of cargo BUT mass t A - 2 kg, homogeneous block IN weighing 1 kg and wheels D mass m D - 4 kg. Cargo BUT moves with speed V A - 2 m / s, wheel D rolls without slipping, the thread is inextensible and weightless. Decision. The amount of movement of the system of bodies

Body BUT moves progressively and Q A = m A V A(numerically Q A= 4 kg m / s, vector direction Q A coincides with the direction V A). Block IN makes a rotational movement around a fixed axis passing through its center of mass; hence, Q B - 0. Wheel D performs a plane-parallel

traffic; its instantaneous center of velocities is at the point TO, therefore, the speed of its center of mass (points E) is equal to V E = V A / 2 = 1 m / s. Wheel movement amount Q D - m D V E - 4 kg m / s; vector Q D directed horizontally to the left.

By drawing vectors Q A and Q D in fig. 17.1, b, we find the amount of motion Q systems according to formula (a). Taking into account the directions and numerical values ​​of the quantities, we get Q ~ ^ Q A + Q E= 4l / 2 ~ kg m / s, vector direction Q shown in fig. 17.1, b.

Considering that a -dV / dt, equation (13.4) of the basic law of dynamics can be represented as

Equation (17.4) expresses the theorem on the change in the momentum of a point in differential form: at each moment in time, the time derivative of the momentum of a point is equal to the force acting on the point. (In essence, this is another formulation of the basic law of dynamics, close to the one given by Newton.) If several forces act on a point, then on the right side of equality (17.4) there will be a resultant of forces applied to a material point.

If both sides of the equality are multiplied by dt, we get

The vector quantity on the right side of this equality characterizes the action exerted on the body by the force for an elementary period of time dt this value is denoted dS and called an elementary impulse of force, i.e.

Pulse S strength F over a finite time interval /, - / 0 is defined as the limit of the integral sum of the corresponding elementary impulses, i.e.

In a particular case, if the force F constant modulo and direction, then S = F (t| - / 0) and S- F (t l -/ 0). In the general case, the modulus of a force impulse can be calculated from its projections onto the coordinate axes:

Now, integrating both sides of equality (17.5) for t= const, we get

Equation (17.9) expresses the theorem on the change in the momentum of a point in the final (integral) form: the change in the momentum of a point over a certain period of time is equal to the impulse of the force acting on the point (or the impulse of the resultant of all forces applied to it) for the same period of time.

When solving problems, the equations of this theorem are used in projections on the coordinate axes

Now consider a mechanical system consisting of P material points. Then, for each point, the theorem on the change in the momentum in the form (17.4) can be applied, taking into account the external and internal forces applied to the points:

Summing these equalities and taking into account that the sum of the derivatives is equal to the derivative of the sum, we obtain

Since by the property of internal forces HF k= 0 and by definition of the amount of motion ^ fn k V / c = Q, then we finally find

Equation (17.11) expresses the theorem on the change in the momentum of the system in differential form: at each moment of time, the time derivative of the momentum of the system is equal to the geometric sum of all external forces acting on the system.

Projecting equality (17.11) onto the coordinate axes, we obtain

Multiplying both sides of (17.11) by dt and integrating, we get

where 0, Q 0 - the momentum of the system at the moments of time, respectively, and / 0.

Equation (17.13) expresses the theorem on the change in the momentum of the system in integral form: the change in the momentum of the system for any time is equal to the sum of the impulses of all external forces acting on the system during the same time.

In projections onto the coordinate axes, we obtain

From the theorem on the change in the momentum of the system, the following important consequences can be obtained, which express the law of conservation of the momentum of the system.

• 1. If the geometric ^ umma of all external forces acting on the system is zero (LF k= 0), then it follows from equation (17.11) that in this case Q= const, i.e. the vector of the momentum of the system will be constant in magnitude and direction.
• 2. If the external forces acting on the system are such that the sum of their projections onto any axis is zero (for example, I e kx = 0), then it follows from equations (17.12) that in this case Q x = const, that is, the projection of the momentum of the system on this axis remains unchanged.

Note that the internal forces of the system do not participate in the equation of the theorem about the change in the momentum of the system. These forces, although they affect the amount of movement of individual points of the system, cannot change the amount of movement of the system as a whole. Taking this circumstance into account, when solving problems, it is advisable to choose the system under consideration so that unknown forces (all or part of them) are made internal.

The law of conservation of momentum is convenient to apply in cases when the speed of another part of the system must be determined from the change in the speed of one part of the system.

Task 17.1. TO trolley weight t x- 12 kg moving on a smooth horizontal plane at a point BUT a weightless rod is attached using a cylindrical hinge AD length / = 0.6 m with load D mass t 2 - 6 kg at the end (fig.17.2). At the moment of time / 0 = 0, when the trolley speed and () - 0.5 m / s, rod AD starts to rotate around the axis BUT, perpendicular to the plane of the drawing, according to the law φ = (m / 6) (3 ^ 2 - 1) rad (/ -in seconds). Define: u = f.

§ 17.3. The theorem on the motion of the center of mass

The theorem on the change in the momentum of a mechanical system can be expressed in another form, which is called the theorem on the motion of the center of mass.

Substituting into equation (17.11) the equality Q = MV C, get

If the mass M system is constant, then we get

Where and with - acceleration of the center of mass of the system.

Equation (17.15) expresses the theorem on the motion of the center of mass of the system: the product of the system's mass by the acceleration of its center of mass is equal to the geometric sum of all external forces acting on the system.

Projecting equality (17.15) onto the coordinate axes, we obtain

Where x c, y c, z c - coordinates of the center of mass of the system.

These equations are differential equations of motion of the center of mass in projections on the axis of the Cartesian coordinate system.

Let us discuss the results obtained. Let us first recall that the center of mass of the system is a geometrical point, sometimes located outside the geometrical boundaries of the body. The forces acting on the mechanical system (external and internal) are applied to all material points of the system. Equations (17.15) make it possible to determine the motion of the center of mass of the system without determining the motion of its individual points. Comparing equations (17.15) of the theorem on the motion of the center of mass and equations (13.5) of Newton's second law for a material point, we come to the conclusion: the center of mass of a mechanical system moves like a material point, the mass of which is equal to the mass of the entire system, and as if all external forces acting on the system are applied to this point. Thus, the solutions that we obtain, considering this body as a material point, determine the law of motion of the center of mass of this body.

In particular, if the body is moving translationally, then the kinematic characteristics of all points of the body and its center of mass are the same. therefore a translationally moving body can always be regarded as a material point with a mass equal to the mass of the whole body.

As can be seen from (17.15), the internal forces acting on the points of the system do not affect the motion of the center of mass of the system. Internal forces can affect the movement of the center of mass in cases where external forces change under their influence. Examples of this will be given below.

From the theorem on the motion of the center of mass, the following important consequences can be obtained, which express the conservation law of the motion of the center of mass of the system.

1. If the geometric sum of all external forces acting on the system is zero (LF k= 0), then from equation (17.15) it follows that

that at the same time and c = 0 or V c = const, i.e., the center of mass of this system

moves at a speed constant in absolute value and direction (otherwise, uniformly and rectilinearly). In a particular case, if at first the center of mass was at rest ( V c= 0), then he will remain at rest; from where

track he knows that his position in space will not change, that is, r c = const.

2. If the external forces acting on the system are such that the sum of their projections onto some axis (for example, the axis x) is zero (? F e kx= 0), then it follows from equation (17.16) that in this case x with= 0 or V Cx = x c = const, that is, the projection of the velocity of the center of mass of the system onto this axis is a constant value. In a particular case, if at the initial moment Vex= 0, then at any subsequent moment of time this value will be preserved, and from this it follows that the coordinate x with the center of mass of the system will not change, i.e. x c - const.

Let's consider examples illustrating the law of motion of the center of mass.

Examples. 1. As noted, the movement of the center of mass depends only on external forces; it is impossible to change the position of the center of mass by internal forces. But the internal forces of the system can cause external influences. So, the movement of a person on a horizontal surface occurs under the action of frictional forces between the soles of his shoes and the road surface. The force of his muscles (internal forces) pushes a person with his feet from the surface of the road, which is why a friction force (external for a person) arises at the points of contact with the road, directed in the direction of his movement.

• 2. The car moves in the same way. Internal pressure forces in its engine make the wheels rotate, but since the latter have adhesion to the road, the resulting friction forces "push" the car forward (as a result, the wheels do not rotate, but move in a plane-parallel manner). If the road is absolutely smooth, then the center of mass of the car will be stationary (at zero initial speed) and the wheels, in the absence of friction, will slip, that is, make a rotational motion.
• 3. Movement with the help of a propeller, propeller, oars occurs due to the rejection of a certain mass of air (or water). If we consider the discarded mass and the moving body as one system, then the forces of interaction between them, as internal, cannot change the total amount of motion of this system. However, each of the parts of this system will move, for example, the boat forward, and the water, which is thrown by the oars, backward.
• 4. In an airless space, when the rocket moves, the "discarded mass" should be "taken with you": the jet engine imparts motion to the rocket by throwing back the combustion products of the fuel with which the rocket is fueled.
• 5. When descending by parachute, it is possible to control the movement of the center of mass of the man-parachute system. If, with muscular efforts, a person pulls the parachute lines so that the shape of his canopy or the angle of attack of the air flow changes, this will cause a change in the external influence of the air flow, and thereby influence the movement of the entire system.

Task 17.2. IN To task 17.1 (see fig. 17.2) determine: 1) trolley motion law x (= /) (/) if it is known that at the initial moment of time t 0 = The system was at rest and the coordinate x 10 = 0; 2) ^ the law of the change with time of the total value of the normal reaction N (N = N "+ N") horizontal plane, i.e. N = f 2 (t).

Decision. Here, as in Problem 17.1, consider a system consisting of a cart and a load D, in an arbitrary position under the action of external forces applied to it (see Fig. 17.2). Coordinate Axes Ooh draw so that the x axis is horizontal, and the axis at passed through the point A 0, i.e. the location of the point BUT at the moment t-t 0 - 0.

1. Determination of the law of motion of the trolley. To determine x, = /, (0, we use the theorem on the motion of the center of mass of the system. Let us compose the differential equation of its motion in projection onto the x axis:

Since all external forces are vertical, then T, F e kx = 0, and therefore

Integrating this equation, we find that Mx c = B, that is, the projection of the velocity of the center of mass of the system onto the x-axis is a constant value. Since at the initial moment of time

By integrating the equation Mx c= 0, we get

i.e. coordinate x with the center of mass of the system is constant.

Let's write the expression Mx c for an arbitrary position of the system (see Fig. 17.2), taking into account that x A - x { , x D - x 2 and x 2 - x ( - I sin f. In accordance with formula (16.5), which determines the coordinate of the center of mass of the system, in this case Mx c - t (x ( + t 2 x 2 ".

for an arbitrary moment in time

for the moment of time / () = 0, x (= 0 and

In accordance with equality (b), the coordinate x with the center of mass of the entire system remains unchanged, i.e., xD ^,) = x c (t). Therefore, equating expressions (c) and (d), we obtain the dependence of the x coordinate on time.

Answer: X - 0.2 m, where t - in seconds.

2. Determination of the reaction N. For determining N = f 2 (t) we compose the differential equation of motion of the center of mass of the system in projection onto the vertical axis at(see fig.17.2):

Hence, denoting N = N + N ", get

According to the formula determining the ordinate with the center of mass of the system, Mu s = t (y x + m 2 y 2, where y, = at C1,at 2= y D = Havebut ~ 1 cos Ф "we get

Differentiating this equality twice in time (taking into account that at C1 and at A values ​​are constant and, therefore, their derivatives are equal to zero), we find

Substituting this expression into equation (e), we determine the desired dependence N from t.

Answer: N- 176,4 + 1,13,

where φ = (π / 6) (3 / -1), t - in seconds, N- in newtons.

Task 17.3. Electric motor mass t x bolted to the horizontal surface of the foundation (fig. 17.3). On the motor shaft at right angles to the axis of rotation, a weightless rod of length / is fixed at one end, at the other end of the rod a point weight is mounted BUT mass t 2. The shaft rotates uniformly with an angular velocity c. Find the horizontal motor pressure on the bolts. Decision. Consider a mechanical system consisting of a motor and a point weight BUT, in an arbitrary position. Let us depict external forces acting on the system: gravity P x, P 2, foundation reaction in the form of vertical force N and horizontal force R. Let's draw the x-axis horizontally.

To determine the horizontal pressure of the motor on the bolts (and it will be numerically equal to the reaction R and directed opposite to the vector R ), we compose the equation of the theorem about the change in the momentum of the system in projection onto the horizontal x-axis:

For the system under consideration in its arbitrary position, given that the momentum of the motor body is zero, we get Q x = - t 2 U A com. Taking into account that V A = a s /, f = w / (the rotation of the motor is uniform), we get Q x - - m 2 co / cos co /. Differentiating Q x in time and substituting into equality (a), we find R- m 2 co 2 / sin co /.

Note that it is precisely such forces that are compelling (see § 14.3), when they act, forced vibrations of structures arise.

Exercises for independent work

• 1. What is called the amount of motion of a point and a mechanical system?
• 2. How does the amount of motion of a point uniformly moving along a circle change?
• 3. What characterizes the impulse of force?
• 4. Do the internal forces of the system affect its momentum? On the movement of its center of mass?
• 5. How do the couples of forces applied to it affect the motion of the center of mass of the system?
• 6. Under what conditions is the center of mass of the system at rest? moving evenly and in a straight line?

7. In a stationary boat, in the absence of water flow, an adult sits at the stern, and a child sits at the bow of the boat. Which direction will the boat move if they swap places?

In which case the module for moving the boat will be large: 1) if the child moves to the adult at the stern; 2) if an adult goes to a child on the bow of the boat? What will be the displacements of the center of mass of the "boat and two people" system during these movements?

Differential equation of motion of a material point under the action of force F can be represented in the following vector form:

Since the mass of the point m is accepted constant, then it can be entered under the sign of the derivative. Then

Formula (1) expresses the theorem on the change in the momentum of a point in differential form: the first time derivative of the momentum of the point is equal to the force acting on the point.

In projections on the coordinate axes (1) can be represented as

If both sides of (1) are multiplied by dt, then we get another form of the same theorem - the impulse theorem in differential form:

those. the differential of the momentum of the point is equal to the elementary impulse of the force acting on the point.

Projecting both sides of (2) onto the coordinate axes, we obtain

Integrating both sides of (2) within the range from zero to t (Fig. 1), we have

where is the speed of the point at the moment t; - speed at t = 0;

S- impulse of power over time t.

Expression in the form (3) is often called the momentum theorem in the final (or integral) form: the change in the momentum of a point over any period of time is equal to the impulse of force over the same period of time.

In projections onto the coordinate axes, this theorem can be represented as follows:

For a material point, the theorem on the change in the momentum in any of the forms, in essence, does not differ from the differential equations of motion of a point.

The theorem on the change in the amount of motion of the system

The quantity of motion of the system is the vector quantity Q equal to the geometric sum (principal vector) of the quantities of motion of all points of the system.

Consider a system consisting of n material points. Let us compose the differential equations of motion for this system and add them term by term. Then we get:

The last sum is equal to zero by the property of internal forces. Moreover,

We finally find:

Equation (4) expresses the theorem on the change in the momentum of the system in differential form: the time derivative of the momentum of the system is equal to the geometric sum of all external forces acting on the system.

Let's find another expression of the theorem. Let at the moment t= 0 the amount of movement of the system is Q 0, and at the moment of time t 1 becomes equal Q 1. Then, multiplying both sides of equality (4) by dt and integrating, we get:

Or, where:

(S- impulse of force)

since the integrals on the right give impulses of external forces,

equation (5) expresses the theorem on the change in the momentum of the system in integral form: the change in the momentum of the system over a certain period of time is equal to the sum of impulses of external forces acting on the system over the same period of time.

In projections on the coordinate axes, we will have:

The law of conservation of momentum

From the theorem on the change in the momentum of the system, the following important consequences can be obtained:

1. Let the sum of all external forces acting on the system be equal to zero:

Then it follows from Eq. (4) that in this case Q = const.

In this way, if the sum of all external forces acting on the system is equal to zero, then the vector of the momentum of the system will be constant in 10 modulus and direction.

2.01 Let the external forces acting on the system be such that the sum of their projections onto some axis (for example, Ox) is equal to zero:

Then it follows from Eqs. (4 ') that in this case Q = const.

In this way, if the sum of the projections of all external forces acting on some axis is equal to zero, then the projection of the momentum of the system on this axis is a constant value.

These results express the law of conservation of the momentum of the system. It follows from them that internal forces cannot change the total momentum of the system.

Let's look at some examples:

· I feel about it. If we consider the rifle and the bullet as one system, then the pressure of the powder gases when fired will be an internal force. This force cannot change the total amount of motion of the system. But since the propellant gases, acting on the bullet, impart a certain amount of forward movement to it, they must simultaneously impart the same amount of movement to the rifle in the opposite direction. This will cause the rifle to move backward, i.e. the so-called recoil. A similar phenomenon occurs when firing a gun (rollback).

· Work about t and grebn about in and n and (propeller). The screw imparts motion to a certain mass of air (or water) along the axis of the screw, throwing this mass back. If we consider the discarded mass and the aircraft (or ship) as one system, then the forces of interaction between the propeller and the medium as internal cannot change the total momentum of this system. Therefore, when throwing a mass of air (water) backward, the aircraft (or ship) obtains the corresponding forward speed, such that the total momentum of the system under consideration remains equal to zero, since it was zero before the start of movement.

A similar effect is achieved by the action of oars or paddle wheels.

· Reacting. In a rocket (rocket), gaseous products of fuel combustion are ejected at high speed from the hole in the tail of the rocket (from the jet engine nozzle). The pressure forces acting in this case will be internal forces and they cannot change the total momentum of the rocket-propellant gases system. But since the escaping gases have a certain amount of motion directed backward, the rocket receives a corresponding forward speed.

Axis moment theorem.

Consider a material point of mass m moving by force F... Let us find for it the relationship between the angular momentum of the vectors mV and F relative to some fixed Z-axis.

m z (F) = xF - уF (7)

Similarly for the quantity m (mV) if you take out m the parenthesis will be

m z (mV) = m (xV - yV)(7`)

Taking the time derivatives of both sides of this equality, we find

On the right side of the resulting expression, the first parenthesis is 0, since dx / dt = V and dу / dt = V, the second parenthesis according to formula (7) is equal to

m z (F), since according to the basic law of dynamics:

Finally, we will have (8)

The resulting equation expresses the theorem of moments about the axis: the time derivative of the angular momentum of a point relative to some axis is equal to the moment of the acting force relative to the same axis. A similar theorem also holds for the moments relative to any center O.

Any mechanical system consisting of any bodies can act as a system, which is discussed in the theorem.

Statement of the theorem

The quantity of motion (impulse) of a mechanical system is called a quantity equal to the sum of the quantities of motion (impulses) of all bodies included in the system. The impulse of external forces acting on the bodies of the system is the sum of the impulses of all external forces acting on the bodies of the system.

( kg m / s)

The theorem on the change in the amount of motion of the system states

The change in the momentum of the system over a certain period of time is equal to the impulse of external forces acting on the system for the same period of time.

The law of conservation of momentum of the system

If the sum of all external forces acting on the system is zero, then the momentum (momentum) of the system is a constant value.

, we obtain the expression of the theorem about the change in the momentum of the system in differential form:

Integrating both sides of the resulting equality over an arbitrary time interval between some and, we obtain the expression of the theorem about the change in the momentum of the system in integral form:

Impulse conservation law (The law of conservation of momentum) asserts that the vector sum of the momenta of all bodies in the system is a constant value if the vector sum of the external forces acting on the system is equal to zero.

(moment of movement m 2 kg s −1)

The theorem on the change in the angular momentum about the center

the time derivative of the angular momentum (angular momentum) of a material point relative to some fixed center is equal to the moment of the force acting on the point relative to the same center.

dk 0 /dt = M 0 (F ) .

The theorem on the change in the angular momentum about the axis

the time derivative of the angular momentum (angular momentum) of a material point relative to any fixed axis is equal to the moment of the force acting on this point relative to the same axis.

dk x /dt = M x (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) .

Consider a material point M mass m moving under the action of force F (Figure 3.1). Let's write down and construct the vector of angular momentum (angular momentum) M 0 material point relative to the center O :

We differentiate the expression of the angular momentum (angular momentum k 0) by time:

As dr /dt = V , then the cross product V ⊗ m ⋅ V (collinear vectors V and m ⋅ V ) is equal to zero. In the same time d (m ⋅ V) /dt = F according to the theorem about the momentum of a material point. Therefore, we get that

dk 0 /dt = r ⊗F , (3.3)

Where r ⊗F = M 0 (F ) - vector-moment of force F relatively fixed center O ... Vector k 0 ⊥ plane ( r , m ⊗V ), and the vector M 0 (F ) ⊥ plane ( r ,F ), we finally have

dk 0 /dt = M 0 (F ) . (3.4)

Equation (3.4) expresses the theorem on the change in the angular momentum (angular momentum) of a material point relative to the center: the time derivative of the angular momentum (angular momentum) of a material point relative to some fixed center is equal to the moment of the force acting on the point relative to the same center.

Projecting equality (3.4) on the Cartesian coordinate axis, we obtain

dk x /dt = M x (F ); dk y /dt = M y (F ); dk z /dt = M z (F ) . (3.5)

Equalities (3.5) express the theorem on the change in the angular momentum (angular momentum) of a material point relative to the axis: the time derivative of the angular momentum (angular momentum) of a material point relative to any fixed axis is equal to the moment of the force acting on this point relative to the same axis.

Consider the consequences following from Theorems (3.4) and (3.5).

Corollary 1. Consider the case where the force F during the entire movement of the point passes through the fixed center O (the case of a central force), i.e. when M 0 (F ) = 0. Then it follows from Theorem (3.4) that k 0 = const ,

those. in the case of a central force, the angular momentum (angular momentum) of a material point relative to the center of this force remains constant in magnitude and direction (Figure 3.2).

Figure 3.2

From the condition k 0 = const it follows that the trajectory of a moving point is a plane curve, the plane of which passes through the center of this force.

Corollary 2. Let be M z (F ) = 0, i.e. force crosses axis z or is parallel to it. In this case, as can be seen from the third of equations (3.5), k z = const ,

those. if the moment of the force acting on a point relative to any fixed axis is always zero, then the angular momentum (angular momentum) of the point relative to this axis remains constant.

Proof of the theorem on the change in momentum

Let the system consist of material points with masses and accelerations. All forces acting on the bodies of the system can be divided into two types:

External forces are forces acting from bodies that are not part of the system under consideration. The resultant external forces acting on the material point with the number i denote.

Internal forces are the forces with which the bodies of the system itself interact with each other. The force with which to the point with the number i dot with number is in effect k, we will denote, and the force of action i-th point on k th point -. Obviously, for, then

Using the introduced designations, we write Newton's second law for each of the considered material points in the form

Considering that and summing up all the equations of Newton's second law, we get:

The expression is the sum of all internal forces acting in the system. According to Newton's third law, in this sum, each force corresponds to a force such that, therefore, it is fulfilled Since the entire sum consists of such pairs, then the sum itself is equal to zero. Thus, one can write

Using the notation for the momentum of the system, we obtain

Introducing into consideration the change in the impulse of external forces , we obtain the expression of the theorem about the change in the momentum of the system in differential form:

Thus, each of the last obtained equations allows us to assert: the change in the momentum of the system occurs only as a result of the action of external forces, and internal forces cannot exert any influence on this value.

Having integrated both sides of the obtained equality over an arbitrarily taken time interval between some and, we obtain the expression of the theorem about the change in the momentum of the system in integral form:

where and are the values ​​of the momentum of the system at moments of time and, respectively, and is the impulse of external forces over a period of time. In accordance with the above and the introduced designations,